8月14小练

网址：CSUST-8-14-小练

这次的题目我只出了一道:A,Teilwal出3道：B,C,D，从此不再 出一道:E

表示我出的题目不是很难，但是很容易出错......因为测试数据太简单......表示我在这边错了一次，在HDU提交了4次才过，错了3次啊......T^T,我的正确率啊......QAQ

A 贪心orDP，B,C 博弈，D 数论 E Dijkstra + 记忆化搜索

A   Doing Homework again  HDU 1789

大意是，要尽可能的少扣学分，要在截止日期之前做完，就不会扣，一个课程有一个截止日期以及他的学分，问最少扣的学分是多少。

代码：     46ms

#include <stdio.h>
#include <iostream>
#include <algorithm>
using namespace std;
class A
{
public:
    int a;
    int b;
}x[1005];
int cmp(A i,A j)
{
    if(i.a==j.a)            //按时间排，时间一样，就学分多的放前面
        return i.b>j.b;
    else
        return i.a<j.a;
}
int main()
{
    int T,n,min,sum,j,k,i,c[1005];
    scanf("%d",&T);
    while(T--)
    {
        sum=0;
        min=1000000;
        scanf("%d",&n);
        for(i=1;i<=n;i++)
        {
            scanf("%d",&x[i].a);
            c[i]=0;
        }
        for(i=1;i<=n;i++)
            scanf("%d",&x[i].b);
        sort(x+1,x+n+1,cmp);    //排序
        k=0;                //选定的个数      
        for(i=1;i<=n;i++)
        {
            if(x[i].a>k)
               {
                c[i]=1;    //已被选定，标记
                k++;
               }
            else   //因为时间原因，没有被选   
            {
                min=x[i].b;
                j=i;
                for(int l=i-1;l>0;l--)    
                    if(c[l]==1&&x[l].b<min)     //在前面被选定的中找到最小的交换
                    {
                        min=x[l].b;
                        j=l;
                    }
                sum+=x[j].b;      //加上这个被换下来的最小的数
                x[j].b=x[i].b;     //交换
            }
        }
        printf("%d
",sum);
    }
    return 0;
}

再来个学姐的代码：                       31ms

觉得学姐的代码好神奇........QAQ   ......我肿么就没想到呢.....

#include <stdio.h>
#include <math.h>
#include <string.h>
#include <algorithm>
#include <iostream>
using namespace std;
const int maxn=1000+10;
int used[maxn];
struct node
{
    int d;
    int s;
}p[maxn];
bool cmp(node a,node b)
{
    return a.s>b.s||(a.s==b.s&&a.d>b.d);     //按学分排序，学分相同就时间大的放前面
}
int main()
{ 
    int T,i,j,n,ans;
    scanf("%d",&T);
    while(T--)
  {
    scanf("%d",&n);
    for(i=1;i<=n;i++)
        scanf("%d",&p[i].d);
    for(i=1;i<=n;i++)
        scanf("%d",&p[i].s);
    sort(p+1,p+1+n,cmp);
    memset(used,0,sizeof(used));
    ans=0;
    for(i=1;i<=n;i++)
    {
        for(j=p[i].d;j>0;j--)
            if(used[j]==0)
            { 
                used[j]=1;    //表示第j天已经有作业了
                break;
            }
        if(j==0)   
           ans+=p[i].s;
    }
    printf("%d
",ans);
 }
return 0;
}

B  Brave Game    HDU 1846

一堆n个石子，每人每次最多取m个，最少取1个，问是先手赢还是后手赢~~~~(≧▽≦)/~

巴什博弈，一个人拿1～m个，那谁面对m+1的局势的的时候则必败，很明显，先拿的就是要造这个局势,如果n是(m+1)*r+s(k为任意，s<m+1),那么很明显先拿的拿掉s后，然后无论下一个拿多少你都可以保证你拿完后都是拿了m+1个，这样后拿的必定面对必败局势，比如23 2，23=（3×7）+2；那我第一次拿掉2，然后无论每次第二个拿几我都可以使得这轮总共拿3，然后他必定会面对3这个局势，然后我就必胜，那什么时候必败呢，很明显如果我面对的是（m+1）的倍数的局势就必败。

所以：代码：    0ms

#include <stdio.h>
int main()
{
    int n,m;
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&m);
        if(n%(m+1) == 0)
                printf("second
");
        else 
                printf("first
");
    }
    return 0;
}

C  取石子游戏    HDU 1527 

详情解释.......来自：http://www.cnblogs.com/jiangjun/archive/2012/10/25/2740194.html

大致上是这样的：有两堆石子，不妨先认为一堆有10，另一堆有15个，双方轮流取走一些石子，合法的取法有如下两种：

1)在一堆石子中取走任意多颗；

2)在两堆石子中取走相同多的任意颗；

约定取走最后一颗石子的人为赢家，求必败态(必胜策略)。

这个可以说是MR.Wythoff(Wythoff于1907年提出此游戏)一生全部的贡献吧，我在一篇日志里就说完有点残酷。这个问题好像被用作编程竞赛的题目，网上有很多把它Label为POJ1067，不过如果学编程的人不知道Beatty定理和Beatty序列 ，他们所做的只能是找规律而已。不熟悉的人可以先在这里 玩几局~

简单分析一下，容易知道两堆石头地位是一样的，我们用余下的石子数(a,b)来表示状态，并画在平面直角坐标系上。

用之前的定理： 有限个结点的无回路有向图有唯一的核  中所述的方法寻找必败态。先标出(0,0)，然后划去所有(0,k),(k,0),(k,k)的格点；然后找y=x上方未被划去的格点，标出(1,2)，然后划去(1,k),(k,2),(1+k,2+k)，同时标出对称点(2,1)，划去(2,k),(1,k),(2+k,1+k)；然后在未被划去的点中在y=x上方再找出(3,5)。。。按照这样的方法做下去，如果只列出a<=b的必败态的话，前面的一些是(0,0),(1,2),(3,5),(4,7),(6,10),…

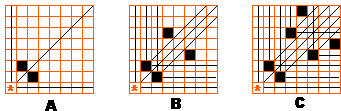
接下来就是找规律的过程了，忽略(0,0)，记第n组必败态为(a[n],b[n])

命题一：a[n+1]=前n组必败态中未出现过的最小正整数

[分析]：如果a[n+1]不是未出现的数中最小的，那么可以从a[n+1]的状态走到一个使a[n+1]更小的状态，和我们的寻找方法矛盾。

命题二：b[n]=a[n]+n

[分析]：归纳法：若前k个必败态分别为 ，下证：第k+1个必败态为

从该第k+1个必败态出发，一共可能走向三类状态，从左边堆拿走一些，从右边堆拿走一些，或者从两堆中拿走一些．下面证明这三类都是胜态．

情况一：由命题一，任意一个比a[k+1]小的数都在之前的必败态中出现过，一旦把左边堆拿少了，我们只要再拿成那个数相应的必败态即可。

情况二（从右边堆拿走不太多）：这使得两堆之间的差变小了，比如拿成了 ，则可再拿成 ；

情况二（从右边堆拿走很多）：使得右边一堆比左边一堆更少，这时类似于情况一，比如拿成了 (其中a[m] ；

情况三：比如拿成 ，则可再拿成 ．

综上所述，任何从 出发走向的状态都可以走回核中．故原命题成立．

以上两个命题对于确定(a[n],b[n])是完备的了，给定(0,0)然后按照这两个命题，就可以写出(1,2),(3,5),(4,7),…

这样我们得到了这个数列的递推式，以下我们把这两个命题当成是(a[n],b[n])的定义。

先证明两个性质：

性质一：核中的a[n],b[n]遍历所有正整数。

[分析]：由命题一，二可得a[n],b[n]是递增的，且由a[n]的定义显然。

性质二：A={a[n]:n=1,2,3,…},B={b[n]:n=1,2,3,…}，则集合A,B不交。

[分析]：由核是内固集，显然。

看到这里大家有没有想到Beatty序列呢，实际上a[n]和b[n]就是一个Beatty序列。

，有 ，解方程

得 ，到此，我们找到了该必败态的通项公式。

实际上这组Beatty序列还有一些别的性质，比如当一个数是Fibonacci数的时候，另一个数也是Fibonacci数；而且两者的比值也越来越接近黄金比，这些性质在得到通项公式之后不难证明。

总的来说，这个问题给我们了哪些启示呢？首先用定理所说的方法找核，然后给出核的规律（递推，或是通项）并且证明。最后附上一张对应的必败态图.

转自http://yjq24.blogbus.com/logs/42653430.html

上次说了胜态和必败态，还记得最后的练习么？桌子上有15个石子，每人每次可以拿去1个或3个石子，拿走最后一个石子的人赢，列出所有的必败态：0,2,4,6,8,10,12,14。说过了状态作为结点可以画一张有向图，下面这张图就是这个游戏所对应的：

 

我只列了不大于6的状态，回顾一下胜态和必败态的性质: 胜态一定可以通过某种策略走向必败态；而必败态采取任何策略都将走向胜态。 用图论的话来说， 因为必败态只能走向胜态，所以任何两个必败态结点之间不可能存在边； 因为胜态总能走到必败态，所以对任何一个非必败态的结点，一定存在一个从它指向必败态结点的边。 不妨看看左图中的0,2,4,6，亲自体会一下。 定义：有向图中，集合X中任意两点之间无边，称集合X为内固集。 定义：有向图中，任意不在集合X中的点存在一条指向集合X的边，称集合X为外固集。 定义：有向图中，集合X 既是外固集，又是内固集，称集合X为核。 显然，内，外固集的定义正好针对上面的两句话，而核就是包含所有必败态的集合。 定理：双人博弈中，约定走最后一步为胜，如果有核存在，则其中一方有不败策略。 证明：不妨设A先行动，初始状态不在核中，由于核是外固集，A一定可以采取某种策略把状态走到核中，然后轮到B；由于核是外固集，所以B不管采取什么策略，都将走出核，所以轮到A的时候，A又可以把状态走进核里。总而言之，A可以使B永远面临核内的状态。无路可走的状态不可能在核外，因为核外总能走到核内，A可以保持不败。如果初始状态不在核中，那么利用同样的想法易知B有不败策略。 以上的定理意义是非凡的，虽然这个定理在证明之前我们其实就已经了解了核与必败态的紧密联系。那么，对一个博弈游戏来说，找出核是核心问题。在此之前，先得考察核得存在性：

定理：有限个结点的无回路有向图有唯一的核。

证明：核可以用如下的方式找出：首先找出没有后继结点的点集P[1]（最基本的必败态，比如上图中的结点0），然后找到那些指向P[1]的结点集合为N[1](最基本的胜态，比如上图的结点1和结点3)；然后，除去P[1]和N[1]中的点并除去和这些点关联的边，继续寻找没有后继结点的点集P[2]（更高级的必败态，比如上图中的结点2），依次类推，则最后的核为P=P[1]并P[2]并…并P[n]。

很容易说明如此找到的核是内固集，也是外固集，满足核的定义，下面说明一下核为什么不是空集：实际上P[1]就不是空集，对一个没有回路的有向图来说，从图上的某一点出发，就无法回到原来到过的点。而图中的点又是有限的，所以最后必将在某个结点终止，故P不是空集。

针对不同的游戏，找核是一个麻烦事。首先生成图，有向边取决于游戏规则，然后当我们要找某个必败态的时候，是要先找到之前所有的必败态的，而这正是一个数学问题和一个编程问题的关键差别。在立方和分解问题[unsolved]中，我的问题的提法都是针对某一个特定输入的n来看是否存在(x,y)满足立方和或者平方和等于n.实际上，如果提法换成，输出对所有不大于n的数中可以被分解的数，那么这种提法更适合计算机去解决，因为本质上来说，两个问题是不一样的。对于前者我只需要知道有关n的情况就可以了，而对后者，却调动了资源去计算所有不大于n的数的情况。虽然他们看起来很相近，但是从道理上来说应该后者的劳动量要大得多，可悲的事情就在于，有时候你要算出n的情况，就不得不算一些比n小的数的情况，而这个计算的数目通常是随着n增大而增大的；另一个可悲的事情是，程序员往往已经习惯了第二种提问方式。数学家希望找到某些必要条件或者充分条件来确定n能否被分解，同样的道理，我们也希望能直接找到必败态的规律，而不真正依赖于象上述定理那样递归的思想从P[1]开始找起，这样来解决问题。

但是，必败态的规律是严格依赖于规则的，这一点对找出必败态的规律来说造成了很大的局限性。这个图的模型在以后还会遇到，到时有更好的方法来寻找必败态。

 转自http://yjq24.blogbus.com/logs/42304551.html

高斯取整函数又叫向下取整函数，常见的记法如下： ，既然是向下取整，也就是说[-3.5]=-4，这个取整对负数来说就不是简单地扔掉小数部分，这是要注意的。可以说,高斯取整是联系连续和离散的重要桥梁。

小知识：高斯函数性质

1) x-1<[x]<=x<[x]+1

2) [x+n]=[x]+n,(n为整数)

3) [x]+[y]<=[x+y]<=[x]+[y]+1 //左边由性质2易证,右边利用[x+y]<=x+y<[x]+[y]+2

4) [nx]>=n[x],(n为正整数) //反复利用性质3左边

5) [x/n]=[[x]/n],(n为正整数)

// 换元后等价于证[ny]/n-1<[y]<=[ny]/n,右边由性质4易证,左边有 [ny]/n<=[y]+{y}<[y]+1

 

欧拉给出过一个很经典的多项式： ，该多项式在n=0,1,2,…,39时产生40个素数。利用高斯取整函数，可以做 一件差不多的事：

，这个函数跳过所有的平方数，而且值域覆盖所有非完全平方数构成的集合，有了上面的这些性质作武器，证明并不难，这里就略去了。

今天的主题还是 Beatty定理 ：

正无理数 满足 ， 则数列 ； 严格递增， 并且这两个数列构成Z+上的一个分划（也就是它们无交地遍历全体正整数）。

[题解]：

其实作为习题是不难的，显然 ，于是 ，故

Step1.先证明两数列不交：[反证]若 ,有 ,即有 ，

两式相加：得k<m+n<k+1，这和m,n,k都是自然数矛盾；

Step2.再证两数列能取遍所有的正整数：[反证]若k不在 中，则有

于是

两式分别除以 和 后相加：得 ,这和m,n,k都为自然数矛盾．

证毕.

由Beatty定理得到的两个数列称为互质数列，不过别被名称所欺骗，a[n]和b[n]并不能保证对应互质。

//再继续看看必败点

一、

      m(k) = k * (1 + sqrt(5))/2

      n(k) = m(k) + k

 二、

 

一个必败点有如下性质：

性质1：所有自然数都会出现在一个必败点中，且仅会出现在一个必败点中；

性质2：规则允许的任意操作可将必败点移动到必胜点；

性质3：一定存在规则允许的某种操作可将必胜点移动到必败点；

 

下面我们证明这3个性质。

 

性质1：所有自然数都会出现在一个必败点中，且仅会出现在一个必败点中；

证明：m(k)是前面没有出现过的最小自然数，自然与前k-1个必败点中的数字都不同；m(k)>m(k-1)，否则违背m(k-1)的选择原则；n(k)=m(k)+k>m(k-1)+(k-1)=n(k-1)>m(k-1)，因此n(k)比以往出现的任何数都大，即也没有出现过。又由于m(k)的选择原则，所有自然数都会出现在某个必败点中。

 

 

性质2：规则允许的任意操作可将必败点移动到必胜点；

证明：以必败点(m(k),n(k))为例。若只改变两个数中的一个，由于性质1，则得到的点一定是必胜点；若同时增加两个数，由于不能改变两数之差，又有n(k)-m(k)=k，故得到的点也一定是必胜点。

 

 

性质3：一定存在规则允许的某种操作可将必胜点移动到必败点；

证明：以某个必胜点(i,j)为例，其中j>i。因为所有自然数都会出现在某个必败点中，故要么i等于m(k)，要么j等于n(k)。

若i=m(k)，j>n(k)，可从j中取走j-n(k)个石子到达必败点；

若i=m(k)，j<n(k)，可从两堆同时拿走m(k)-m(j-m(k))，注意此时j-m(k) < n(k)-m(k) < k，从而到达必败点( m(j-m(k))，m(j-m(k))+j-m(k))；

若i>m(k)，j=n(k)，可从i中取走i-m(k)个石子到达必败点；

若i<m(k)，j=n(k)，需要再分两种情况，因为i一定也出现在某个必败点中，若i=m(l)，则从j中拿走j-n(l)，若i=n(l)，则从j中拿走j-m(l)，从而到达必败点(m(l),n(l))。

 

//看完上面的有了点了解吧，代码如下：

#include<iostream>
#include<cmath>
using namespace std;
int main ()
{
    int a,b,dif;
    double p=(sqrt((double)5)+1)/double(2);
    while(cin>>a>>b)
    {
    dif=abs(a-b);//取差值
    a=a<b?a:b;//取较小的值
    if(a==(int)(p*dif))//判断是不是奇异局势
      printf("0
");
    else printf("1
");
    }
    return 0;
}

 该类问题另一种表述 

 移动的皇后

Problem Description

一个n * n棋盘上有一个皇后。每个人可以把它往左或下或左下45度移动任意多步。把皇后移动至左下角的游戏者获胜。现在给出皇后初始的X坐标和Y坐标，如果轮到你先走，假设双方都采取最好的策略，问最后你是胜者还是败者。

  

Input
输入包含若干行，表示若干种皇后的初始情况，其中每一行包含两个非负整数a和b，表示皇后的初始坐标，a和b都不大于1,000,000,000。

Output
输出对应也有若干行，每行包含一个数字1或0，如果最后你是胜者，则为1，反之，则为0。

Sample Input

2 1
8 4
4 7

Sample Output

0
1
0 

 

 

 

 

C题的代码：      15ms

#include<stdio.h>
#include<math.h>
int main()
{
    double x=(sqrt(5.0)+1)/2;
    int a,b,t;
    while(scanf("%d%d",&a,&b) != EOF)
    {
          if(a>b)
            { 
                t=a;
                a=b; 
                b=t; 
            }
          if(floor(x*(b-a))==a)
            printf("0
");
          else printf("1
");
    }
    return 0;
}

D   Sum      POJ 1844

给出一个数字n，求最小的i，1,2,3......i，数字之间+-都可。

解析：（不是出自我，原作者不详）

* 一：sum一定要大于或等于输入的S.（等于时就已经找到了答案）

*    小于的话就算全做加法运算也不能达到S。

*             

* 二：在满足第一条的情况下，注意一定要满足第一条后

*    第一次碰到（sum　-　S　）　％　２　＝＝　０

*　这里（ sum = 1 + 2  + ....　+　i ）这时的i就是答案。

*  证明如下：

*           1：若res是奇数，就说明res = （ 1 + 2 + ... + i ）- S 是奇数

*         也就是说无论你怎么改变sum（ sum = 1 + 2  + ....　+　i ）表达式

*        （当然是通过改变其中的加号为减号）也无法让res为0

*             举个例子吧:S = 5, sum = 1+2+3 = 6, res = 6 - 5 = 1;

*   无论改变（1+2+3）中的加号也没用，这是因为你在sum中改变一个加号为减号

    时它的值就一定减少了一个偶数值（这是显然的）sum-S仍然为奇数

*        2：令res = sum - S，则res一定是0，2， 4， 6....中的一个

*        下面说明总可以通过改变sum表达式中的某几个加号为减号使得res为0

*          当k = 0的情况就不用说明了吧， 假设2k表示res 显然k = 1 2 3 4...

*            当k = 1 时可以通过把sum（ sum = 1 + 2 + ... + i )

*            改成（ sum = -1 + 2 + ... + i )

*            当k = 2 时可以通过把sum （ sum = 1 + 2 + ... + i )

*            改成( sum = 1 - 2 + ... + i )

*            一次类推res总可以变为0

#include <stdio.h>
#include <iostream>
using namespace std;
int main()
{
    int n,sum,i;
    while(~scanf("%d",&n))
    {
        i=0;
        sum=0;
        while(sum<n || (sum-n)%2==1)
        {
            sum+=++i;
        }
        printf("%d
",i);
    }
    return 0;
}

E   最短路问题   DFS+Dijkstra    A Walk Through the Forest     HDU 1142 

代码：    125MS

#include <iostream>
#include <cstring>
#define N 1010
#define INF 1000000
using namespace std;
int map[N][N],v[N],dis[N],dp[N];
int n,m;
void dij(int start)            //终点到每个点的最短路径（单源最短路径）
{
    int m,x;
    memset(v,0,sizeof(v));
    for(int i=1;i<=n;i++)
        dis[i]=map[start][i];
    dis[start]=0;
    v[start]=1;
    for(int i=1;i<=n;i++)
    {
        m=INF;
        for(int j=1;j<=n;j++)
            if(!v[j]&&dis[j]<m) m=dis[x=j];
        if(m==INF) break;
        v[x]=1;
        for(int j=1;j<=n;j++)
            if(!v[j]&&dis[j]>dis[x]+map[x][j])
            dis[j]=dis[x]+map[x][j];
    }
}
int dfs(int s)
{
    int sum=0;
    if(dp[s]>-1) 
        return dp[s];
    if(s==2) 
        return 1;           //到达终点
    for(int i=1;i<=n;i++)
    {
        if(map[s][i]!=INF&&dis[i]<dis[s])       //s到i有路且s到终点距离大于i到终点的距离   
            sum+=dfs(i);                        //路径条数累加
    }
    dp[s]=sum;
    return dp[s];
}
int main()
{
    int a,b,l;
    while(cin>>n,n)
    {
        cin>>m;
        for(int i=1;i<=n;i++)
         {
            dp[i]=-1;
            for(int j=1;j<=n;j++)
                map[i][j]=INF;               //不存在的边为INF
        }
        while(m--)
        {
            cin>>a>>b>>l;
            map[a][b]=map[b][a]=l;
        }
        dij(2);            //2为终点
        cout<<dfs(1)<<endl;        //从1开始搜

    }
    return 0;
}