题意
长度为n的序列a,要求(1<=ai<=m),且严格先单调递增再单调递减,同时令恰只有一对ai,aj使得ai==aj
给出n,m,求这样的序列的个数,答案对于998244353取模
题解
首先对于每一位都可以成为峰顶,我们枚举峰顶位于第i位
然后我们需要从m个数中选出i个数,对于这选出的个数,我们不妨令为j其中的最大值
此时可以得出

到这里已经可以O(n)求解了,总复杂度O(nlogn),但是还可以继续向下化简
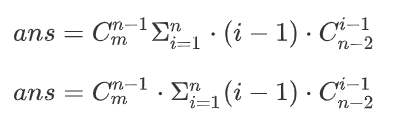
由二项式定理推导(求导)得
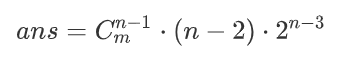
如此可以O(logn)求解,但是预处理还是O(nlogn)
回头再看这个式子的意义
先从m中选出n-1个数
其中最大值肯定为峰顶,再从剩余n-2个数中选出一个数用来重复,剩下n-3个数可以在峰顶左边也可以在峰顶右边,故为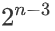
代码
//by 减维 #include<bits/stdc++.h> #define maxn 200005 #define mod 998244353 #define ll long long using namespace std; int n,m; ll ans,fac[maxn],inv[maxn]; ll ksm(ll x,ll y) { ll ret=1; while(y) { if(y&1) ret=ret*x%mod; y>>=1; x=x*x%mod; } return ret; } ll c(ll x,ll y) { if(x<y) return 0; return fac[x]*inv[y]%mod*inv[x-y]%mod; } int main() { scanf("%d%d",&n,&m); fac[0]=inv[0]=1; for(int i=1;i<=m;++i) fac[i]=i*fac[i-1]%mod,inv[i]=ksm(fac[i],mod-2); for(int i=n/2+1;i<=n-1;++i) { int res=n-i; ans=(ans+(n%2&&i==n/2+1?1:2)*fac[n-2]%mod*inv[n-i-1]%mod*inv[i-2]%mod*((c(m,n-1)-c(i-1,n-1)+mod)%mod)%mod)%mod; } printf("%I64d",ans%mod); return 0; }
用到的二项式定理推导过程如下:
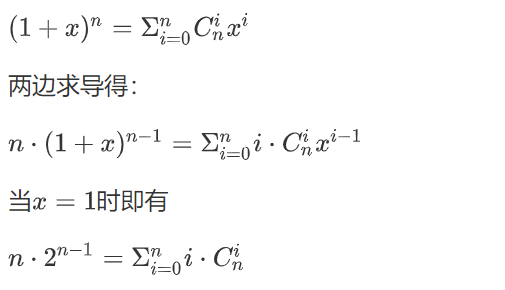
P.S.
我太蠢了比赛的时候各种出错,不过感觉这道题真的挺好的,就算没有第一时间想到也可以慢慢推出来
另外推导过程并不十分严谨