前言:不断学习就是程序员的宿命。---距离2021考研还有101天
目前正在看数据结构---栈,栈有很多应用比如我们IDE的{}、[]这些成对出现的括号匹配问题,假如我们少写一个或多写一个IDE就会帮我们检测出来;又比如中缀表达式的机算(是机算);以及我们熟悉的递归算法中都有栈的身影。下面记录一下用栈来实现中缀表达式的计算
Github代码地址:https://github.com/Simple-Coder/data-structure
一、中缀表达式
举个栗子,((15÷(7-(1+1)))×3)-(2+(1+1)),就是我们熟悉的算术表达式,由3个部分组成:操作数、运算符、界限符。
中缀表达式:a+b,运算符+在操作数ab的中间
后缀表达式(逆波兰式):ab+,运算符在操作数ab的后边
前缀表达式(波兰表达式):+ab,运算符在操作数ab的前边
上述式子我们肉眼手算就知道先进行括号中的运算:先算(1+1)再算(1+1)×3……但是机器可是不知道的!有没有一种表达式可以消除这些括号?于是波兰数学家就贡献给我们:后缀表达式也就是逆波兰表达式,将运算符放在两个操作数后边就消除了这些括号。
二、中缀表达式转后缀表达式(手算)
栗子:A+B*(C/D)-E/F
思想:
①确定中缀表达式中各个运算符的运算顺序(肉眼观察法!)
②选择下一个运算符,按照【左操作数 右操作数 运算符】的方式组合成一个新的操作数
③如果还有运算符没被处理,就继续②
思想有了,呢就操练一把!
手算结果可能有很多种例如:ABCD/*+EF/-

三、后缀表达式的计算(手算)
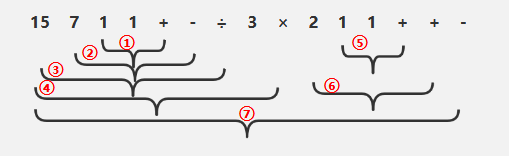
栗子:((15÷(7-(1+1)))×3)-(2+(1+1))转后缀表达式:15 7 1 1 + - ÷ 3 × 2 1 1 + + -
后缀表达式的手算方法:
从左向右扫描,每遇到一个运算符,就让运算符前边最近的两个操作数执行对应运算,合体为一个操作数。(需要主要两个操作数的左右顺序。例如:A÷B与B÷A是不一样的)
四、后缀表达式的计算(机算)
栗子:A+B-C*D/E+F(前缀)--->后缀表达式:AB+CD*E/-F+
用栈来实现后缀表达式的机算:
①从左向右扫描下一个元素,直到处理完所有元素
②若扫描到操作数则压入栈,并回到①;否则执行③
③若扫描到运算符,则依次弹出栈顶2个元素,执行相应运算,运算结果压回栈顶,回到①
思想有了,呢就操练一把!实现如下:
依次扫描后缀表达式:AB+CD*E/-F+
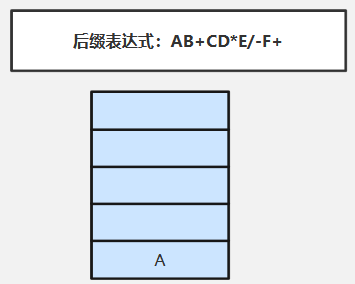
①扫描A(操作数)直接压入栈
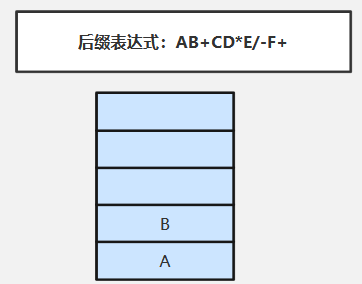
②扫描B(操作数)直接压入栈
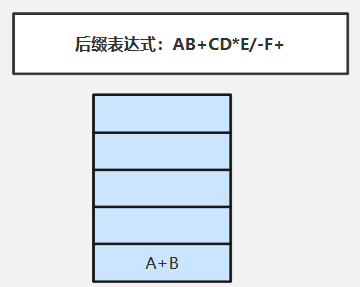
③扫描+(运算符)依次弹出栈顶两个元素B、A(先弹出的B是“右操作数”)执行对应运算:A+B,并将执行结果A+B压入栈中
④扫描C(操作数)直接压入栈
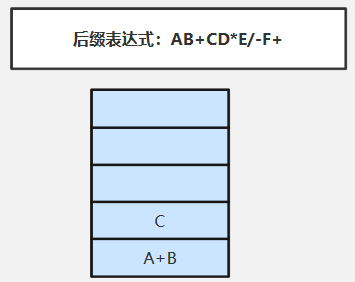
⑤扫描D(操作数)直接压入栈
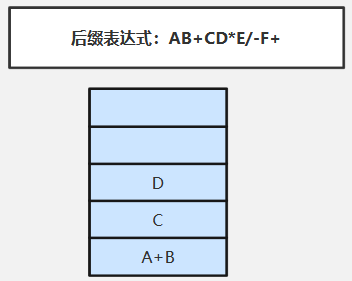
⑥扫描*(运算符)依次弹出栈顶两个元素D、C(先弹出的D是“右操作数”)执行对应运算:C*D,并将执行结果C*D压入栈中
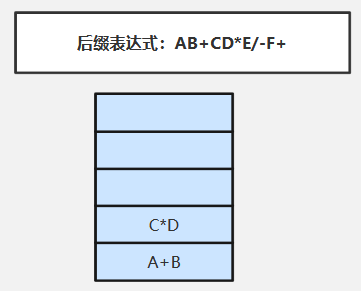
⑦扫描E(操作数)直接压入栈
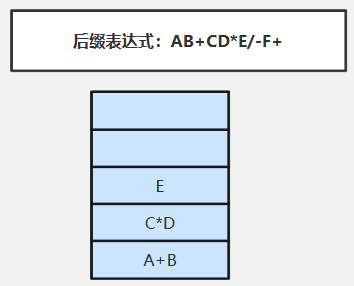
⑧扫描/(运算符)依次弹出栈顶两个元素E、C*D(先弹出的E是“右操作数”)执行对应运算:C*D/E,并将执行结果C*D/E压入栈中
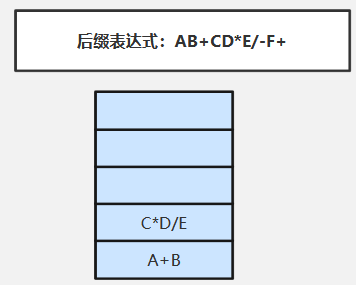
⑨扫描-(运算符)依次弹出栈顶两个元素C*D/E、A+B(先弹出的C*D/E是“右操作数”)执行对应运算:A+B-C*D/E,并将执行结果A+B-C*D/E压入栈中
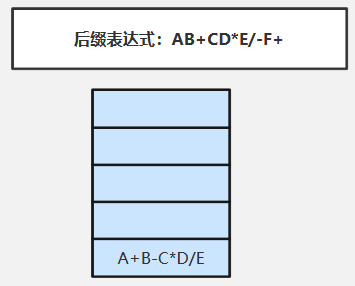
⑩扫描F(操作数)直接压入栈
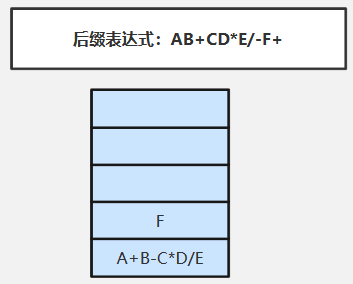
⑪扫描+(运算符)依次弹出栈顶两个元素F、A+B-C*D/E(先弹出的F是“右操作数”)执行对应运算:A+B-C*D/E+F,并将执行结果A+B-C*D/E+F压入栈中

至此所有字符扫描完毕,栈中唯一一个元素为运行结果。
五、中缀转后缀表达式的计算(机算)
思想:初始化一个栈,用于保存暂时还不能确定运算顺序的运算符:
从左向右处理各个元素,直到处理完所有元素,期间可能遇到以下3种情况:
①遇到操作数:直接加入后缀表达式
②遇到界限符:遇到“(”直接入栈;遇到“)”则依次弹出栈内运算符并加入后缀表达式,直到弹出“(”为止。这里需要注意“()”均不加入后缀表达式
③遇到运算符:依次弹出栈中优先级高于或等于当前运算符的所有运算符并加入后缀表达式,若遇到“(”或栈空则停止弹出;最后再将当前运算符压入栈
最后扫描完所有字符后,将栈中剩余元素依次弹出,并加入后缀表达式。
思想有了,呢就操练一把!
1、无界限符转换
例子:A+B-C*D/E+F(中缀表达式)从左向右开始扫描各个元素:
①扫描A(操作数)直接加入后缀表达式:A
②扫描+(运算符):需要依次弹出栈中优先级高于或等于当前运算符(+)的所有运算符加入后缀表达式,若遇到“(”或栈空则停止弹出-------由于栈空则直接退出,最后当前运算符(+)入栈
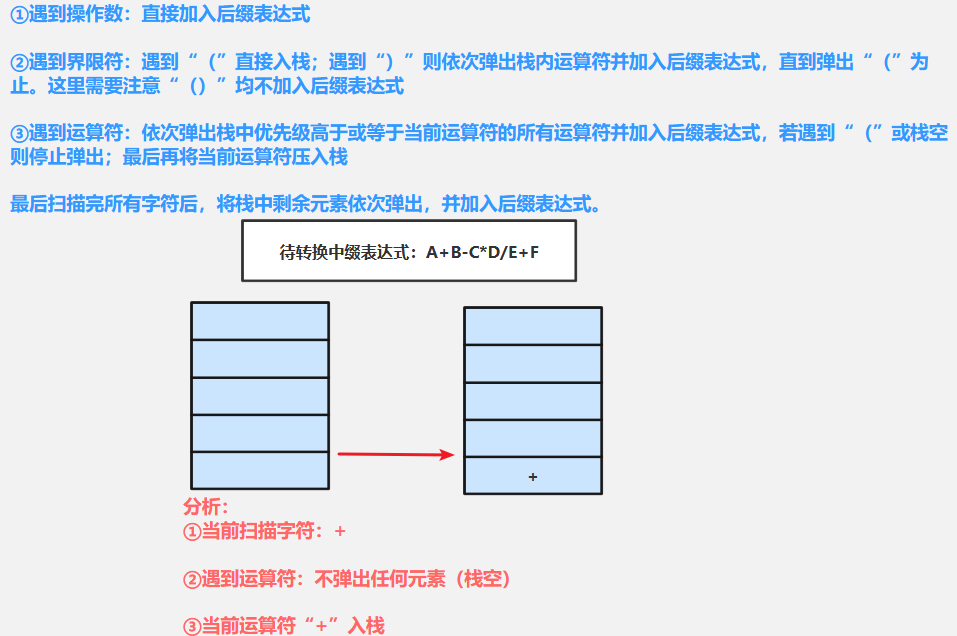
③扫描B(操作数)直接加入后缀表达式:AB
④扫描-(运算符):需要依次弹出栈中优先级高于或等于当前运算符(-)的所有运算符加入后缀表达式,若遇到“(”或栈空则停止弹出--------由于目前栈中有+与当前运算符(-)优先级相等,需要弹出栈中+加入后缀表达式:AB+,最后将当前运算符-压入栈中

⑤扫描C(操作数):直接加入后缀表达式AB+C
⑥扫描*(运算符):需要依次弹出栈中优先级高于或等于当前运算符(*)的所有运算符加入后缀表达式,若遇到“(”或栈空则停止弹出--------由于当前栈中运算符(-)优先级小于当前运算符(*),不再弹出;最后当前运算符(*)入栈
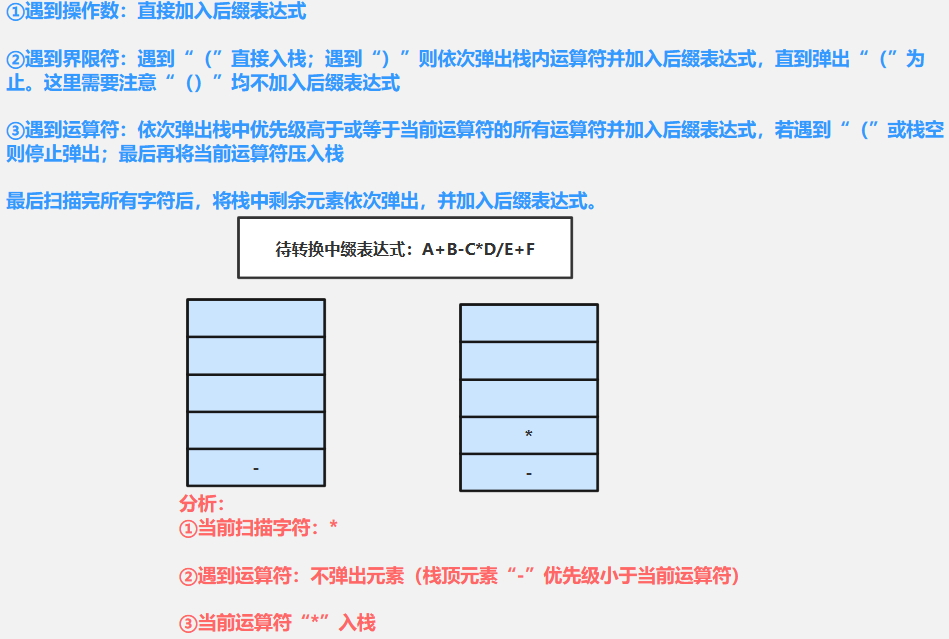
⑦扫描D(操作数):直接加入后缀表达式AB+CD
⑧扫描/(运算符):需要依次弹出栈中优先级高于或等于当前运算符(/)的所有运算符加入后缀表达式,若遇到“(”或栈空则停止弹出-----当前栈顶元素*优先级等于当前运算符(*),弹出*加入后缀表达式:AB+CD*;然后栈中-优先级小于/不再弹出;最后当前运算符(/)入栈
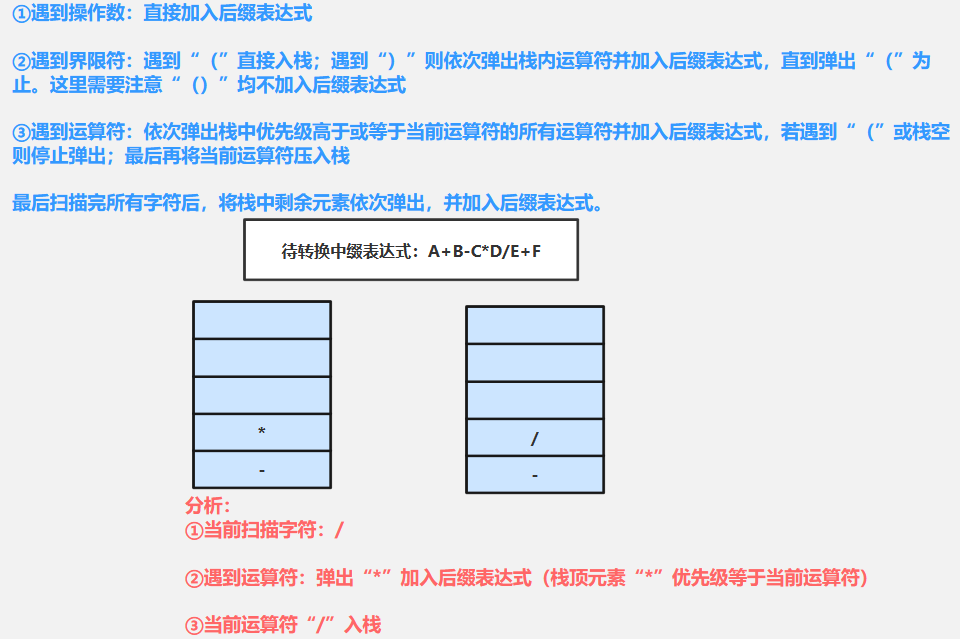
⑨扫描E(操作数):直接加入后缀表达式AB+CD*E
⑩扫描+(运算符):需要依次弹出栈中优先级高于或等于当前运算符(/)的所有运算符加入后缀表达式,若遇到“(”或栈空则停止弹出------当前栈顶元素(-)等于当前运算符(+),弹出(-)加入后缀表达式:AB+CD*E/-;最后当前运算符(+)入栈

⑪扫描F(操作数):直接加入后缀表达式AB+CD*E/-F
⑫扫描完所有字符后,将栈中剩余元素依次弹出,并加入后缀表达式:AB+CD*E/-F+

2、有界限符转换
例子:A+B*(C-D)-E/F----带界限符的中缀表达式转后缀表达式的计算…………还是上述思想,继续操练
从左向右依次扫描
①扫描A(操作数)直接加入后缀表达式:A
②扫描+(运算符):需要依次弹出栈中优先级高于或等于当前运算符(+)的所有运算符加入后缀表达式,若遇到“(”或栈空则停止弹出-------由于栈空则直接退出,最后当前运算符(+)入栈
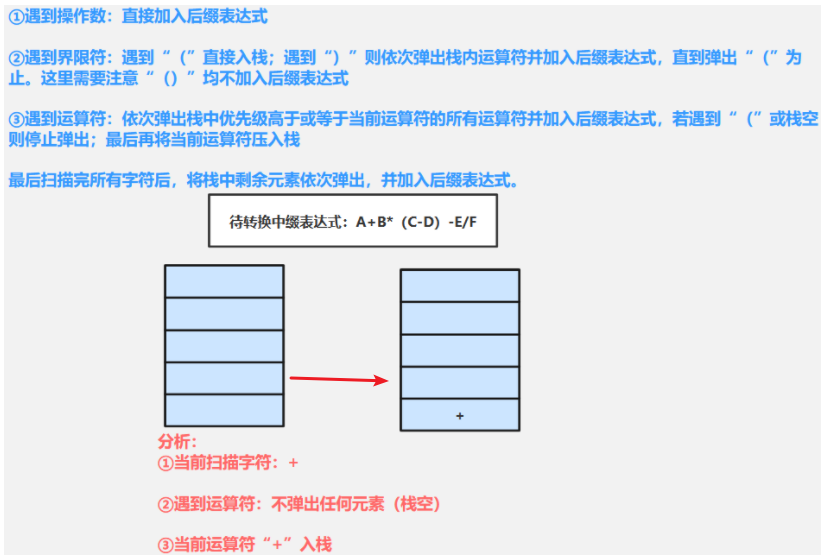
③扫描B(操作数)直接加入后缀表达式:AB
④扫描*(运算符):需要依次弹出栈中优先级高于或等于当前运算符(*)的所有运算符加入后缀表达式,若遇到“(”或栈空则停止弹出-------由于栈顶元素“+”优先级小于当前运算符“*”,不弹出任何元素,最后当前运算符(*)入栈
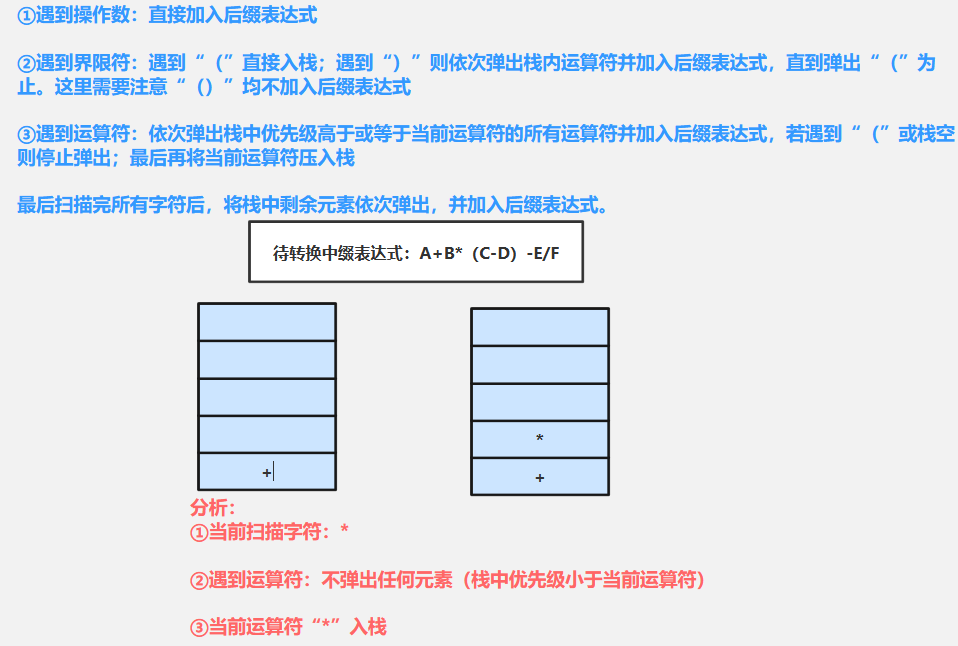
⑤扫描((界限符):遇到“(”直接入栈;遇到“)”则依次弹出栈内运算符并加入后缀表达式,直到弹出“(”为止。-----当前字符“(”直接入栈
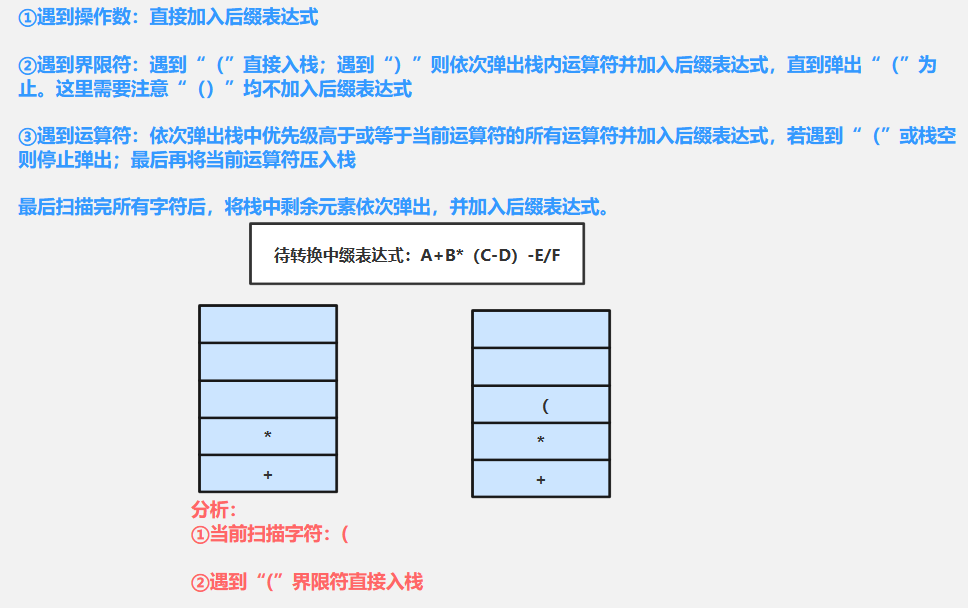
⑥扫描C(操作数)直接加入后缀表达式:ABC
⑦扫描-(运算符):需要依次弹出栈中优先级高于或等于当前运算符(-)的所有运算符加入后缀表达式,若遇到“(”或栈空则停止弹出-----由于栈顶元素是"("停止弹出,当前运算符"+"入栈

⑧扫描D(操作数):直接加入后缀表达式:ABCD
⑨扫描)(界限符):遇到“(”直接入栈;遇到“)”则依次弹出栈内运算符并加入后缀表达式,直到弹出“(”为止。-----依次弹出“-”加入后缀表达式:ABCD-

⑩扫描-(运算符):需要依次弹出栈中优先级高于或等于当前运算符(-)的所有运算符加入后缀表达式,若遇到“(”或栈空则停止弹出------由于栈顶元素“*”优先级高于当前运算符“-”,弹出“*”加入后缀表达式;此时栈顶元素“+”优先级等于当前运算符“-”,弹出“+”加入后缀表达式:ABCD-*+,最后当前运算符“-”入栈
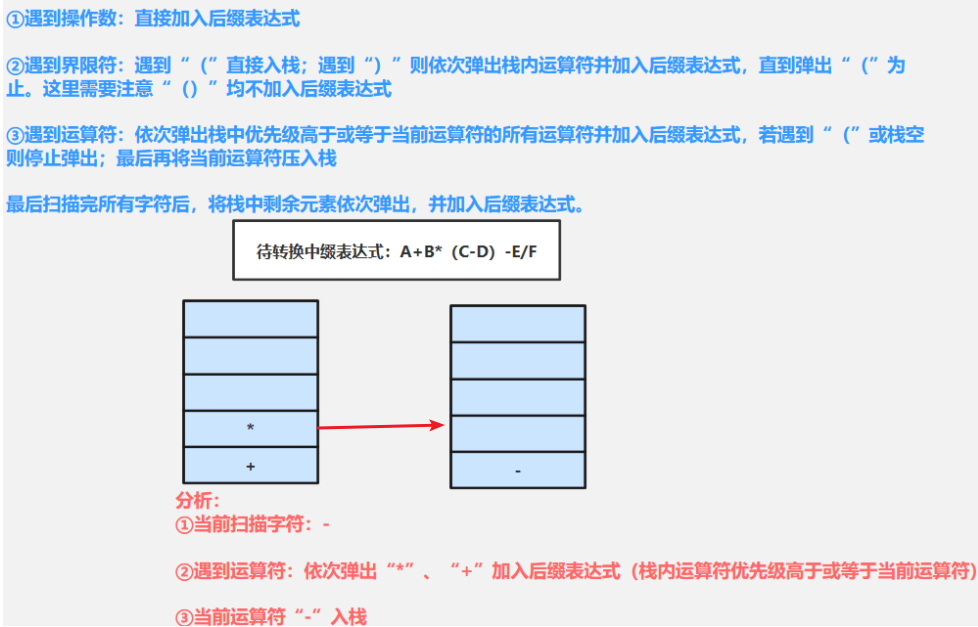
⑪扫描E(操作数):直接加入后缀表达式:ABCD-*+E
⑫扫描/(运算符):需要依次弹出栈中优先级高于或等于当前运算符(/)的所有运算符加入后缀表达式,若遇到“(”或栈空则停止弹出-----由于栈顶元素“-”优先级小于当前运算符,不弹栈顶元素。最后将当前运算符“/”入栈
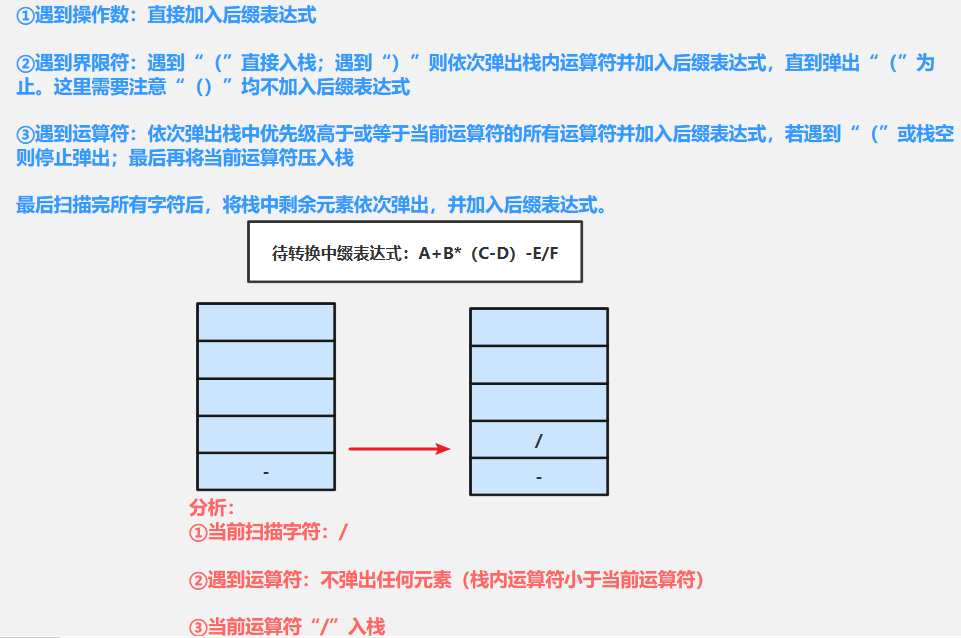
⑬扫描F(操作数):直接加入后缀表达式:ABCD-*+EF
⑭扫描完所有元素后,依次弹出栈内剩余元素,加入后缀表达式得:ABCD-*+EF/-
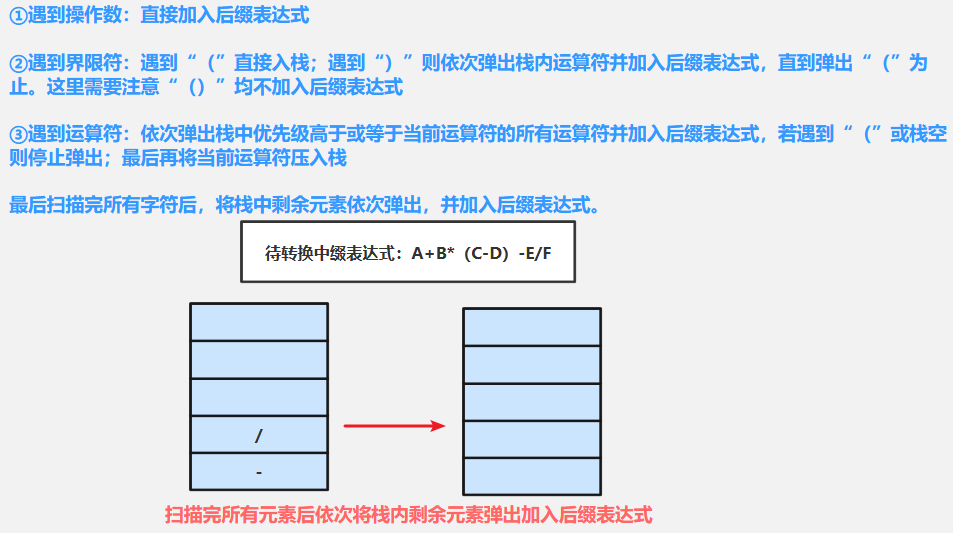
六、终极版--中缀表达式的计算(机算)
以上实现了中缀表达式转后缀表达式的机算方式、后缀表达式的机算,下面就是将以上两个这合并-------中缀表达式的机算
思想:
(1)初始化两个栈,操作数栈和运算符栈
(2)若扫描到操作数,压入操作数栈
(3)若扫描到运算符或界限符,则按照“中缀转后缀”思想压入运算符栈(期间会弹出运算符,每当弹出一个运算符时,就需要弹出两个操作数栈的栈顶元素并执行响应运算,运算结果再压回操作数栈)
(4)最终运算结果就是操作数栈中的唯一一个元素
最终代码实现:


import java.math.BigDecimal; import java.util.*; import java.util.regex.Pattern; /** * @ClassName: StackDemo1 * @Description: * @Author: xiedong * @Date: 2020/9/16 11:51 */ public class StackDemo2 { public static final String regexNumber = "^-?\d+(\.\d+)?$";//数字正则 private static Map<String, Integer> orderMap = new HashMap(); private static final Integer errorNum = Integer.MAX_VALUE; static { orderMap.put("+", 0); orderMap.put("-", 0); orderMap.put("*", 1); orderMap.put("/", 1); orderMap.put("(", 2); orderMap.put(")", 3); } public static void main(String[] args) { //处理数据源 String source = "((15/(7-(1+1)))*3)-(2+(1+1))"; //逆波兰表达式 StringBuilder suffixExpression = new StringBuilder(); //操作数栈 Stack<String> operationStack = new Stack<>(); //运算符栈 Stack<String> arithmeticStack = new Stack<>(); //处理源 getOpLists(source).stream().forEach(per -> { //获取扫描对应优先级 Integer val = orderMap.getOrDefault(per, errorNum); if (Pattern.compile(regexNumber).matcher(per).matches()) { //如果是操作数则直接压入操作数栈 operationStack.push(per); //直接加入后缀表达式 suffixExpression.append(per); } else if (val <= 1) { //如果是运算符:+-*/ if (arithmeticStack.isEmpty()) //栈空则直接入栈 arithmeticStack.push(per); else { //查看当前栈顶元素的优先级 int peekNum = orderMap.get(arithmeticStack.peek()); //当栈顶运算符优先级高于或等于当前运算符的优先级且栈顶元素不为左括号( while (peekNum >= orderMap.get(per) && peekNum <= 1) { //依次弹出栈顶元素--即运算符 String pop = arithmeticStack.pop(); //弹出操作数栈栈顶元素---对应右操作数 String rightOperNum = operationStack.pop(); //弹出操作数栈栈顶元素---对应右操作数 String leftOperNum = operationStack.pop(); //加入后缀表达式(逆波兰表达式) suffixExpression.append(pop); //左右操作数执行对应运算 String tmpResult = doCalculate(pop, leftOperNum, rightOperNum); //运算结果压回操作数栈 operationStack.push(tmpResult); //查看当前栈顶元素的优先级 peekNum = orderMap.get(arithmeticStack.peek()); } //最后当前运算符压入运算符栈 arithmeticStack.push(per); } } else if (val == 2) //左括号直接压入运算符栈 arithmeticStack.push(per); else if (val == 3) {//右括号 String pop = arithmeticStack.pop(); Integer popMapNum = orderMap.get(pop); //遇到右括号则依次弹出运算符栈元素,直到弹出左括号"("为止 while (popMapNum != 2) { //每次弹出一个 运算符,就必须弹出两个操作数执行对应运算,并将结果压回操作数栈中 String rightOperNum = operationStack.pop(); String leftOperNum = operationStack.pop(); //弹出的运算符加入逆波兰表达式 suffixExpression.append(pop); //左右操作数执行对应运算 String tmpResult = doCalculate(pop, leftOperNum, rightOperNum); //运算结果压回操作数栈 operationStack.push(tmpResult); //再次弹出运算符栈---查看是否为左括号"(" pop = arithmeticStack.pop(); popMapNum = orderMap.get(pop); } } } ); //当扫描完所有字符后,依次弹出运算符栈元素,期间每弹出一个运算符,就需要弹出两个操作数进行相应运算,并将结果压回操作数栈 while (!arithmeticStack.isEmpty()) { //依次弹出运算符栈元素 String pop = arithmeticStack.pop(); //加入逆波兰表达式 suffixExpression.append(pop); //期间每弹出一个运算符,就需要弹出两个操作数进行相应运算 String rightNum = operationStack.pop(); String leftNum = operationStack.pop(); String tmpResult = doCalculate(pop, leftNum, rightNum); //运算结果压回操作数栈中 operationStack.push(tmpResult); } System.out.println("结果是:" + operationStack.peek()); System.out.println("逆波兰表达式:" + suffixExpression.toString()); } /** * 分割源字符串 * * @param source 源字符串 * @return */ private static List<String> getOpLists(String source) { ArrayList<String> res = new ArrayList<>(); char[] charArray = source.toCharArray(); StringBuilder sb = new StringBuilder(); for (int i = 0; i < charArray.length; i++) { sb.append(charArray[i]); if (Character.isDigit(charArray[i]) && i != charArray.length - 1 && Character.isDigit(charArray[i + 1])) { continue; } else { res.add(sb.toString()); sb.delete(0, sb.length()); } } return res; } /** * 按对应运算符执行运算 * * @param pop 运算符 * @param leftOperNum 左操作数 * @param rightOperNum 右操作数 * @return */ private static String doCalculate(String pop, String leftOperNum, String rightOperNum) { BigDecimal res = BigDecimal.ZERO; switch (pop) { case "+": res = new BigDecimal(leftOperNum).add(new BigDecimal(rightOperNum)); break; case "-": res = new BigDecimal(leftOperNum).subtract(new BigDecimal(rightOperNum)); break; case "*": res = new BigDecimal(leftOperNum).multiply(new BigDecimal(rightOperNum)); break; case "/": res = new BigDecimal(leftOperNum).divide(new BigDecimal(rightOperNum)); break; } return res.toString(); } }
