手写一个LRU缓存机制

　　前言：不断学习就是程序员的宿命

此题对应力扣题目地址：https://leetcode-cn.com/problems/lru-cache/

　　

一、LRU介绍

　　　LRU是Least Recently Used的缩写，即最近最少使用，是一种常用的页面置换算法，选择最近最久未使用的数据予以淘汰。

二、设计思想

　　1、所谓缓存，必须要有读+写操作，按照命中率的思路考虑，写操作+读操作时间复杂度都需要为O（1）

　　2、特性要求

　　　　a.必须要有顺序之分，区分最近使用的和很久没有使用的数据排序

　　　　b.读和写操作一次搞定

　　　　c.如果容量满了要删除最不常用的数据，每次新访问的还要把新的数据插入到队头

综上所述：查找快、插入快、删除快、且还要先后排序----？什么样的数据结构可以满足这个问题呢？且时间复杂度为O（1）完成操作，你觉得什么样的数据结构合适呢？

答案：LRU的算法核心就是哈希链表（哈希可以保证时间复杂度为O（1）、链表可以保证插入和删除快）

本质就是：HashMap+DoubleLinkedList，时间复杂度是O（1），哈希表+双向链表的结合体

三、LRU实操

1、封装双向链表节点Node作为数据载体

　　可参考JDK源码：AQS抽象队列同步器内部Node（封装Thread等信息）、HashMap内部节点Node　　

   class Node<K, V> {
        K key;
        V value;
        Node<K, V> prev;
        Node<K, V> next;

        public Node() {
            this.prev = this.next = null;
        }

        public Node(K key, V value) {
            this.key = key;
            this.value = value;
            this.prev = this.next = null;
        }
    }

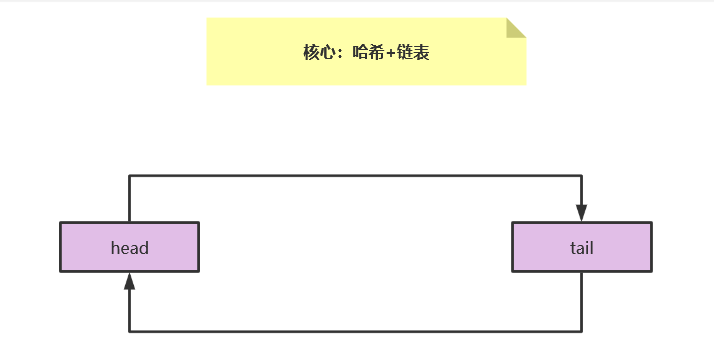
2、双向链表构造方法

    class DoubleLinkedList<K, V> {
        Node<K, V> head;//头节点
        Node<K, V> tail;//尾节点

        public DoubleLinkedList() {
            //头尾哨兵节点
            this.head = new Node<K, V>();
            this.tail = new Node<K, V>();
            this.head.next = this.tail;
            this.tail.prev = this.head;
        }
    }

　　执行完成构造方法以后此时双向链表结构如下：

 3、双向链表添加节点方法

class DoubleLinkedList<K, V> {
        Node<K, V> head;//头节点
        Node<K, V> tail;//尾节点

        public DoubleLinkedList() {
            //头尾哨兵节点
            this.head = new Node<K, V>();
            this.tail = new Node<K, V>();
            this.head.next = this.tail;
            this.tail.prev = this.head;
        }

        /**
         * 添加节点
         */
        public void add(Node<K, V> node) {
            node.next = head.next;
            node.prev = head;
            head.next.prev = node;
            head.next = node;
        }
    }

　　执行添加节点操作如下：

　　

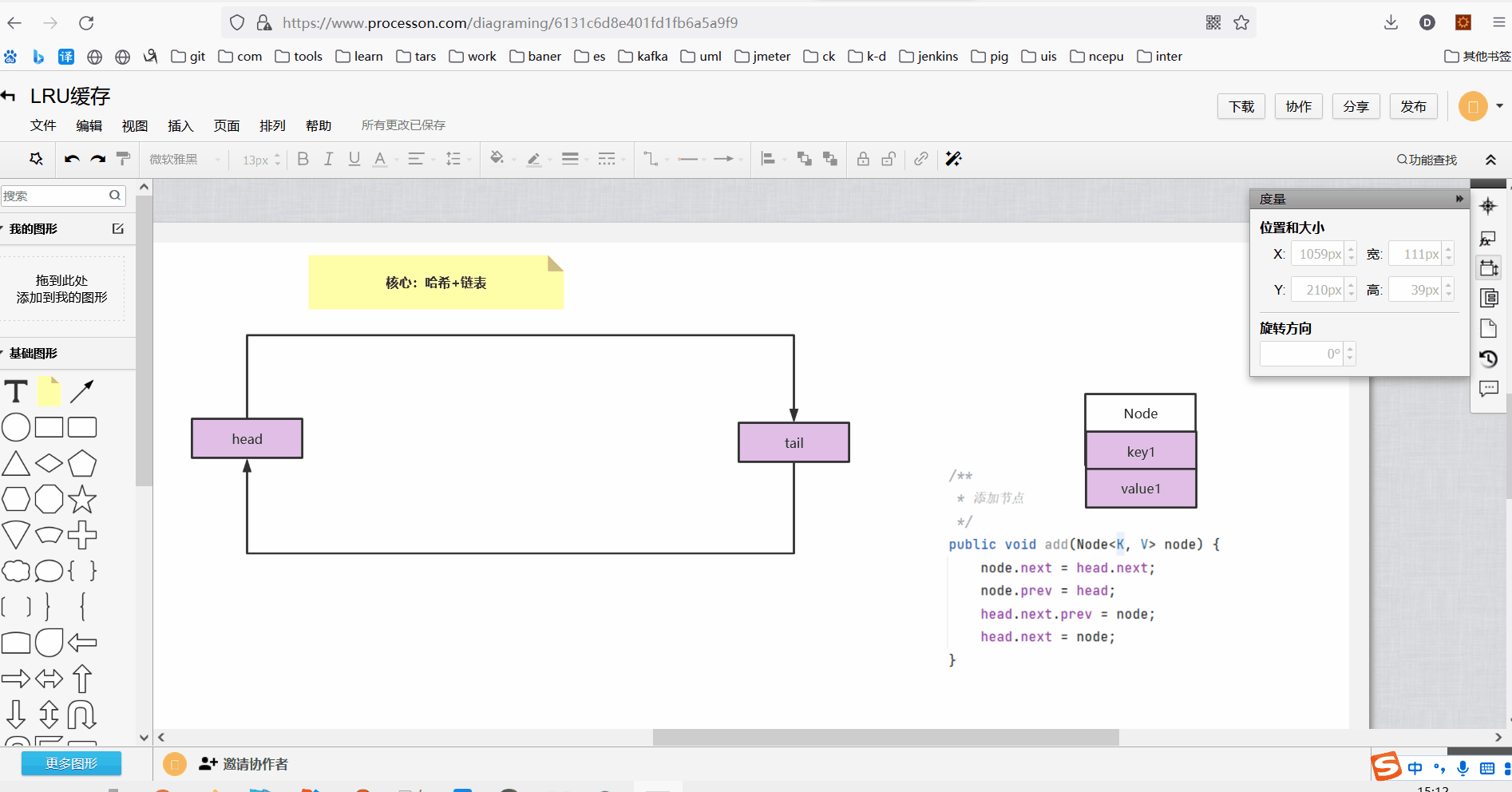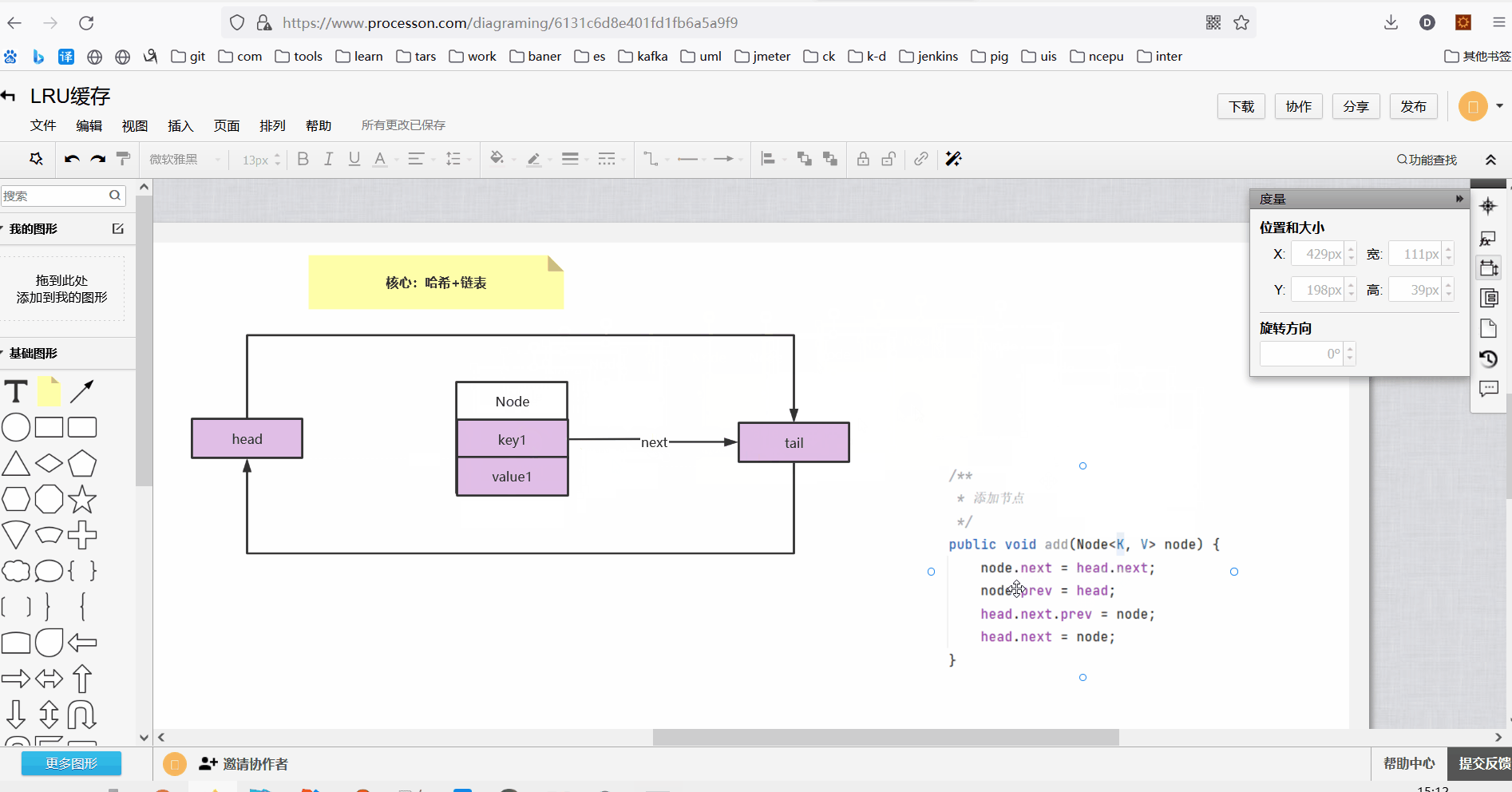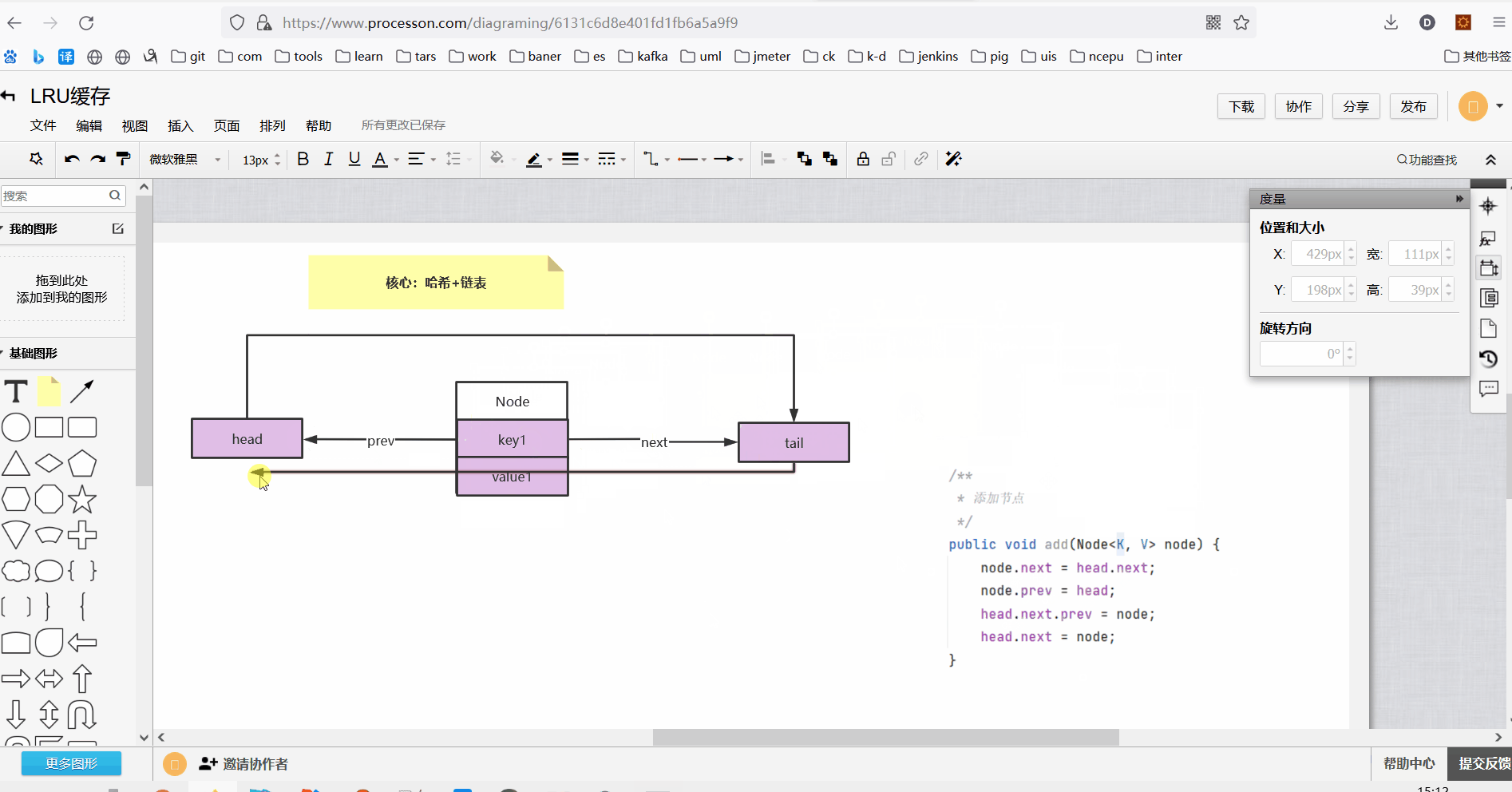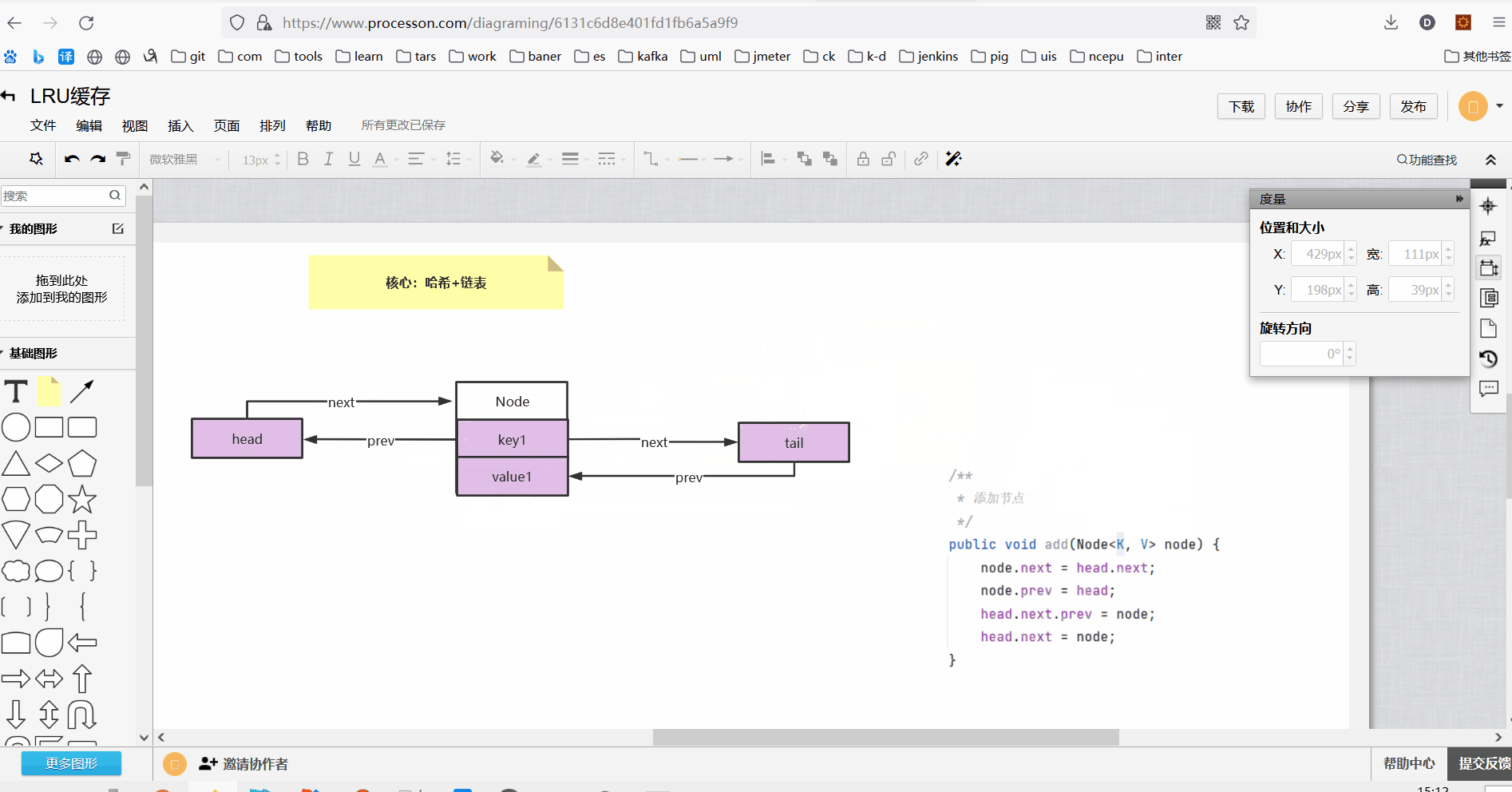
　　执行完添加方法以后此时双向链表结构如下：

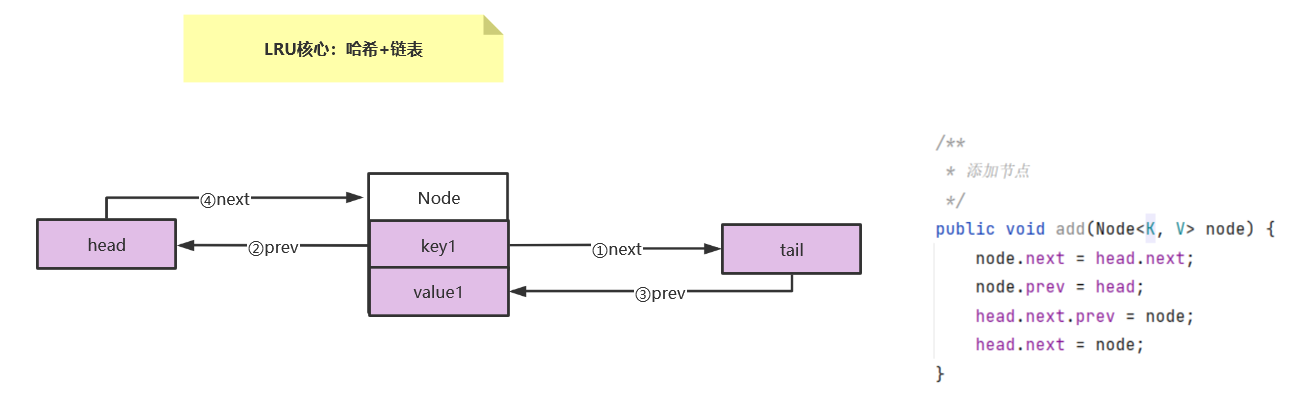
 4、双向链表删除节点

    /**
         * 删除节点
         */
        public void remove(Node<K, V> node) {
            node.next.prev = node.prev;
            node.prev.next = node.next;
            node.prev = null;
            node.next = null;
        }

删除节点操作如下：

5、获取最后一个结点

 /**
         * 获取最后一个节点
         * 将来用作最久不使用的数据
         * @return
         */
        public Node<K, V> getLast() {
            return this.tail.prev;
        }

6、完整代码

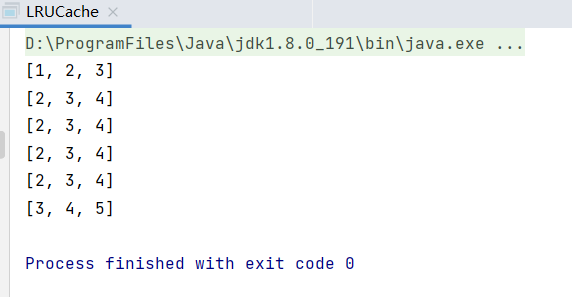
public class LRUCache {
    //容量
    private int capacity;
    //map用于查找 时间复杂度O(1)
    private Map<Integer, Node<Integer, Integer>> map;
    //双向链表
    private DoubleLinkedList<Integer, Integer> doubleLinkedList;
    //构造
    public LRUCache(int capacity) {
        this.capacity = capacity;
        this.map = new HashMap<>();
        this.doubleLinkedList = new DoubleLinkedList<>();
    }

    public Integer get(int key) {
        if (map.containsKey(key)) {
            //查找对应元素 时间复杂度O(1)
            Node<Integer, Integer> node = map.get(key);
            //使用一次就删除
            this.doubleLinkedList.remove(node);
            //重新放在头结点位置（认为是最近使用的）
            this.doubleLinkedList.add(node);
            return node.value;
        }
        return -1;
    }

    public void put(int key, int value) {
        if (map.containsKey(key)) {
            //如果存在则进行更新
            Node<Integer, Integer> node = map.get(key);
            node.value = value;
            map.put(key, node);
            //更新完成以后放至头结点位置，认为是最近使用的
            this.doubleLinkedList.remove(node);
            this.doubleLinkedList.add(node);
        } else {
            //如果不存在则进行判断容量是否达上限
            if (map.size() == this.capacity) {
                //最后一个节点即最近最少使用的
                Node<Integer, Integer> lastNode = this.doubleLinkedList.getLast();
                map.remove(lastNode.key);
                //删除最近最少使用的
                doubleLinkedList.remove(lastNode);
            }
            Node<Integer, Integer> node = new Node<>();
            node.key = key;
            node.value = value;
            map.put(key, node);
            //添加至头结点位置，认为是最近刚刚使用的
            this.doubleLinkedList.add(node);
        }

    }

    //map负责查找，构建一个虚拟的双向链表，里面为一个个Node，作为数据载体
    //双向链表节点
    class Node<K, V> {
        K key;
        V value;
        Node<K, V> prev;
        Node<K, V> next;

        public Node() {
            this.prev = this.next = null;
        }

        public Node(K key, V value) {
            this.key = key;
            this.value = value;
            this.prev = this.next = null;
        }
    }

    class DoubleLinkedList<K, V> {
        Node<K, V> head;//头节点
        Node<K, V> tail;//尾节点

        public DoubleLinkedList() {
            //头尾哨兵节点
            this.head = new Node<K, V>();
            this.tail = new Node<K, V>();
            this.head.next = this.tail;
            this.tail.prev = this.head;
        }

        /**
         * 添加节点
         */
        public void add(Node<K, V> node) {
            node.next = head.next;
            node.prev = head;
            head.next.prev = node;
            head.next = node;
        }

        /**
         * 删除节点
         */
        public void remove(Node<K, V> node) {
            node.next.prev = node.prev;
            node.prev.next = node.next;
            node.prev = null;
            node.next = null;
        }

        /**
         * 获取最后一个节点
         * 将来用作最久不使用的数据
         *
         * @return
         */
        public Node<K, V> getLast() {
            return this.tail.prev;
        }
    }

    public static void main(String[] args) {
        LRUCache lruCache = new LRUCache(3);
        lruCache.put(1,1);
        lruCache.put(2,2);
        lruCache.put(3,3);
        System.out.println(lruCache.map.keySet());
        lruCache.put(4,4);
        System.out.println(lruCache.map.keySet());

        lruCache.put(3,1);
        System.out.println(lruCache.map.keySet());
        lruCache.put(3,1);
        System.out.println(lruCache.map.keySet());
        lruCache.put(3,1);
        System.out.println(lruCache.map.keySet());
        lruCache.put(5,1);
        System.out.println(lruCache.map.keySet());
    }
}

验证结果如下：