有n (n>=3)个硬币，其中一个是假币，已知假币的重量比其他的要重一些，你有一架天平。现在要称出那个是假币来。
解析：
首先我们先来考虑最简单的问题1.为了方便叙述，把n个硬币按1,2...，n顺次编号。
若n=3，把一号硬币放在天平左边，二号币放在天平右边。如果天平:
1.左偏，一号重，是假币。
2.右偏，二号重，是假币。
3.保持平衡，那么一二都是正常的硬币，因此只有可能三号是假币了。
因此n=3，至多一次就能称出哪个是假币，记作f(3)=1.
下面考虑n=9.把所有硬币分成三组，a{1.2.3} B{4.5.6} C{7.8.9}。A组的硬币放在左边，B组放在右边。如果天平：
1.左偏，则假币在A里面。
2.右偏，则假币在B组里面。
3.保持平衡，在C组。
无论在哪个组里面，我们已经把假币的范围从9缩小到3，也就是减少到了原来的1/3.之前我们研究过，3个硬币1次就能称出来，故而f(9)=2.
不难推广到一般情况：
定理1.1 f(3n)=n
证明：n=1,2时，已证。设n=k成立，则f(3k)=k;下面考虑n=k+1的情况。
将3k+1个硬币分成三堆，使得|A|=|B|=|C|=3k。把A放在天平左边，B放在右边。
天平：
1、左偏，假币在A
2、右偏，假币在B
3、平衡，假币在C
无论哪种结果，我们都把假币的范围缩小到了3k个硬币里面。而f(3k)=k，故而f(3k+1)=k+1。
综上，定理1.1成立。
稍经分析不难得到：
定理1.2 f(n)=(log3n) 向上取整
这个证明和定理1.1完全类似，分n mod 3 = 0, 1, 2适当讨论即可。
我们必须注意到(log3n) 向上取整是可行的，应为我们能构造出这样一个方案。问题是它是不是最优的？
我们采取的方案是每次将硬币尽量均匀的分成三份，这样做的根据就是天平只有三种结果：左偏，右偏，平衡。于是就能保证无论假币在哪一份都能将结果的范围缩小到原来的1/3.从感性上认识，这应该是最优的了。
为了更加严格的证明最优性，我们引进判定树的概念。
下图就是n=9时的一种判定树：
1、叶子节点代表一种可能的结果。
2、非叶子节点代表一次称量。
3、非叶子节点至多有三个儿子，分别代表天平的左偏、右偏、平衡三种情况。
任意一种称量方案都能唯一的表示成一棵判定树；反过来一棵判定树也唯一对应一种称量方案。
容易看出判定树的深度就是称量次数。这就是我们之所以引进它的原因。
做出判断之前，谁也无法预知哪个硬币是假币，每个都有可能是我们的目标；因此一个有意义的判定树应该具有至少n个叶子节点。
n个叶子节点的树的深度h ≥ log3上取证，故而可以证明，f(n)=log3 上取整是最优的。
我们的结论是：有n（n≥3次，就能找出那个假币。）个硬币，其中一个是假币，假币的重量比其他的要重一些。给一架天平，至少称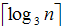
次，就能找出那个假币。
具体的方案是将硬币每次都尽量均匀的三分。
让我们总结一下。
“三分”是整个解法的核心。我们选择三分，而不是二分或者四分是有原因的，它的本质是由判定树的特殊结构——三叉树——所决定的。
同时还必须注意一点，我们在三分的时候有两个字很讲究：“均匀”。实际上h ≥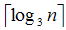
中的‘=’当且仅当硬币被均匀地分配时才能到达。
这里说的“均匀”是指“在最坏情况下获得最好的效果”。因为一棵树的深度是由它根节点儿子中深度最大的儿子决定的，为了使得整个树深度最小，我们就要务必使得深度最大的儿子深度最小，这就是“均匀”分配的理论根据。
练习：第 12 届全国青少年信息学奥林匹克联赛初赛题 现有 80枚硬币，其中有一枚是假币，其重量稍重，所有真币的重量都相同，如果使 用不带砝码的天平称重，最少需要称几次，就可以找出假币？你还要指出第1次的称重方法。请写出你的结果：
答案：4次 ；第一步，分成三组：27，27，26，将前2组放到天平上。