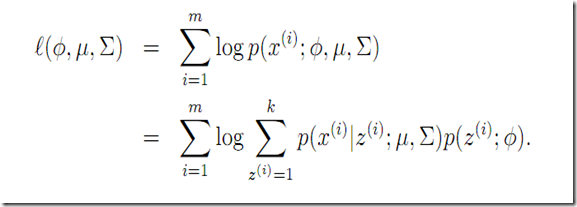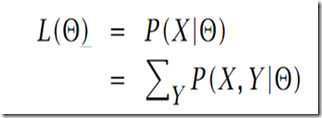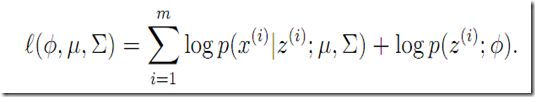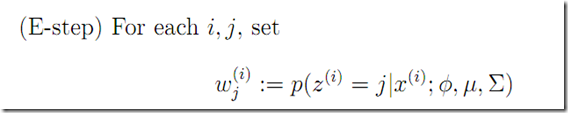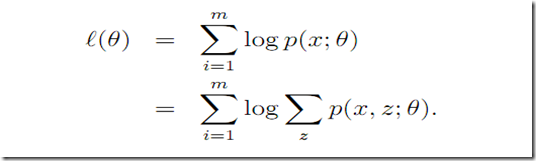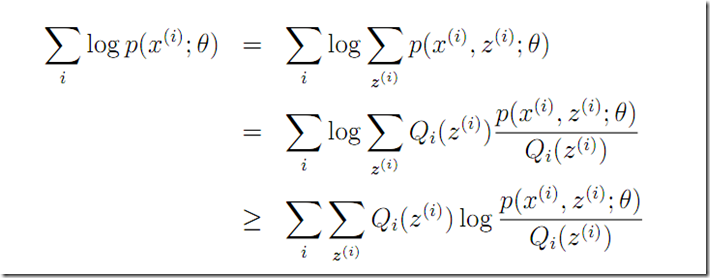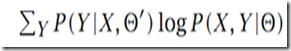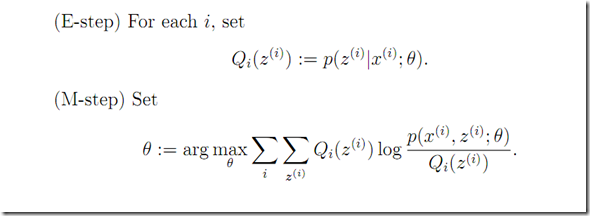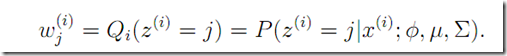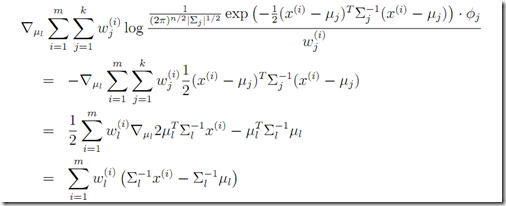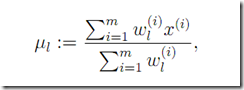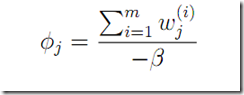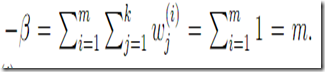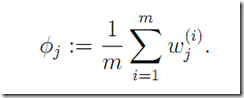Andrew Ng 关于EM有两个不错的课件
http://www.stanford.edu/class/cs229/notes/cs229-notes7b.pdf Mixtures of Gaussians and the EM algorithm
http://www.stanford.edu/class/cs229/notes/cs229-notes8.pdf The EM algorithm
关于课件1,EM感性认识-高斯混合分布
和我在1中翻译的ZHAI的文章中用到mixture model不同,作者的例子是mixture of gaussians。
数据点是由一系列高斯分布的混合。
要最大话的似然函数可以表示为
直接MLE计算的困难仍然是log(a+b+c..) + log(a2+b2+c2…) log里面的+是个大麻烦。
如果我们知道具体![]() 是啥,即知道了具体是这个k个高斯分布中哪一生成了
是啥,即知道了具体是这个k个高斯分布中哪一生成了![]() ,则有
,则有
和1中一样的log(a+b)木有了,。。。 有的是log(a) + log(b)
这个情况下再估算参数很简单
现在问题是![]() 未知,hidden.. unknown, 那EM之
未知,hidden.. unknown, 那EM之
E step估算hidden variable 的后验概率。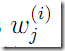 可看做是
可看做是![]() 的soft guess!
的soft guess!
与KMEANS相比,KMEANSE是hard cluster assignment c(i),而这里是是soft assignment 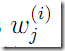
关于课件2,EM理性认识
凸函数的性质
另外重要的是何时=成立呢,constant!----------------------
EM算法推导
这里的思路和1中有什么不同?
难于计算,核心是hidden变量![]() 如果被观察到则计算就变的容易。
如果被观察到则计算就变的容易。
OK下面也是尝试推导下界,和总结1中证明的推导思路不同而已。
Q(i)定义很关键定义为z(i)的分布
f(e(x)) >= e(f(x)) log 是concave 函数,另外其它地方是否类似也有用到凹凸函数这个不等式性质的呢,考虑总结1中提到的KL(p||q)>=0 KL(p||q) 定义参考前面的总结《PRML学习笔记-信息论》也是一样的形式p(x)log(q(x)/p(x))求和或者积分
这个推导很牛,因为这样log(a+b…)即log里面的+就木有了!
这里对于任意的z(i)的分布Q(i)我们都给出了一个下界,那么如何选择Q(i)分布?
如果我们现在有对于参数![]() 的猜测,我们很自然的希望取得the lower-bound tight at that value of
的猜测,我们很自然的希望取得the lower-bound tight at that value of ![]() ,
,
we’ll make the inequality above hold with equality at our particular ![]() (取==了!),后面我们将会看到这将帮助我们证明EM算法的单调递增性)。
(取==了!),后面我们将会看到这将帮助我们证明EM算法的单调递增性)。
如果我们要取=那么需要constant!
NG课件始终用这个Qfunction 和前面的略有不同但是个人认为是相同的,因 Q = q * log (a/q) = q * log (a) – q* log(q)后面没有参数![]() 可略去(因为当前步骤M前已经确定了它。。要估计的
可略去(因为当前步骤M前已经确定了它。。要估计的![]() 只存在于分子p(..),
只存在于分子p(..),
下面NG给的mixture gaussian 例子也证明了这样)。
算法为什么收敛
再看高斯混合模型
E step is easy
M step
注意这里的![]() ,想想前面总结1中的
,想想前面总结1中的![]() 是不是一样呢,只是那里是固定好了已经假定。另外注意
是不是一样呢,只是那里是固定好了已经假定。另外注意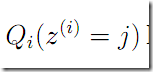 和
和 的区别。
的区别。
下面还是求偏导数为0即可。
综上,感觉NG的课件比总结1更深入更透彻:)总结1可以看成一个特例简单化了的情形。NG的证明也感觉更加优美,紧凑。