实现主成分分析与白化

在这一节里，我们将总结PCA,ZCA白化算法，并描述如何使用高效的线性代数库来实现它们。

首先，我们需要确保数据的均值（近似）为零。对于自然图像，我们通过减去每个图像块(patch)的均值（近似地）来达到这一目标。为此，我们计算每个图像块的均值，并从每个图像块中减去它的均值。Matlab实现如下：

avg = mean(x, 1);     % 分别为每个图像块计算像素强度的均值。 
x = x - repmat(avg, size(x, 1), 1);

下面，我们要计算 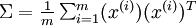 ，如果你在Matlab中实现（或者在C++, Java等中实现，但可以使用高效的线性代数库），直接求和效率很低。不过，我们可以这样一气呵成。

sigma = x * x' / size(x, 2);

这里，我们假设x为一个数据结构，其中每列表示一个训练样本（所以x是一个n×m的矩阵）。

接下来，PCA计算Σ 的特征向量。你可以使用Matlab的 eig函数来计算。但是由于 Σ 是对称半正定的矩阵，用 svd 函数在数值计算上更加稳定

 具体来说，如果你使用

[U,S,V] = svd(sigma);

那矩阵 U 将包含 Sigma 的特征向量（一个特征向量一列，从主向量开始排序），矩阵S 对角线上的元素将包含对应的特征值（同样降序排列）。矩阵 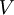 等于 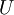 的转置，可以忽略。

 （注意svd函数实际上计算的是一个矩阵的奇异值和奇异向量，就对称半正定矩阵的特殊情况来说，它们对应于特征值和特征向量，这里我们也只关心这一特例。）

 最后，我们可以这样计算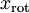 和  ：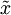

xRot = U' * x;          % 数据旋转后的结果。 

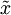= U(:,1:k)' * x; % 数据降维后的结果，这里k希望保留的特征向量的数目。

这以 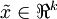 的形式给出了数据的PCA表示。顺便说一下，如果 x 是一个包括所有训练数据的 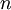× 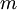矩阵，这也是一种向量化的实现方式，上面的式子可以让你一次对所有的训练样本计算出 x_rot 和  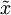。得到的 x_rot 和  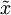中，每列对应一个训练样本。

 为计算PCA白化后的数据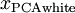 ，可以用

xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;

因为s的对角线包括了特征值 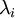 ，这其实就是同时为所有计算样本i计算 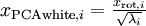的简洁表达。

最后，你也可以这样计算ZCA白化后的数据: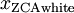

xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;