zoukankan html css js c++ java

KMeans聚类算法

简介

聚类是一种无监督的机器学习任务，它可以自动将数据划分成类cluster。
- 聚类
  - 给事物打标签，寻找同一组内的个体之间的一些潜在的相似模式。力图找到数据的自然分组kmeans
因此聚类分组不需要提前被告知所划分的组应该是什么样的。
因为我们甚至可能都不知道我们在寻找什么，所以聚类是用于知识发现而不是预测

理解

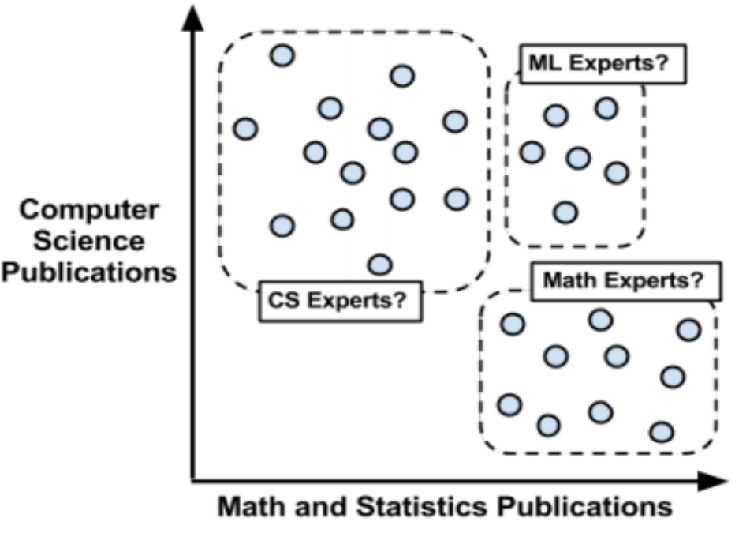
1575091989232

聚类原则是一个组内的记录彼此必须非常相似，而与该组之外的记录截然不同。
所有聚类做的就是遍历所有数据然后找到这些相似性
使用距离来分配和更新类
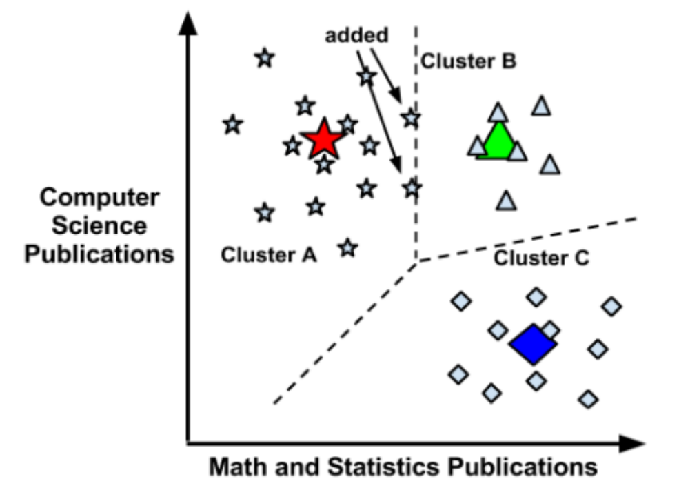
- 由以上一系列图可知, 该区域被划分为三个cluster(簇), 当有新的单位被添加到该区域时, 根据该点到簇中心的距离将该单位进行划分并优化。

距离测度

欧氏距离测度（EuclideanDistanceMeasure）
平方欧氏距离测度（SquaredEuclideanDistanceMeasure）
曼哈顿距离测度（ManhattanDistanceMeasure）

图中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。
- 曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离，即d（i，j）=|x_i-x_j|+|y_i-y_j|。
- 对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此，曼哈顿距离又称为出租车距离
余弦距离测度（CosineDistanceMeasure）
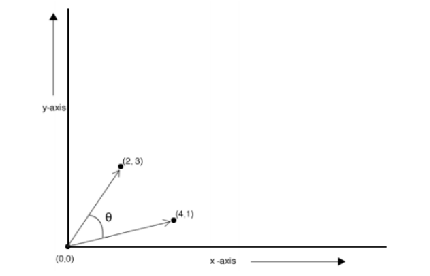
谷本距离测度（TanimotoDistanceMeasure）
- 同时表现夹角和距离的距离测度
加权距离测度（WeightedDistanceMeasure)

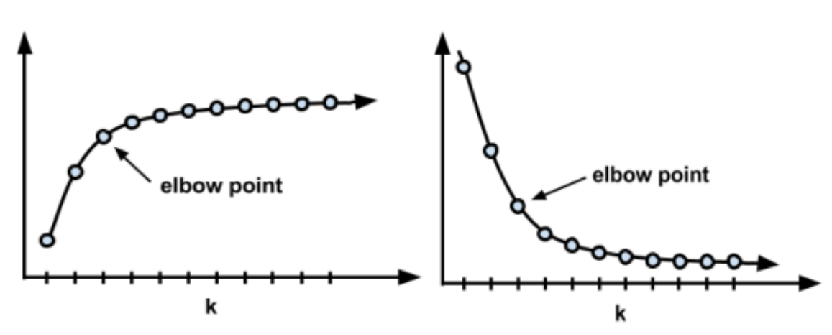
选择适当的聚类数

肘部法

算法思想

以空间中K个点为中心进行聚类，对最靠近他们的对象归类，通过迭代的方法，逐次更新各聚类中心的值，直到得到最好的聚类结果

算法流程总结

适当选择c个类的初始中心
在第K次迭代中，对任意一个样本，求其到c各中心的距离，将该样本归到距离最短的中心所在的类
利用均值等方法更新该类的中心值
对于多有的c个聚类中心，如果利用2,3的迭代法更新后，值保持不变，则迭代结束，否则继续迭代

算法缺陷

聚类中心的个数K 需要事先给定，但在实际中这个 K 值的选定是非常难以估计的。很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适。
Kmeans需要人为地确定初始聚类中心，不同的初始聚类中心可能导致完全不同的聚类结果。（可以使用Kmeans++算法来解决）

Kmeans++算法

从输入的数据点集合中随机选择一个点作为第一个聚类中心
对于数据集中的每一个点x，计算它与最近聚类中心(指已选择的聚类中心)的距离D(x)
选择一个新的数据点作为新的聚类中心，选择的原则是：D(x)较大的点，被选取作为聚类中心的概率较大
重复2和3直到k个聚类中心被选出来
利用这k个初始的聚类中心来运行标准的k-means算法

SparkMrLib案例

在进入案例之前我们先要前置了解一下稀疏向量与稠密向量

稀疏向量: (100,[0,2,5],[1.0,3.0,8.0])
- 表示该向量内有100个数, [0, 2, 5]表示第0,2,5的位置上有数, [1.0,3.0,8.0]为0,2,5位置上所对应的值。
稠密向量: 就是把整个向量全都列出来

Demo:

import org.apache.spark.ml.linalg
import org.apache.spark.ml.linalg.{Vectors}


object VectorTest {


    def main(args: Array[String]): Unit = {

        //稠密向量 DenseVector
//        val denseVector: linalg.Vector = Vectors.dense(1.0, 0.0, 3.0)
        //稀疏向量 SparseVector
        val sparseVector: linalg.Vector = Vectors.sparse(100, Array(0, 2, 5), Array(1.0, 3.0, 8.0))

//        println("稠密向量: " + denseVector)
//
        println("稀疏向量: " + sparseVector)
////
//        println("稠密向量转成稀疏向量： " + denseVector.toSparse)
////
        println("稀疏向量转成稠密向量： " + sparseVector.toDense)



    }
}

案例1

kmeans_data.txt

0.0 0.0 0.0
0.1 0.1 0.1
0.2 0.2 0.2
0.4 0.4 0.4
0.5 0.5 0.5
9.8 0.8 0.8
9.0 9.0 9.0
9.1 9.1 9.1
9.2 9.2 9.2

代码

import org.apache.spark.ml.clustering.{KMeans, KMeansModel}

import org.apache.spark.ml.linalg.{ SQLDataTypes, Vectors}
import org.apache.spark.rdd.RDD
import org.apache.spark.sql.types._
import org.apache.spark.sql._


object KMeans1 {

    def main(args: Array[String]) {

        val spark = SparkSession
            .builder
            .master("local")
            .appName("Kmeans")
            .getOrCreate()

        val data: RDD[String] = spark.sparkContext.textFile("kmeans_data.txt")

        //数据转化...
        val rdd: RDD[Row] = data.map(s => Row(Vectors.dense(s.split(' ').map(_.toDouble))))

        val schema = StructType(List(
            StructField("features", SQLDataTypes.VectorType, nullable = false)
        ))

        val df: DataFrame = spark.createDataFrame(rdd, schema)

        val kmeans = new KMeans()
        //聚类数...
        kmeans.setK(3)
        //最大迭代次数
        kmeans.setMaxIter(20)
        //随机种子...
        kmeans.setSeed(1L)

        val model: KMeansModel = kmeans.fit(df)

        //中心点位置....
        model.clusterCenters.foreach(println)

        //评估模型的好坏，使用平方欧式距离测度
        val errors: Double = model.computeCost(df)

        println("平方误差: " + errors)

        model.save("model/kmeans")

        spark.close()

    }
}

执行结果
```
平方误差: 0.5759999999999452
```

案例2

代码

import java.util

import org.apache.spark.ml.clustering.KMeansModel
import org.apache.spark.ml.linalg.{SQLDataTypes, Vectors}
import org.apache.spark.sql.{DataFrame, Row, SparkSession}
import org.apache.spark.sql.types.{StructField, StructType}

object KMeans2 {

    def main(args: Array[String]) {

        val spark = SparkSession
            .builder
            .master("local")
            .appName("KmeansTest")
            .getOrCreate()
		// 从上一次存储的模型拿
        val model = KMeansModel.load("model/kmeans")

        //中心点位置...
        model.clusterCenters.foreach(println)

        //测试数据...将这些数据进行"分类.."
        val testData: util.List[Row] = util.Arrays.asList(
            Row(Vectors.dense(Array(-0.1, 0.0, 0.0))),
            Row(Vectors.dense(Array(9.0, 9.0, 9.0))),
            Row(Vectors.dense(Array(3.0, 2.0, 1.0)))
        )

        val schema = StructType(List(
            StructField("features", SQLDataTypes.VectorType, nullable = false)
        ))

        val df = spark.createDataFrame(testData,schema)

        val result: DataFrame = model.transform(df)

        result.show()

        spark.close()

    }
}

python算法实现

# -*- coding: utf-8 -*-
#!/usr/bin/env python

from collections import defaultdict
from random import uniform
from math import sqrt

def avg_point(points):
    """
      接收一列点集, 每个点都有相同的维度2， 返回所有点的中心点集
    """
    dimensions = len(points[0])

    new_center = []

    for dimension in range(dimension):
        dim_sum = 0
        for p in points:
            dim_sum += p[dimension]

        # 获取每个维度的平均值m 并将生成的点加入到new_center数组中    
        new_center.append(dim_sum / float(len(points)))

    return new_center

def update_centers(date_set, assignments):
    """
     接收一个数据集以及一列任务, 两个list的参数必须一一对应
     计算每个标记组的中心
     返回中心集
    """
    new_means = defaultdict(list)
    centers = []
    for assignment, point in zip(assignments, date_set):
        new_means[assignment].append(point)

    for points in new_means.values():
        centers.append(point_avg(points))

    return centers   

def distance(a, b):
    """
    两点间距离
    """
    dimensions = len(a)

    _sum = 0
    for dimension in range(dimensions):
        difference_seq = (a[dimension] - b[dimension]) ** 2
        _sum += difference_seq

    return sqrt(_sum)   

def assign_points(data_points, centers):
    """
    传入一个数据集和中间点, 并将传入的点分类给对应的中心点
    """
    assignments = []
    for point in data_points:
        shortest = float('Inf')
        shortest_index = 0
        for i in range(len(centers)):
            val = distance(point, centers[i])
            if val < shortest:
                shortest = val
                shortest_index = if
        assignments.append(shortest_index)        

    return assignments  

def generate_k(data_set, k):
    """
    生成基准值k
    """
    centers = []
    dimensions = len(data_set[0])
    min_max = defaultdict(int)

    for point in data_set:
        for i in range(dimensions):
            val = point[i]
            min_key = 'min_%d' % i
            max_key = 'max_%d' % i
            if min_key not in min_max or val < min_max[min_key]:
                min_max[min_key] = val
            if max_key not in min_max or val > min_max[max_key]:
                min_max[max_key] = val 

    for _k in range(k):
        rand_point = []
        for i in range(dimensions):
            min_val = min_max['min_%d' % i]
            max_val = min_max['max_%d' % i]

            rand_point.append(uniform(min_val, max_val))
        centers.append(rand_point)    
    return centers  


    def k_means(dataset, k):
        k_points = generate_k(dataset, k)
        assignments = assign_points(dataset, k_points)
        old_assignments = None
        times = 0
        while assignments != old_assignments:
            time += 1
            print('times:', times)
            new_centers = update_centers(dataset, assignments)
            old_assignments = assignments
            assignments = assign_points(dataset, new_centers)

        return (assignments, dataset)

查看全文

相关阅读:
第二阶段小组站立会议-4-26
小组站立会议-2014-04-25张永组
 第二阶段小组站立会议-2014-04-24
小组站立会议-张永组-4-23
第二阶段会议-阶段目标-张永组
 小组项目第二阶段会议--2014420
团队下阶段任务分配会议记录-张永组
 Floaty Fish（内测版）发布前一天-------张永组
 电梯调度设计之初感想——蔡迎盈&&曹玉松
 单元测试——我的认识

原文地址：https://www.cnblogs.com/ronnieyuan/p/11963173.html