1, 树,平时最常用的树就是二叉树(其实也有多叉树),二叉树可以用链表和数组来存储。
2,二叉树,最多只有两个子节点,满二叉树是指叶子节点都在最底层,其余所有节点都有左右2个子节点,他是一种特殊的完全二叉树。
3. 完全二叉树,是指叶子节点都在最底2层,最后一层叶子节点靠左边排列,并且除了最后一层,其他节点个数都达到最大。
4. 某棵二叉树是一棵完全二叉树,那用数组存储是最节省内存的一种方式。只会浪费一个下标未0的存储位置。
5. 二叉树的遍历,有前序、中序和后续,实际上他们是一个递归过程,遍历的时间复杂度为O(n)
二叉查找树,Binary Search Tree, BST
又叫二叉搜索树,是为了实现快速查找而生的,定义是在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值,中序遍历出来就是一个升序集合。插入、删除、查找操作时间复杂度才是 O(logn)
它与散列表比较来看,散列表的构造比二叉查找树要复杂,需要考虑的东西很多。比如散列函数的设计、冲突解决办法、扩容、缩容等。平衡二叉查找树只需要考虑平衡性这一个问题,而且这个问题的解决方案比较成熟、固定。
红黑树
是一种平衡二叉查找树,红黑树的插入、删除、查找各种操作性能都比较稳定,不会退化。
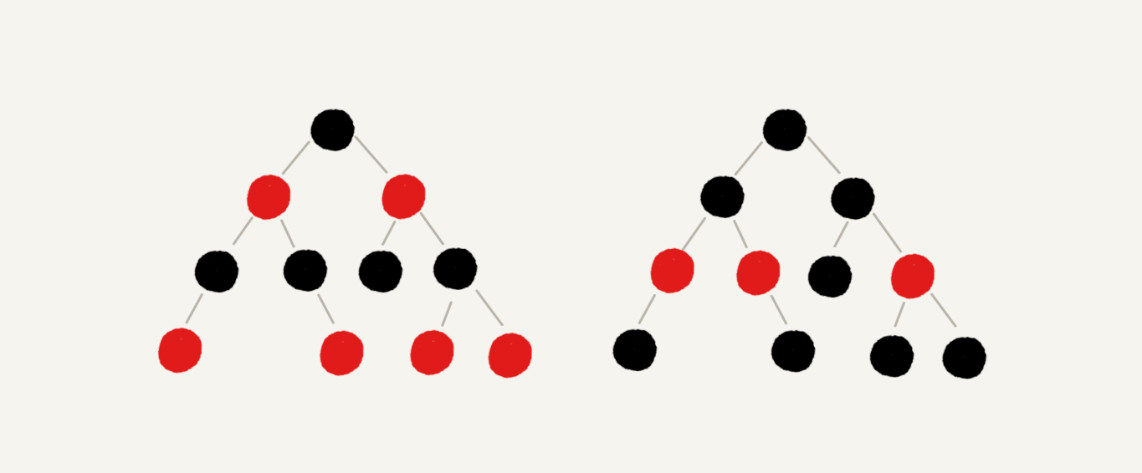
红黑树特点
根节点是黑色的;
每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据;
任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的;
每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;
B树
B+ 只存索引,比如数据库的Index,非聚集索引,不确定的m叉平衡搜索树,索引存在硬盘里,减少IO操作,查询效率更高,单插入、删除时候需要维护。
B树和B-树,其实是同一个东东,他不仅存索引,还存对应的数据,它们其实是B+树的低配版本。
堆,又名优先级队列
堆是一个特殊的完全二叉树
堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值
所以有大顶堆,小顶堆,存储top k大的数,中位数问题,以及衍生的99%接口访问时间等问题
还有堆排序,先构建一个堆,比如小顶堆,然后在依次拿出堆顶元素放到数组的对应位置,就是一个升序结果的数组。
Leetcode原题
a. 翻转二叉树
https://leetcode-cn.com/problems/invert-binary-tree/ 递归
b. 二叉数最大深度
https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/ 递归和BFS
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
} else {
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
return Math.max(leftHeight, rightHeight) + 1;
}
}
}
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root);
int ans = 0;
while (!queue.isEmpty()) {
int size = queue.size();
while (size > 0) {
TreeNode node = queue.poll();
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
size--;
}
ans++;
}
return ans;
}
}
c. 验证是否是一棵有效的二叉查找数
https://leetcode-cn.com/problems/validate-binary-search-tree/
d. 二叉树路径总和