w
https://en.wikipedia.org/wiki/Amortized_analysis
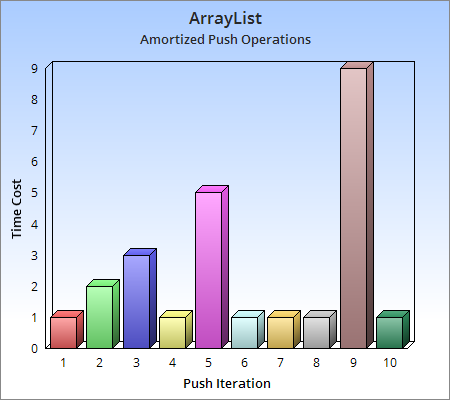
In computer science, amortized analysis is a method for analyzing a given algorithm's time complexity, or how much of a resource, especially time or memory in the context of computer programs, it takes to execute. The motivation for amortized analysis is that looking at the worst-case run time per operation can be too pessimistic.[1]
While certain operations for a given algorithm may have a significant cost in resources, other operations may not be as costly. Amortized analysis considers both the costly and less costly operations together over the whole series of operations of the algorithm. This may include accounting for different types of input, length of the input, and other factors that affect its performance.[2]