（补题）牛客国庆集训派对day4

C、Emergency Evacuation

题意：通过样例也能看懂题.jpg，问所有人都出去的时间

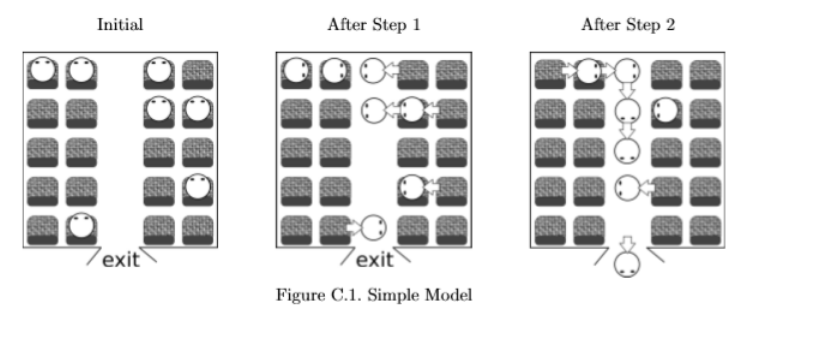
正方向顺序考虑不太能够处理，考虑所有人都走出去后再往回退（假设倒着回去相同时间也会阻塞）。把时间降序排列，相同走出时间的人会产生冲突，此时会让等待时间++。

那么让等待时间为wait

遍历不升的时间序列，对于每一个时间(ti)都让(MAX=max(MAX,ti+wait(i)))去尝试更新答案，最后的答案就是MAX

关于为什么倒着处理是对的：假设两个时间位置(ti)和(tj)，其中(tj+wait(j)<ti)，此时时间比较小的人等待的时候不会影响后续的人。

#include<bits/stdc++.h>
#include<unordered_map>
#define ll long long
#define fastio ios::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
using namespace std;

int main()
{
    fastio;
    int n, m, p;
    cin >> n >> m >> p;
    vector<int>tim;
    int tx = n + 1, ty = m + 1;
    while (p--)
    {
        int x, y;
        cin >> x >> y;
        if (y > m)y++;
        tim.push_back(abs(tx - x) + abs(ty - y));
    }
    sort(tim.begin(), tim.end(), greater<int>());
    int wait = 0;
    int MAX = tim[0];
    for (auto i : tim)
    {
        MAX = max(i + wait, MAX);
        wait++;
    }
    cout << MAX;

    return 0;

}

---

F、What Goes Up Must Come Down

题意：给一个序列，每次操作让其中某个元素和与其相邻的元素交换位置，让你求将序列变成先不降后不升（或者全局不降或全局不升）的最小操作次数。

想题过程：思维乱搞（不会）->枚举位置跑从两侧跑LIS贪心（不对）->逆序对（忘了结论）->不会搞，我是菜狗.jpg

求逆序对的做法是对的，但仅仅是类似，因为有相同元素。对每个位置求逆序对可以用树状数组进行log的修改，log的区间查询，总复杂度nlog(maxn);

求出逆序对以后，现在就是题目的一个突破点了：对于每个数，它要么在不升的区间内，要么在不降的区间内。这样通过分别求出左侧和右侧小于等于这个元素的个数（包括其本身，因为相同元素也不需要相互交换），减去它们剩下的就是大于这个元素的元素个数，与他们每个交换一次就可以让这个元素满足条件（左侧元素和右侧元素取个min）。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define fastio ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL);
const int maxn = 1e5 + 10;
 
int t[maxn];
 
int n;
 
int lowbit(int x)
{
    return x & -x;
}
 
void add(int x)
{
    for (; x < maxn; x += lowbit(x))
        t[x] += 1;
}
 
int query(int x)
{
    int res = 0;
    while (x)
    {
        res += t[x];
        x -= lowbit(x);
    }
    return res;
}
 
int main()
{
    fastio;
    cin >> n;
    vector<int>a(n + 1);
    vector<int>res(n + 1, 0);
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        add(a[i]), res[i] = i - query(a[i]);
    }
    ll ans = 0;
    memset(t, 0, sizeof(t));
    for (int i = n, j = 1; i >= 1; i--, j++)
        add(a[i]), ans += min(j - query(a[i]), res[i]);
    cout << ans << endl;
 
    return 0;
 
}