[LeetCode] 32. Longest Valid Parentheses (hard)

原题链接

题意：
寻找配对的（），并且返回最长可成功配对长度。

思路
配对的()必须是连续的，比如()(()，最长长度为2；()()，最长长度为4。

解法一 dp:
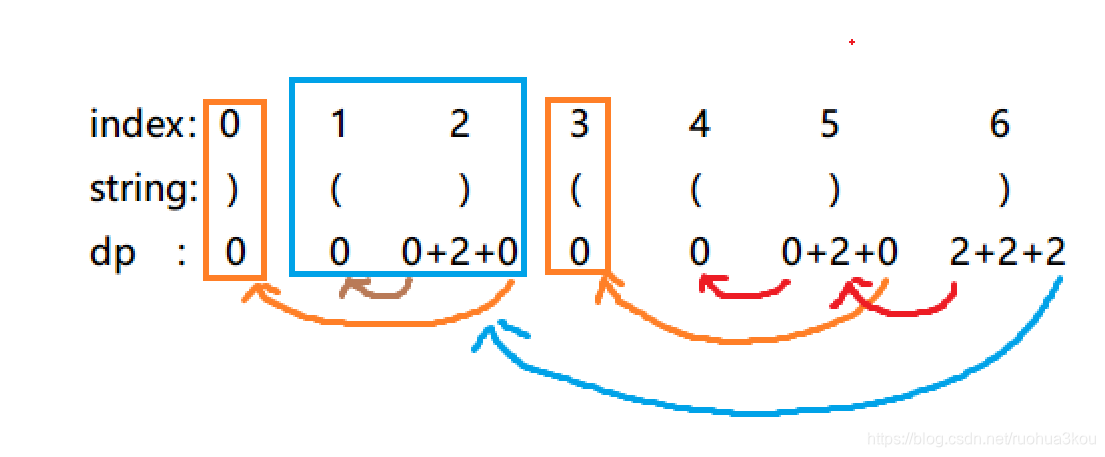
利用dp记录以s[i]为终点时，最长可配对长度。
仅当遍历到s[i]==’)'的时候记录。

dp[i]=dp[i-1]+2 		加上当前组其他对的长度
dp[i]+=dp[i-dp[i]]   		加上邻近的上一组的总长度

class Solution {
 public:
  int longestValidParentheses(string s) {
    int len = s.length();
    if (len < 2) return 0;
    vector<int> dp(len, 0);
    int res = 0;
    for (int i = 1; i < len; i++) {
      if (s[i] == ')') {
        if (s[i - 1 - dp[i - 1]] == '(')  // 判断当前')'有没有相对应位置的'('
          dp[i] = dp[i - 1] + 2; // 如果有：则当前小组数量增加
        dp[i] += dp[i - dp[i]];  // 加上上一个小组记录的数量
      }
      res = max(res, dp[i]);
    }
    return res;
  }
};

解法二 栈:
用栈去存储"(“的索引位置。
遍历字符串，
当前符号为”(“时，加入栈；
当前符号为”）"时，弹出栈顶元素，并进行判断：
——>当栈为空：说明当前所有匹配都匹配成功，长度为i+1；（i从0开始计）
——>当栈不为空：长度为max(answer,i-stack.top())

class Solution {
 public:
  int longestValidParentheses(string s) {
    int res = 0;
    int len = s.length();
    stack<int> sta;
    for (int i = 0; i < len; i++) {
      if (!sta.empty() && s[i] == ')' && s[sta.top()] == '(') {
        sta.pop();
        if (sta.empty())
          res = i + 1;
        else
          res = max(res, i - sta.top());
      } else {
        sta.push(i);
      }
    }
    return res;
  }
};