散射介质环境中偏振成像图像的去散射方法

Polarization-based vision through haze

Yoav Y.Schechner,Srinivasa G.Narasimhan,and Shree K.Nayar

Columbia University

1，介绍

         这篇文章在分析图像形成的过程中，将偏振对大气散射的影响考虑在内，然后设计从图像中去雾的算法。这个方法可以通过旋转偏振片到不同的角度或者两张偏振图像来实现。这个方法效果很好，不需要依赖天气情况的变化。

2，基本原理

        把从光源到分布粒子的光线和从分布粒子到相机的光线构成的平面作为标准平面。将一束光线分成两个偏振分量，平行的量和垂直的量。光线和此平面平行的偏振量为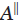，光线和此平面垂直的偏振量为，可以定义偏振度为：

 

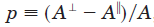
其中A定义为： 

 

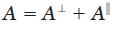
        根据大气散射模型，直接传输定义为：

 

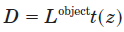
其中表示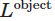无雾图像，t(z)可以表达为：

 

         从而没有经过偏振片的含雾图像可以表达为：

 

         当旋转偏振片时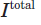，是随偏振角度变化的函数，其函数曲线如下：

   由上图可见，当偏振角度为90度时，为“最坏的状态”。当偏振角度为0度时，为“最好的状态”。其表达式如下：

 

 

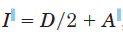
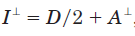
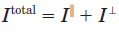
其中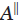和通过反解上式可得：

 

 

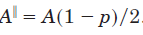
3，去雾过程

          首先，应该求得大气光值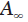和其对应的偏振度p。实验中，采取手动估计的方法，即手动选取两幅正交偏振图像的同一区域，计算该区域的每一个像素处的大气光值和对应偏振度的值，然后取这些计算值的平均值，即可得到大气光值和偏振度值。

          现在定义每一个像素点的大气光为：

 

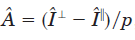
         无偏振图像为：

 

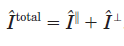
        传输函数为：

 

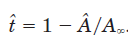
        由以上各式，得到去雾图像为：

 

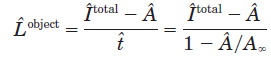
4，实现过程

     依据上述的理论过程，利用MATLAB实现其算法如下（代码中用到了guidedfiter函数，即导向滤波，可自行寻找其代码，此处省略）：

clear all;
Iper=imread('E:yycodeImageWorst_tiff16.tiff');
Ipar=imread('E:yycodeImageBest_tiff16.tiff');

N=255*255;
Ipar=double(Ipar)/N;Iper=double(Iper)/N;
Itotal=Ipar+Iper;

[m,n,o]=size(Ipar);

[Ipar_infi,rect1]=imcrop(Ipar);
Iper_infi=imcrop(Iper,rect1);

Pr=(sum(sum(Iper_infi(:,:,1)))-sum(sum(Ipar_infi(:,:,1))))/(sum(sum(Iper_infi(:,:,1)))+sum(sum(Ipar_infi(:,:,1))));
Pg=(sum(sum(Iper_infi(:,:,2)))-sum(sum(Ipar_infi(:,:,2))))/(sum(sum(Iper_infi(:,:,2)))+sum(sum(Ipar_infi(:,:,2))));
Pb=(sum(sum(Iper_infi(:,:,3)))-sum(sum(Ipar_infi(:,:,3))))/(sum(sum(Iper_infi(:,:,3)))+sum(sum(Ipar_infi(:,:,3))));

P=zeros(1,3);P(1)=Pr;P(2)=Pg;P(3)=Pb;
A=zeros(m,n,o);R=zeros(m,n,o);
for k=1:3
    A(:,:,k)=(Iper(:,:,k)-Ipar(:,:,k))/P(k);
end

x=A(:,:,1);y=A(:,:,2);z=A(:,:,3);

Ainf=zeros(1,3);
[m1,n1,o1]=size(Ipar_infi);
Ainfr=(sum(sum(Iper_infi(:,:,1)))+sum(sum(Ipar_infi(:,:,1))))/(m1*n1);
Ainfg=(sum(sum(Iper_infi(:,:,2)))+sum(sum(Ipar_infi(:,:,2))))/(m1*n1);
Ainfb=(sum(sum(Iper_infi(:,:,3)))+sum(sum(Ipar_infi(:,:,3))))/(m1*n1);

Ainf(1)=Ainfr;Ainf(2)=Ainfg;Ainf(3)=Ainfb;

t=zeros(m,n,o);
for k=1:3
    t(:,:,k)=max(1-(A(:,:,k)/Ainf(k)),0.1);
end

r=60;eps=10^-6;
for k=1:3
    t(:,:,k)=guidedfilter(Itotal,t(:,:,k),r,eps);
end

for k=1:3
    R(:,:,k)=(Itotal(:,:,k)-A(:,:,k))./(t(:,:,k));
end

imshow(R);
imwrite(R,'E:yycodeR.png');

5，实验结果

     0度偏振图像和90度偏振图像分别为：

                                               

其复原结果如下：

                                                                                                      

     可以看到，复原结果中的天空区域出现了大量的噪声，作者的其余几篇文章中有介绍去噪的方法，可是其算法的公式太过复杂，不管你会不会，我反正是不会了，希望有能力的大佬对复原结果作进一步的去噪处理，得出更好的复原结果。

Underwater polarimetric imaging for visibility enhancement utilizing active unpolarized illumination

Liming Yang, Jian Liang, Wenfei Zhang, Haijuan Ju, Liyong Ren, Xiaopeng Shao

西安电子科技大学

       下面介绍西电邵晓鹏教授团队的一种水下散射环境下的偏振成像图像去散射方法。文章认为造成水下成像图像模糊的原因主要有两个：来自水下目标物的辐射光在传输时受到水中粒子的吸收和散射作用，其在进入成像设备时形成目标辐射光的衰减光；另一部分是水下环境光受到水中粒子散射作用而形成背景光，相当于在水下目标物前面放置了一层“幕布”，这是导致水下图像中目标物难以辨认的主要原因。其实，水下散射环境比大气散射环境要复杂的多，因此造成水下成像模糊的原因也更加复杂。例如，目标辐射光在向成像系统传输时受到粒子的散射作用而形成前向散射光，这是造成水下成像图像模糊的另一个重要的原因。但是，一方面为了计算简便，另一方面前向散射相比于后向散射对图像的影响较小，所以在对水下图像进行目标复原时忽略前向散射等因素。

       通常，一幅水下图像可如下描述：

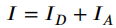
 其中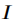，表示成像图像的总光强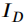，表示经过衰减的目标辐射光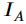，表示后向散射光，即背景光。目标辐射光和后向散射光可进一步详细地描述为：

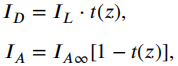
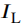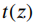其中，表示未经衰减和散射的目标辐射光，表示水下环境中景深无穷远处的光强，表示描述光强衰减过程的衰减函数。

       根据以上公式，可以推导未经衰减和散射的目标辐射光可利用相关参量表述为：

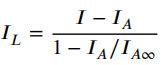
由此可得，恢复未经衰减和散射的目标辐射光的关键即为能够较为准确地估计参量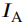和。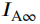

       文中采用4幅不同偏振角度的偏振图像计算斯托克斯矢量，本次实验采用不同的实验数据代替。通过FLUXDATA偏振相机拍摄某一水下场景的偏振图像。FLUXDATA偏振相机为分光型偏振相机，其成像原理是将入射到相机镜头的光用分光棱镜分成三路，在每一路放置不同的角度的偏振片以获得不同角度的偏振图像。本次实验的FLUXDATA偏振相机的偏振片方向分别为0度，60度和120度，以此获得三个不同角度的水下偏振图像、和。

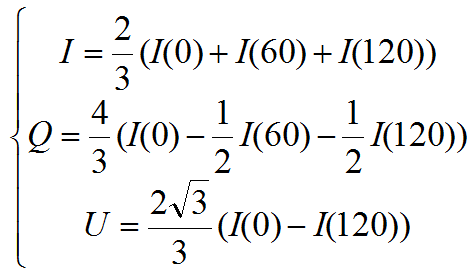
       根据解算得到的斯托克斯矢量，可计算偏振度图像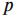和偏振角图像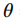如下：

       得到斯托克斯矢量中的I,Q和U后，即可依据斯托克斯公式计算每一个偏振角度下的偏振图像，则偏振图像的光强随着角度呈三角函数曲线变化，曲线的最低点对应光强最小的偏振图像，曲线的最高点对应光强最大的偏振图像，偏振图像的光强随着角度变化的曲线如下图所示：

       接下来由最大光强和最小光强的偏振图像计算背景区域的偏振度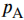，本次实验的方法是手动选取两幅正交偏振图像的无目标区域，计算该区域中每一点像素的偏振度，然后取这些偏振度值的平均值，即可得到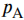。对于背景区域偏振角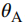的估计，文中这样解释并计算：因为偏振角图像的公式中不包含斯托克斯矢量中的光强分量，因此利用偏振角图像可以更好地估计背景光。将偏振角图像作关于角度的直方图分布，取直方图中出现概率最大的角度作为的估计值。

       定义最大光强和最小光强的角度方向分别为x轴和y轴（最大光强和最小光强对应的两个角度正交），则背景光的偏振强度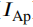在x轴和y轴的分量分别表示如下：

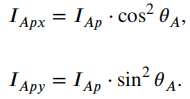两者还可如下表述：

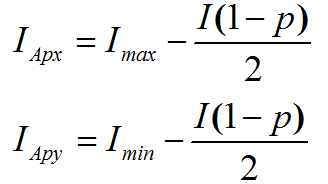
则推得为：

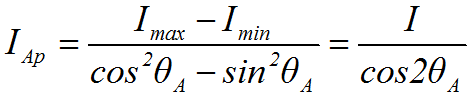
则最终推出背景光的表达式为：

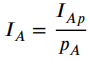
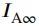         由于多次散射效应最终成为无偏光，而为具有偏振度为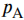的部分偏振通道光，所以可重新表达为：

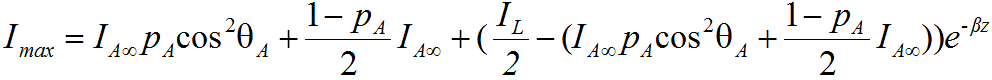
         如果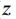取无穷大，则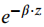趋向于0，所以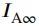可表示为：

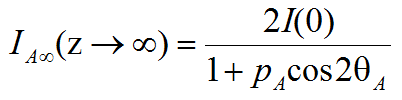
         计算得到后，取该图像灰度值最大的0.1%像素处的灰度值的平均值作为的估计值。将上述估计得到的参量代入到水下成像模型之中，即可复原出清晰的水下目标图像。

         下面通过水下偏振图像数据进行实验，并得出复原结果，以此验证本文算法的有效性。本次实验中使用的三个角度的水下偏振图像如下（从左至右分别为0度、60度和120度的水下偏振图像）：

                                                  

         首先，利用FLUXDATA偏振相机获得的0度，60度和120度三个角度的偏振图像计算斯托克斯矢量中的I,Q和U分量，并计算偏振角图像AOP，并对偏振角图像作直方图，取直方图中峰值最大值作为的估计值。实现该过程的MATLAB代码如下：

clear all;
%读入图像
image0 = imread('C:UserszihangDesktopaopcoin0.bmp');
image60 = imread('C:UserszihangDesktopaopcoin60.bmp');
image120 = imread('C:UserszihangDesktopaopcoin120.bmp');
I0 = double(image0);
I60 = double(image60);
I120 = double(image120);
I0 = I0 / 255; I60 = I60 / 255; I120 = I120 / 255;

%利用stocks矢量方法表示偏振态
I = 2 * (I0+I60+I120) / 3; 
Q = 2 * (2 * I0 - I60 - I120) / 3;
U = 2 * (I60 - I120) / sqrt(3);
DOP = sqrt(Q.^2+U.^2) ./ I;
AOP = 0.5 * (atan(U./Q));

imhist(AOP);
axis([0,1,0,120000]);

           得到的AOP的直方图如下：

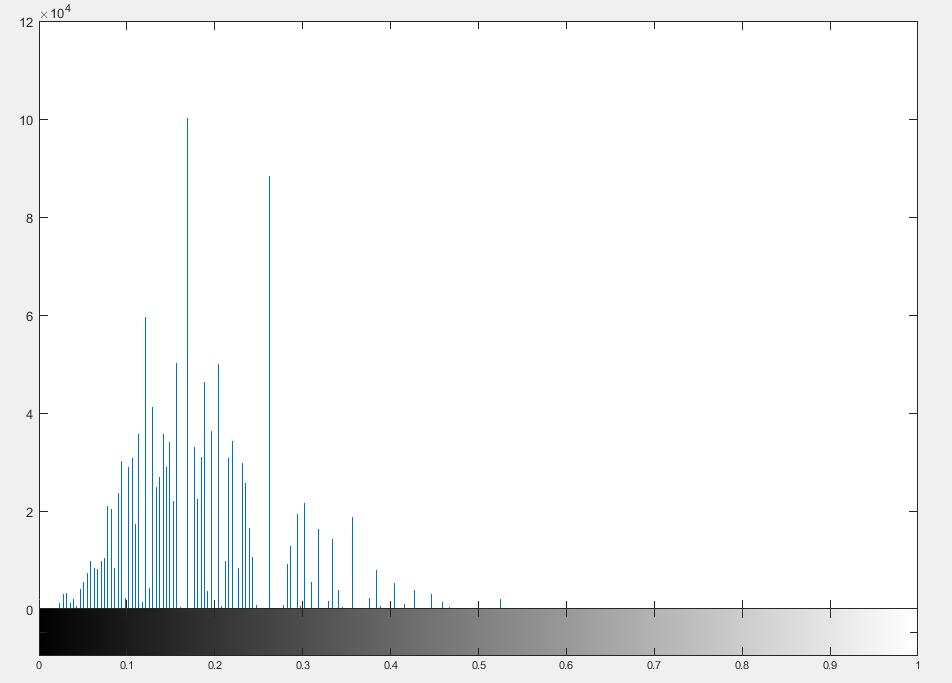
           观察该组数据对应的直方图，其大概在0.167左右取得峰值，所以该组数据对应的的估计值为0.167。

          接着由三个角度的偏振图像计算每个角度下的偏振图像，实验中选取步长为1度，遍历180个角度，并比较每一个角度下的光强，则光强最大的那幅图像为，光强最小的那幅图像为。再依据上述算法公式估计各个分量，进而复原出目标图像（对于背景区域偏振度的估计，本次实验采取了手动估计的方法），复原目标部分的代码如下：

%求解I_max,I_min
[m,n,o] = size(I);
degree = 0:1:180;
sumI = zeros(1,length(degree));
I_sum = zeros(1,length(degree));
for i = 1:length(degree)
    image = (I + Q * cos(2 * (degree(i) * pi / 180)) + U * sin(2 * (degree(i) * pi / 180))) / 2;
    sumI(i) = sum(sum(image));
    I_sum(i) = sumI(i) / (m * n);
end

[min_val, min_index] = min(I_sum);%找出最小光强值点的位置(归一化光强值，横坐标)
min_degree = degree(min_index);

[max_val, max_index] = max(I_sum);%找出最大光强值点的位置(归一化光强值，横坐标）
max_degree = degree(max_index);

Imax = (I + Q * cos(2 * (max_degree * pi / 180)) + U * sin(2 * (max_degree * pi / 180))) / 2;
Imin = (I + Q * cos(2 * (min_degree * pi / 180)) + U * sin(2 * (min_degree * pi / 180))) / 2;

theta = 0.167;
Iap = Q / (cos(2 * theta));

[m,n] = size(I);
[regionI,rect] = imcrop(I);
regionImax = Imax(floor(rect));
regionImin = Imin(floor(rect));
[hei,wid] = size(regionI);
numpx = hei*wid;
I_sum = sum(regionI(:));
I_max = I_sum/numpx;
Pa = (sum(regionImax(:)) - sum(regionImin(:))) / (sum(regionImax(:)) + sum(regionImin(:)));

Ia = Iap / Pa;
Iainf = (2 * Imax) / (1 + Pa * cos(2 * theta));

imsize = m * n;
numpx = floor(imsize / 1000);
Iainf_vec = reshape(Iainf, imsize, 1);
[Iainf_vec, indices] = sort(Iainf_vec);
indices = indices(imsize-numpx+1 : end);
atmSum=0;
for ind=1 : numpx
    atmSum=atmSum+Iainf_vec(indices(ind));
end
Iinf = atmSum / numpx;

t = ones(m,n) - Ia ./ Iinf;
recover = (I - Ia) ./ t;

figure;
imshow(recover);

           现将复原结果和光强图像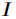进行对比，分析本文算法的有效性：

                                         

           通过上述实验对比，可以看到目标能够较为清晰的复原出来，且目标物上的图标和字迹清晰可辨。缺点是复原结果中目标物的边缘地带出现了大量噪声，为了获得更好的复原结果，可做进一步的去噪等处理。