扩展欧几里得算法

偶遇知乎dalao讲解exgcd 感觉解释的很好懂，故转载。
原帖链接：https://www.zhihu.com/question/30067108/answer/153440477


对于正整数(纠正，不是非负整数) a，b，gcd（a，b）表示 a，b 的最大公约数，必然存在整数对 x，y ，使得
a*x+b*y = gcd(a , b);     ①
根据欧几里德原理

gcd(a , b) = gcd(b , a mod b)

将gcd(b,a mod b)表达为①式的形式，即
   a*x+b*y = gcd(a , b)               
= gcd(b , a mod b)              
= b * x1 + (a mod b) * y1             
= b * x1 + (a - a / b * b) * y1   
即a*x+b*y = b * x1 + (a - a / b * b) * y1

化简上式，得a*x+b*y = a*y1 - b*a/b*y1 + b*x1

即   a * x  + b * y=  a * y1 + b  * (x1-a/b*y1)
所以x=y1y=x1 - a/b*y1
于是我们得到了这样一段代码

void exgcd(int a, int b, int &d, int &x ,int  &y)
{
    if ( !b )
    {
        d = a;
        x = 1;
        y = 0;
        return;
    }
    int x1,y1;
    exgcd( b , a % b , d , x1 , y1 );
    x = y1;
    y = x1 - ( a / b ) * y1;
    return ;
}        

有了推理过程，这段代码比题主的那一段要更加好理解但是细想其实等价于题主的代码，只是在传递参数的时候交换了 x 和 y 的位置

void exgcd(int a, int b, int &d, int &x,int &y)
{
    if(!b)
    {   
        d = a;
        x = 1;
        y = 0;
        return;
    }
    exgcd(b , a%b , d , y , x);
    y-=a/b*x;
}

上面是求 ax + by = gcd（a,b） 的一组解。

那么对于任意方程 ax + by = c 呢？

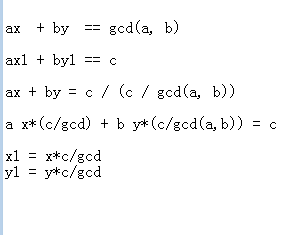
从上面可以看到，只要把求出来的 x 和 y 乘上一个 c/gcd 就可以了。

c%gcd(a,b) != 0时，方程无解。