首先膜一发网上的题解。大佬们tql。
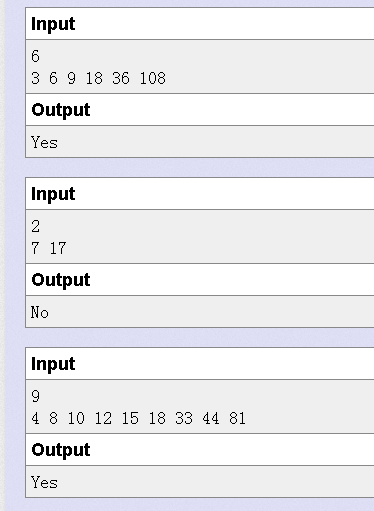
给你n个单调递增的数字,问是否能够把这些数字重新构成一棵二叉搜索树(BST),且所有的父亲结点和叶子结点之间的gcd > 1?
这个题场上是想暴力试试的。结果不行。发现符合最优子结构,可以DP。但是想不出来怎么转移。
看了大佬的题解。
若以第 k 个结点为根节点,用 L[i][k] 表示是否能够向左延伸到 i 点,R[k][j] 表示是否能够向右延伸到 j 点。
那么区间 [l, r] 合法,仅当 L[l][k] && R[k][r] == 1。
这样有了断点 k 作为[l, r]的根,就可以判断gcd能否用L[l][r] 和 R[l][r] 更新 R[l-1][r] 和 L[l][r+1]。
判断gcd可以预处理。
这样总复杂度是n^2 * logn
#include <cstdio> #include <algorithm> #include <cmath> #include <iostream> using namespace std; typedef long long LL; const int maxn = 700 + 10; int n; int a[maxn]; int v[maxn][maxn], L[maxn][maxn], R[maxn][maxn], C[maxn][maxn]; int dp[maxn][maxn][2]; int main() { scanf("%d", &n); for (int i = 1; i <= n; i++) { L[i][i] = R[i][i] = 1; scanf("%d", &a[i]); } for (int i = 1; i <= n; i++) for (int j = i+1; j <= n; j++) v[i][j] = v[j][i] = __gcd(a[i], a[j]) != 1; int r; for (int len = 1; len <= n; len++) for (int l = 1; (r = l+len-1) <= n; l++) for (int k = l; k <= r; k++) if (L[l][k] && R[k][r]) { C[l][r] = 1; if (v[k][l-1]) R[l-1][r] = 1; if (v[k][r+1]) L[l][r+1] = 1; } printf("%s ", C[1][n]?"Yes" : "No"); }