HDU 3306 Another kind of Fibonacci(矩阵+ll超时必须用int&输入必须取模&M必须是int类型)

Another kind of Fibonacci

【题目链接】Another kind of Fibonacci

【题目类型】矩阵+ll超时必须用int&输入必须取模&M必须是int类型

&题解：

算出矩阵的每一行一定要和初始化的那个矩阵不一样,如果有一项是一样的,那么就推不出最后的答案,所以矩阵如下:

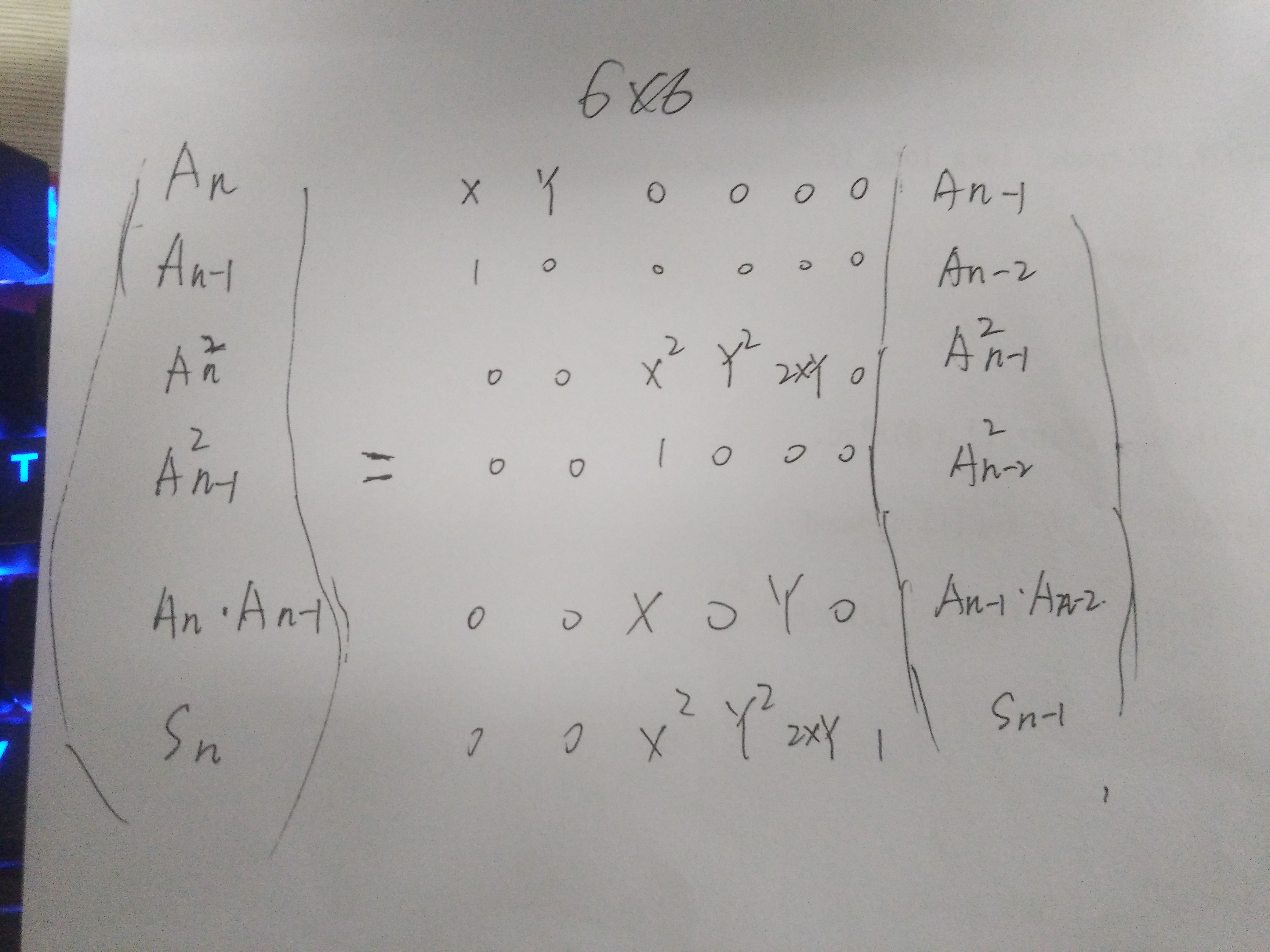
代码还有问题,T了,不知道为什么,明天在看吧

【时间复杂度】(O(logn))

&超时代码：

#include <cstdio>
#include <bitset>
#include <iostream>
#include <set>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <map>
#include <queue>
#include <vector>
using namespace std;
#define INF 0x3f3f3f3f
typedef long long ll;
const int si= 6;
struct mat
{
	ll m[si][si];
}A;
ll n,x,y,M=10007;
mat Mul(mat a,mat b)
{
	mat c;
	for(int i=0;i<si;i++)
		for(int j=0;j<si;j++){
			c.m[i][j]=0;
			for(int k=0;k<si;k++)
				c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j])%M;
		}
	return c;
}
mat bPow(mat a,ll z)
{
	mat un;
	for(int i=0;i<si;i++)for(int j=0;j<si;j++)
		un.m[i][j]=(i==j);
	while(z){
		if(z&1)
			un=Mul(un,a);
		a=Mul(a,a);
		z>>=1;
	}
	return un;
}
ll tb[si];
void Init()
{
	for(int i=0;i<5;i++)tb[i]=1;
	tb[5]=2;
	memset(A.m,0,sizeof(A.m));
	A.m[0][0]=x,A.m[0][1]=y;
	A.m[1][0]=1;
	A.m[2][2]=x*x,A.m[2][3]=y*y,A.m[2][4]=2*x*y;
	A.m[3][2]=1;
	A.m[4][2]=x,A.m[4][4]=y;
	for(int i=0;i<si;i++) A.m[5][i]=A.m[2][i];
	A.m[5][5]=1;
}
void DF(mat a)
{
	for(int i=0;i<si;i++){
		for(int j=0;j<si;j++)
			cout<<a.m[i][j]<<" ";
		cout<<endl;
	}
}
int main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	freopen("E:1.txt","r",stdin);
	while(cin>>n>>x>>y){
		x%=M,y%=M;
		Init();
//		DF(A);
		ll ans=0;
		if(n==0){
			cout<<1<<endl;
		}
		else if(n==1){
			cout<<2<<endl;
		}
		else{
			A=bPow(A,n-1);
//			DF(A);
			for(int i=0;i<si;i++){
				ans=(ans+A.m[5][i]*tb[i])%M;
			}
			cout<<ans<<endl;
		}
	}
	return 0;
}

&题解2：

妈的,这题真tm智障,花了我2个小时,最后终于对照别人ac代码找到了错误.
注意1:矩阵中是long long 类型 运算没有int快 所以要改为int型 还有取模的M也必须要是int型 如果M是ll的话也会超时.
注意2:相应地,上面由long long改为int了 所以输入数据必须要取模了
总结:好智障的烂题啊,居然卡在数据类型上.(当然,也应该注意一下了:能用int的就不要用long long,因为如果用了long long 就有可能超时;原来一直以为用ll不会爆范围,就总是用ll,现在发现了,一直用ll会爆时间,尤其是在这种矩阵快速幂的题里,绝对要注意!!!)

&AC代码：

#include <cstdio>
#include <bitset>
#include <iostream>
#include <set>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <map>
#include <queue>
#include <vector>
using namespace std;
#define INF 0x3f3f3f3f
typedef long long ll;
const int si= 6;
struct mat
{
    int m[si][si];
}A;
ll n,x,y;
int M=10007;
mat Mul(mat a,mat b)
{
    mat c;
    for(int i=0;i<si;i++)
        for(int j=0;j<si;j++){
            c.m[i][j]=0;
            for(int k=0;k<si;k++)
                c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j])%M;
        }
    return c;
}
mat bPow(mat a,ll z)
{
    mat un;
    for(int i=0;i<si;i++)for(int j=0;j<si;j++)
        un.m[i][j]=(i==j);
    while(z){
        if(z&1)
            un=Mul(un,a);
        a=Mul(a,a);
        z>>=1;
    }
    return un;
}
ll tb[si];
void Init()
{
    for(int i=0;i<5;i++)tb[i]=1;
    tb[5]=2;
    memset(A.m,0,sizeof(A.m));
    A.m[0][0]=x,A.m[0][1]=y;
    A.m[1][0]=1;
    A.m[2][2]=x*x%M,A.m[2][3]=y*y%M,A.m[2][4]=2*x*y%M;
    A.m[3][2]=1;
    A.m[4][2]=x,A.m[4][4]=y;
    for(int i=0;i<si;i++) A.m[5][i]=A.m[2][i];
    A.m[5][5]=1;
}
void DF(mat a)
{
    for(int i=0;i<si;i++){
        for(int j=0;j<si;j++)
            cout<<a.m[i][j]<<" ";
        cout<<endl;
    }
}
int main()
{
    while(cin>>n>>x>>y){
        x%=M,y%=M;
        Init();
        ll ans=0;
        if(n==0){
            cout<<1<<endl;
        }
        else if(n==1){
            cout<<2<<endl;
        }
        else{
            A=bPow(A,n-1);
            for(int i=0;i<si;i++){
                ans=(ans+A.m[5][i]*tb[i])%M;
            }
            cout<<ans<<endl;
        }
    }
    return 0;
}