UVA 503 Parallelepiped walk

https://vjudge.net/problem/UVA-503

题目

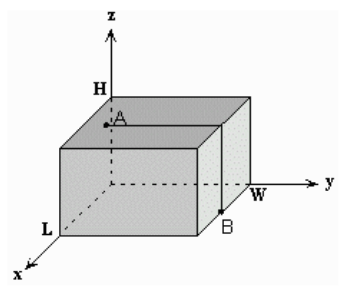
 给出一个长方体和长方体上两点的坐标，求两点的沿着长方体表面走的最小距离

题解

沿着表面走就是在展开图上面走，如果分类讨论就需要考虑很多情况，比如两个相邻的面、相对的面，有时候需要走4个展开面，有时候要走3个，是不是走的面越多距离越长，这些都说不清楚……而且手动写出所有情况很麻烦……

于是只有选择模拟展开这个长方体了，需要考虑很多细节，比如给面编号，把每个点对应到面的坐标找出来，然后还要判断走展开图是否不会超出每个面

这时我写过的最长的模拟了……

AC代码

#include<cstdio>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<cstring>
#include<vector>
#include<cassert>
#include<map>
#include<string>
using namespace std;
#define REP(r,x,y) for(register int r=(x); r<y; r++)
#define REPE(r,x,y) for(register int r=(x); r<=y; r++)
#ifdef sahdsg
#define DBG(...) printf(__VA_ARGS__)
#else
#define DBG(...) (void)0
#endif

#define MAXN 10007
int l,w,h;
inline int calc(int a, int b) {return a*a+b*b;}
inline int tabs(int x) {return x<0?-x:x;}
#define LL long long
template <class T, int z>
struct A{
	T data[z];
	int n;
	A():n(0) {}
	T& operator[](int q) {return data[q];}
	inline void push(T x) {data[n++]=x;}
	inline T& pop() {return data[--n];}
};
#define EPS 1e-6
inline int dcmp(double x) {return fabs(x)<EPS?0:(x<0?-1:1);}
#define D Point
#define CD const D
struct Point {
	double x,y;
};
struct Box {
	int x,y,w,h;
};
D operator-(CD&l, CD&r) {return (D){l.x-r.x,l.y-r.y};}
D operator+(CD&l, CD&r) {return (D){l.x+r.x,l.y+r.y};}
D operator*(CD&l, double r) {return (D){l.x*r, l.y*r};}
bool operator<(CD&l, CD&r) {
	return dcmp(l.x-r.x)<0 ||
		(dcmp(l.x-r.x)==0 && dcmp(l.y-r.y)<0);
}
double cross(CD&l, CD&r) {return l.x*r.y-l.y*r.x;}
double dot(CD&l, CD&r) {return l.x*r.x+l.y*r.y;}
bool onseg(CD&p, CD&a, CD&b) {
	return dcmp(cross(a-p,b-p))==0&&dcmp(dot(a-p,b-p))<0;
}
bool segsec(CD&a, CD&b, CD&c, CD&d) {
	if(onseg(a,c,d) || onseg(b,c,d) || onseg(c,a,b) || onseg(d,a,b)) return 1;
	double c1=cross(b-a,c-a), c2=cross(b-a,d-a), c3=cross(d-c,a-c), c4=cross(d-c,b-c);
	return dcmp(c1)*dcmp(c2)<0 && dcmp(c3)*dcmp(c4)<0;
}
D intersec (CD&a, CD&b, CD&c, CD&d) {
	D v=b-a,w=d-c,u=a-c;
	double t=cross(w,u)/cross(v,w);
	return a+v*t;
}
bool inbox(D p, Box&r) {
	p.x-=r.x,p.y-=r.y;
	return dcmp(p.x)>=0 && dcmp(p.x-r.w)<=0 && dcmp(p.y)>=0 && dcmp(p.y-r.h)<=0;
}
#undef D
#undef CD
inline int id(int x, int y, int z) {
	if(x==l) return 0;
	if(y==0) return 1;
	if(y==w) return 2;
	if(z==h) return 3;
	if(z==0) return 4;
	//if(x==0) ans=5;
	return 5;
}
struct P {
	int x,y,z;
	int id;
	int dx,dy;
} p,q;
const int way[6][6]={
	{0,1,2,3,4,5}, {1,5,0,3,4,2}, {2,0,5,3,4,1}, {3,1,2,5,0,4}, {4,1,2,0,5,3}, {5,2,1,3,4,0}
};
const int *len[6][4]={
	{&h,&h,&w,&w}, {&h,&h,&l,&l}, {&h,&h,&l,&l}, {&l,&l,&w,&w}, {&l,&l,&w,&w}, {&h,&h,&w,&w}
};
inline void task1(int x,int y, int z, int id, int&dx, int &dy) {
	switch(id) {
		case 0: dx=y,dy=h-z;break;
		case 1: dx=x,dy=h-z;break;
		case 2: dx=l-x,dy=h-z;break;
		case 3: dx=y,dy=x;break;
		case 4: dx=y,dy=l-x;break;
		case 5: dx=w-y,dy=h-z;break;
	}
}
bool vis[6];
A<int,6> op;
int oid[6];
const int _1[]={1,5,0,3,4,2};
const int _2[]={2,0,5,3,4,1};
const int _3[]={3,1,2,5,0,4};
const int _4[]={4,1,2,0,5,3};
inline void rotateO(int x) {
	int ooid[6];
	switch(x) {
		case 1: REP(i,0,6) ooid[i]=oid[_1[i]];break;
		case 2: REP(i,0,6) ooid[i]=oid[_2[i]];break;
		case 3: REP(i,0,6) ooid[i]=oid[_3[i]];break;
		case 4: REP(i,0,6) ooid[i]=oid[_4[i]];break;
		default: assert(false);
	}
	memcpy(oid,ooid,sizeof oid);
}
const int fan[]={0            ,2,1,4,3};
bool findp() {
	if(oid[0]==p.id) return true;
	vis[oid[0]]=1;
	REPE(i,1,4) if(!vis[oid[i]]) {
		op.push(i); rotateO(i);
		if(findp()) return true;
		op.n--; rotateO(fan[i]);
	}
	vis[oid[0]]=0;
	return false;
}
void dop();
void findq(int op1, int op2) {
	if(oid[0]==q.id) {dop(); return;}
	vis[oid[0]]=1;
	if(!vis[oid[op1]]) {
		op.push(op1); rotateO(op1);
		findq(op1,op2);
		op.n--; rotateO(fan[op1]);
	}
	if(!vis[oid[op2]]) {
		op.push(op2); rotateO(op2);
		findq(op1,op2);
		op.n--; rotateO(fan[op2]);
	}
	vis[oid[0]]=0;
}
inline void turnleft(int &x,int &y,int id) {
	int nx, ny;	nx=y,ny=(*len[id][3-1])-x;
	x=nx,y=ny;
}
inline void turnright(int &x, int &y, int id) {
	int nx, ny; ny=x, nx=(*len[id][1-1])-y;
	x=nx,y=ny;
}
inline void turn180(int &x, int &y, int id) {
	int nx, ny; nx=(*len[id][3-1])-x, ny=(*len[id][1-1])-y;
	x=nx,y=ny;
}
inline void rotateP(P&x,int z) {
	const int _[]={1,5,2,0};
	const int Z[]={3,5,4,0};
	switch(z) {
		case 1:
		case 2:
			if(z==1) {
				if(x.id==3) {turnleft(x.dx,x.dy,x.id);}
				if(x.id==4) {turnright(x.dx,x.dy,x.id);}
				x.id=_2[x.id];
			}
			if(z==2) {
				if(x.id==3) {turnright(x.dx,x.dy,x.id);}
				if(x.id==4) {turnleft(x.dx,x.dy,x.id);}
				x.id=_1[x.id];
			}

			break;
		case 3:
		case 4:
			if(z==3) {
				if(x.id==1) {turnright(x.dx,x.dy,x.id);}
				if(x.id==2) {turnleft(x.dx,x.dy,x.id);}
				if(x.id==4) {turn180(x.dx,x.dy,x.id);}
				if(x.id==5) {turn180(x.dx,x.dy,x.id);}
				x.id=_4[x.id];
			}
			if(z==4) {
				if(x.id==1) {turnleft(x.dx,x.dy,x.id);}
				if(x.id==2) {turnright(x.dx,x.dy,x.id);}
				if(x.id==3) {turn180(x.dx,x.dy,x.id);}
				if(x.id==5) {turn180(x.dx,x.dy,x.id);}
				x.id=_3[x.id];
			}
			break;
		default:
			assert(false);
	}
}
inline void rotate(int x) {
	const int q[]={1,5,2,0};
	const int k[]={0,3,5,4};
	switch(x) {
		case 1:
		case 2:
			swap(l,w);
			break;
		case 3:
		case 4:
			swap(h,l);
			break;
		default:
			assert(false);
	}
}
inline void gop() {
	REP(i,0,op.n) {
		rotateP(p,op[i]); rotateP(q,op[i]);
		rotate(op[i]);
	}
	assert(p.id==0); 
}
int ans;
inline void work() {
	ans=0x7f7f7f7f;
	p.id=id(p.x,p.y,p.z), q.id=id(q.x,q.y,q.z);
	task1(p.x,p.y,p.z,p.id,p.dx,p.dy); task1(q.x,q.y,q.z,q.id,q.dx,q.dy);
	REP(i,0,6) oid[i]=i;
	memset(vis,0,sizeof vis); op.n=0; findp();
	gop();
	REP(i,0,6) oid[i]=i;
	memset(vis,0,sizeof vis); op.n=0; findq(1,3);
	memset(vis,0,sizeof vis); op.n=0; findq(2,3);
	memset(vis,0,sizeof vis); op.n=0; findq(1,4);
	memset(vis,0,sizeof vis); op.n=0; findq(2,4);
	printf("%d
", ans);
}
inline void dop() {
	int nowx=0, nowy=0; int ll=l, ww=w, hh=h;
	P pp,qq; pp=p,qq=q;
	A<int,17> px,py;
	A<Point,34> pt;
	A<Box,17> pb;
	px.push(0), py.push(0);
	px.push(*len[0][2-1]), py.push(*len[0][4-1]);
	REP(i,0,op.n) {
		pb.push((Box){nowx,nowy,*len[0][3-1],*len[0][1-1]});
		switch(op[i]) {
			case 1:
				nowx-=l; px.push(nowx);
				break;
			case 2:
				nowx+=w; px.push(nowx);
				break;
			case 3:
				nowy-=l;py.push(nowy);
				break;
			case 4:
				nowy+=h; py.push(nowy);
				break;
			default:
				assert(false);
		}
		rotateP(q,op[i]);rotate(op[i]);
	}
	pb.push((Box){nowx,nowy,*len[0][3-1],*len[0][1-1]});
	q.dx+=nowx,q.dy+=nowy;
	Point A=(Point){(double)p.dx,(double)p.dy}, B=(Point){(double)q.dx,(double)q.dy};
	sort(px.data,px.data+px.n); sort(py.data,py.data+py.n);
	pt.push(A); pt.push(B);
	REP(i,0,px.n) {
		Point D=intersec(A,B,(Point){(double)px[i],0},(Point){(double)px[i],1});
		if(onseg(D,A,B)) pt.push(D);
	}
	REP(i,0,py.n) {
		Point D=intersec(A,B,(Point){0,(double)py[i]},(Point){1,(double)py[i]});
		if(onseg(D,A,B)) pt.push(D);
	}
	sort(pt.data,pt.data+pt.n);
	REP(i,1,pt.n) {
		bool ac=false;
		REP(j,0,pb.n){
			Point x=(pt[i]+pt[i-1])*0.5;

			if(inbox((pt[i]+pt[i-1])*0.5,pb[j])) {
				ac=true; break;
			}
		}
		if(!ac) {goto _end;}
	}
	ans=min(ans,(p.dx-q.dx)*(p.dx-q.dx)+(p.dy-q.dy)*(p.dy-q.dy));
	assert(0==q.id);
_end:
	p=pp,q=qq,l=ll,w=ww,h=hh;
}

int main() {
	int cnt=0;
    #ifdef sahdsg
    freopen("in.txt","r",stdin);
    #endif // sahdsg
	while(~scanf("%d%d%d%d%d%d%d%d%d",&l,&w,&h,&p.x,&p.y,&p.z,&q.x,&q.y,&q.z)) {
		work();
	}
	return 0;
}