题目
给出P个点,然后给出Q个询问,问从P中选出两个点和给的点能组成直角三角形的方法个数。-O2,时间限制5秒。
[2leqslant Pleqslant 2000,qquad 1leqslant Qleqslant2000]
[leftlvert x_i ight vert leqslant 10^9,leftlvert y_i ight vert leqslant 10^9]
题解
卡常数的题目……刚开始想了个$n^2 imes q$的做法= =显然过不了
稍微思考就分别以P个点和Q个点为中心对P个点进行极角排序,然后分两种情况(注意Q的位置)
1、
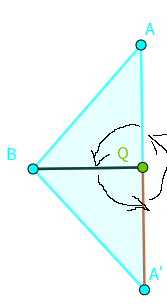
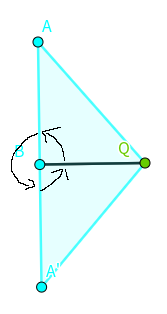
2、
对于1,可以枚举每一条与Q相连的边,然后顺时针寻找和这条边垂直的,类似于旋转卡壳,两个垂直的边会同时旋转,虽然极角排序需要$mathcal{O}(nlog n)$的时间,二分和这个比起来在渐进意义上没有改变,但是因为要卡常,所以能减少一点是一点= =
对于2,可以预处理出以P个点为中心的极角排序,然后看和Q相连的边,找直角……(可以思考下如果找到A怎么办233(反正也不会重复,找到了也没事))
那么1可以$q imes nlog n+q imes n$
2可以$q imes q log n$
因为要卡常,还需要很多技巧。
需要充分利用CPU的缓存,经常用的数据要放在一起,如果B要A的数据,C要B的数据,AAABBBCCC地做会比ABCABCABC慢,寄存快于缓存,缓存快于内存= =虽然用什么都是系统和编译器决定的,但是只有尽量放一起才能命中缓存。
对于2,$AB$和$BA'$两个垂直其实只用考虑斜率,那么在排序的时候就不用管象限了。
极角排序还是可以用斜率的,排序起来比叉乘快得多……而且比较大小也不必要非要按照分数的大小关系,只要保持有序就可以二分统计数字,这样就可以化为最简以后直接排序。
除了排序还可以将斜率进行HASH,unordered_map就可以用
(其实上面两种技巧我一个都不会= =看别人的代码卡过的)
AC代码:
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cctype>
using namespace std;
#define REP(i,a,b) for(register int i=(a);i<(b);i++)
#ifdef sahdsg
#define DBG(...) printf(__VA_ARGS__)
#else
#define DBG(...) (void)0
#endif // LOCAL
#define D Point
#define CD const D
struct Point {
long long x,y;
int k;
};
inline bool operator<(CD&l, CD&r) {
return l.x<r.x || (l.x==r.x && l.y<r.y);
}
inline D operator-(D a, D b) {
return (D){a.x-b.x, a.y-b.y};
}
#define dot(a, b) (a.x*b.x+a.y*b.y)
#define cross(a,b) (a.x*b.y-a.y*b.x)
inline int qquad(D a) {
if(a.x>0 && a.y>=0) return 1;
if(a.x<=0 && a.y>0) return 2;
if(a.x<0 && a.y<=0) return 3;
return 4;
}
inline bool cmp(D l, D r) {
if(l.k==r.k) {return cross(l,r)>0LL;}
return l.k<r.k;
}
const int T[]={0,3,4,1,2};
const int TT[]={0,2,3,4,1};
inline D rotCCW(D p) {return (D){-p.y,p.x,TT[p.k]};}
#undef D
#undef CD
#define LL long long
template<class T>
inline void read(T&x) {
x=0; int f=1; char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1; ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0'; ch=getchar();}
x*=f;
}
inline LL gcd(LL a, LL b) {
return b==0?a:gcd(b,a%b);
}
Point P[2007],A[2007];
Point Z[2007];
Point zi[2007*2];
inline int findge(Point *t, int l, int r, Point k) {
while(l<r) {
int m=l+r>>1;
if(t[m]<k) l=m+1;
else r=m;
}
return l;
}
inline int findg(Point *t, int l, int r, Point k) {
while(l<r) {
int m=l+r>>1;
if(k<t[m]) r=m;
else l=m+1;
}
return l;
}
int aaa[2007];
int main() {
int n,q; read(n); read(q);
REP(i,0,n) {
read(P[i].x); read(P[i].y);
}
REP(i,0,q) {
read(A[i].x); read(A[i].y);
}
REP(i,0,q){
REP(j,0,n) {
zi[j]=P[j]-A[i];
zi[j].k=qquad(zi[j]);
}
sort(zi,zi+n,cmp);
REP(j,0,n) zi[j+n]=zi[j];
for(register int j=0,k=0,l=0,m=0; j<n;) {
for(; k<j+n && cross(zi[j],zi[k])==0 && dot(zi[j],zi[k])>0; k++);
for(l=max(k,m); l<j+n && cross(zi[j],zi[l])>0 && dot(zi[j],zi[l])>0; l++);
for(m=max(m,l); m<j+n && cross(zi[j],zi[m])>0 && dot(zi[j],zi[m])==0; m++);
aaa[i]+=(k-j)*(m-l);
j=k;
}
}
REP(j,0,n) {
int p=0;
REP(k,0,n) if(k!=j) {
Z[p]=P[k]-P[j];
Z[p].k=qquad(Z[p]);
LL g=gcd(Z[p].x,Z[p].y);
Z[p].x/=g, Z[p].y/=g;
if(Z[p].x<0) Z[p].x*=-1, Z[p].y*=-1;
p++;
}
sort(Z,Z+p);
REP(i,0,q) {
Point z;
Point *L, *R;
z=P[j]-A[i];
int t=-z.y;
z.y=z.x; z.x=t;
LL g=gcd(z.x,z.y);
z.x/=g, z.y/=g;
if(z.x<0) z.x=-z.x, z.y=-z.y;
aaa[i]+=findg(Z,0,n-1,z)-findge(Z,0,n-1,z);
} //DBG("~~~%d
", aaa[i]);
}
REP(i,0,q) printf("%d
", aaa[i]);
return 0;
}
对了就能拿银(快哭了)