第一章 绪论
内容概要：
图灵机及RAM模型；算法复杂度评估 （不是时间，而是计算操作的次数）。
渐进分析：大O （最坏），大Θ；算法分析。
封底估算及实例 （计算大概量级）
- 1 day =10^5 s; 300 year = 10^10 s.
两种算法：迭代，递归算法
- 迭代vs递归：递归形式简介；但效率经常小于迭代。
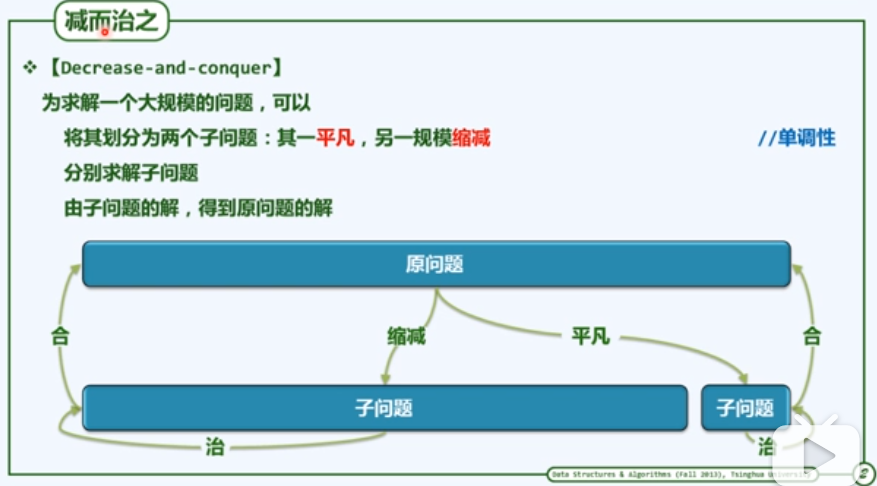
两种策略：减而治之，分而治之；结合实例，两种典型的分析的方法：递归跟踪和递推式。
动态规划:
fibonacci example, two implementation:recursive (O(2^n)) and iteration (O(n)).
LCS：待理解。
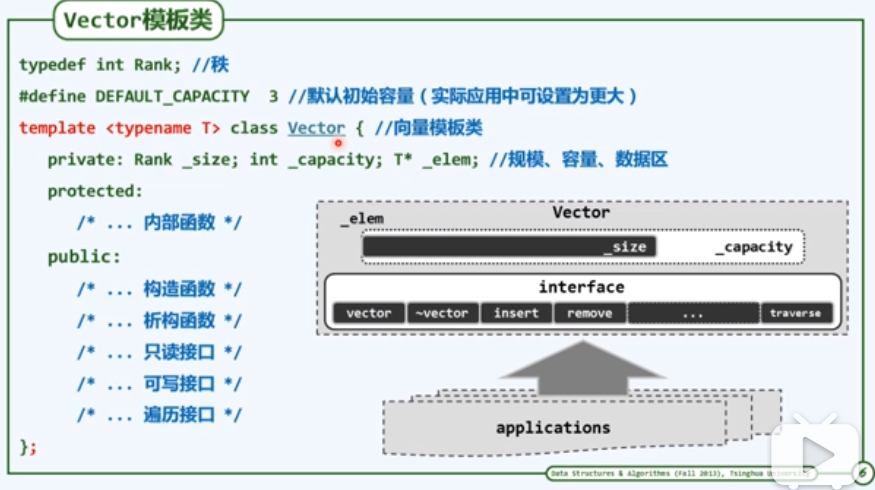
第二章 向量
向量即Vector, 与List一起，构成了最基础的顺序数据结构。
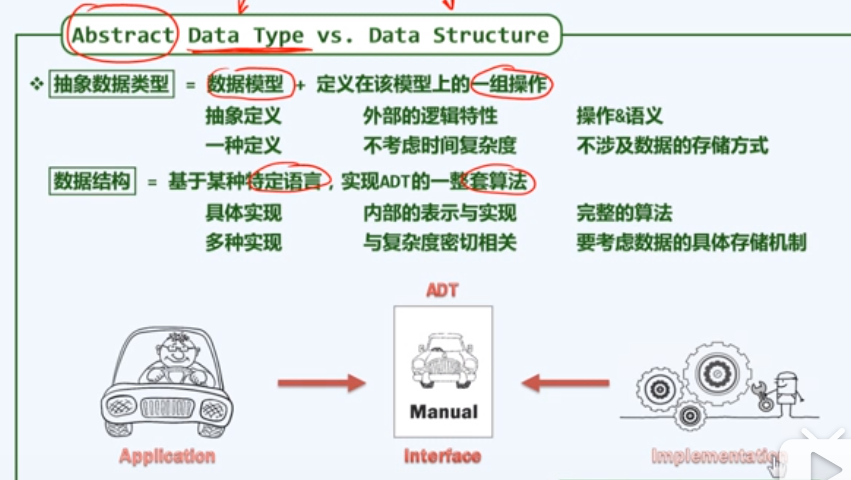
ADT v.s. Data structure, Difference?
从数组到向量：向量是基于数组结构实现的。
向量ADT接口
向量支持的操作
- 构造/析构，复制：
-
- 扩容：size 满载时double；动态内存管理的效率考虑（递增式扩容 vs. 加倍式扩容）。
- 寻秩访问：get(), put(), or 重载[ ]通过数组实现；
- 单个插入：带插入位置整体后移；区间插入：带插入位置后整体位移一定长度。
- 查找操作：对于有序向量，需支持判等操作；对于无序向量，需支持比较操作。=> 输入敏感算法。
- 单元素/区间删除：单元素删除是在调用区间删除，而不是反过来；效率考虑。
- 唯一化：用到查找和删除；复杂度：O(n^2)。
- 遍历：通过函数指针或者函数对象实现。
-
有序向量（很多操作将大大简化）：
- 唯一化，低效版 vs 高效版。
- 二分查找：复杂度1.5logn；
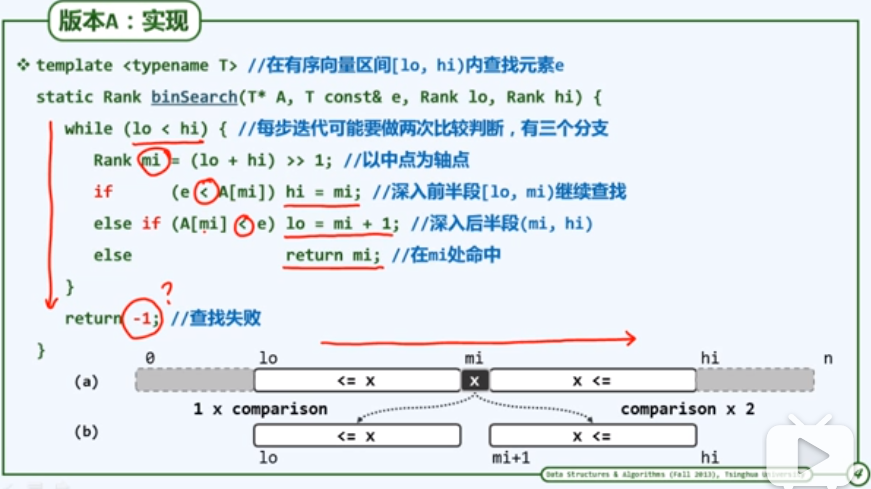
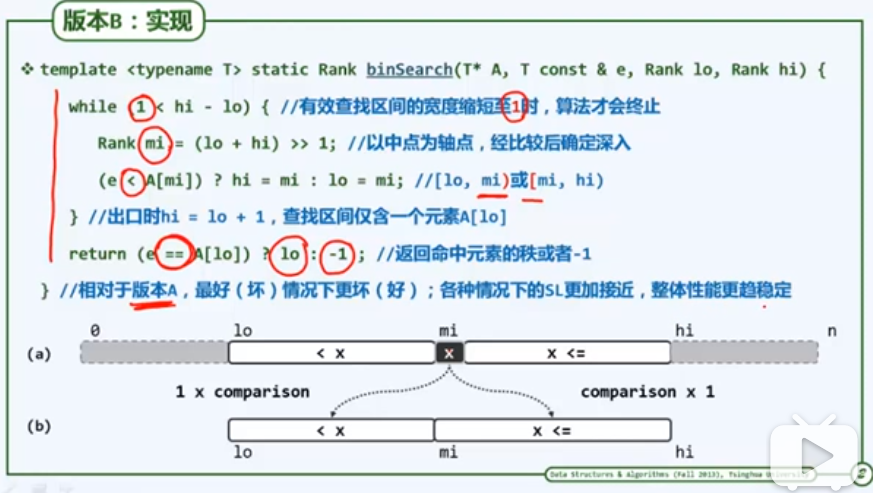
(该版本本质上在找大于e的第一个元素)
Fibonacci查找(与二分查找区别：如何切割/取划分的中点)，复杂度：1.44 logn.
起泡排序算法的两种版本：
-
- 算法复杂度：最好为O(n), 最坏为O(n^2).
归并排序
- 分治策略的典型应用；先分，再Merge。O(nlog(n))复杂度。