1, 树:兼顾动态操作与静态操作;可以认为是list<list>,半线性结构。基本概念:
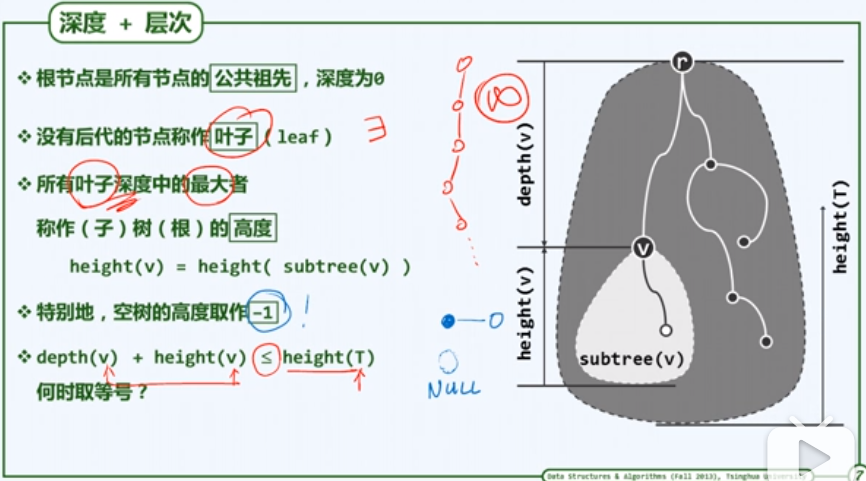
- 树的深度:每个节点到根的唯一通路所经过的边的数目,称作该节点的深度。
- 树的高度:所有节点深度的最大值称作该树的高度;任一节点对应子树的高度,称作该节点的高度。
- 节点的度数:节点v的孩子的总数,称作其度数。无孩子的节点,称为叶节点(Leaf)。
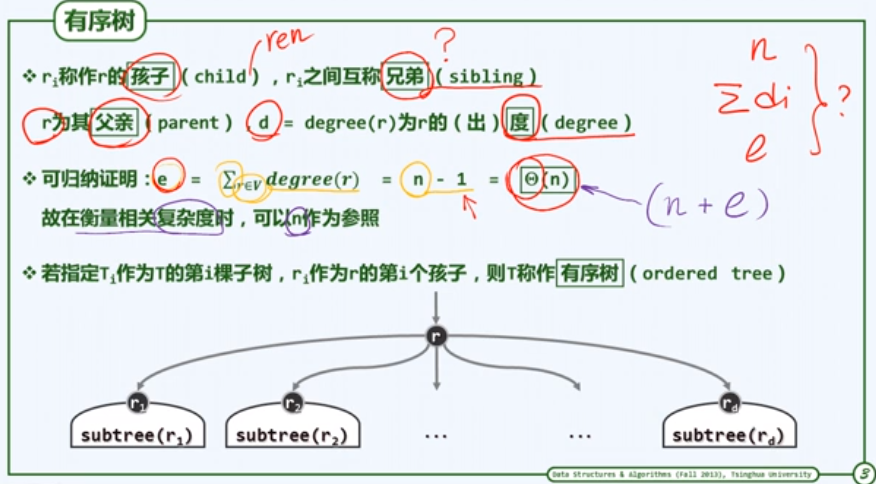
2, 有序树:
3,路径长度:边数。
4,连通图与无环图;深度层次。
5, 接口
- root()
- parent()
- firstChild()
- nextSibling()
- insert(i,e)
- remove(i)
- traverse()
6, 树的逻辑结构
- 父节点表示法:向上查找容易;向下难。
- 孩子结点表示法:向下查找容易;向上难。
- 父亲+孩子结点表示法:向上向下查找均容易;子树数目不均衡。
- 长子+兄弟表示法:很强大。
7,二叉树
- 二叉树概念
- 真二叉树:不含一度节点的二叉树
- 用二叉树表示多叉树
8,二叉树的实现:BinTree模板类
- 基本组成:BinNode模板类
- BinTree模板类
- 高度更新
- 节点插入
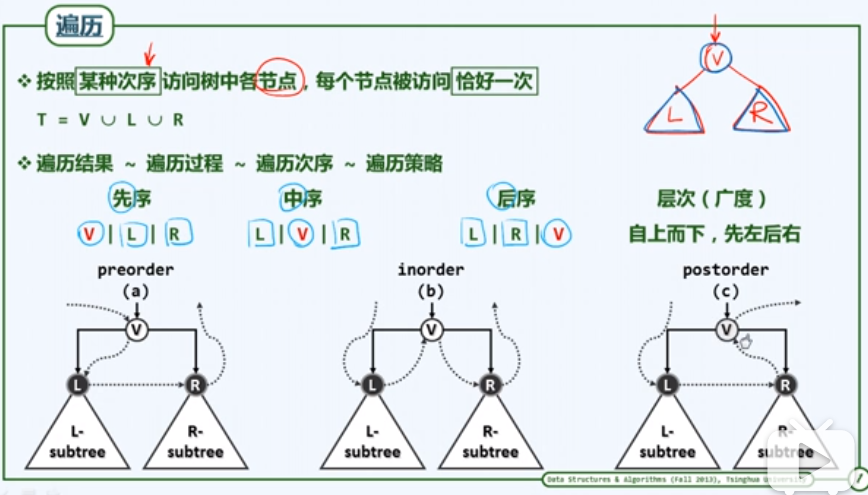
- 遍历:先序,中序,后序

9,二叉树BinTree模板类的遍历算法
- 半线性结构--> 线性结构,通过遍历完成转化。
-
先序遍历
- 递归版本
- 迭代版本1和版本2
-
中序遍历
-
递归版本:复杂度O(n).
-
递归版本:复杂度O(n).
-
-
-
后序遍历 (略)
-
层次遍历: 依靠队列(Queue)实现。
-
10, 二叉树的重构:可否由其遍历序列,还原出该二叉树?
- [先序 | 后序] + 中序 -> 二叉树
- [先序 + 后序] x 真二叉树 -> 二叉树