集成学习属于机器学习的算法模型、模型融合属于数据挖掘多个模型得到结果的融合,但他们本质是一样的都是为了使用多个基本模型来提高泛化能力。放在一起统一的讲一讲。
为什么多模型能带来更好效果呢?
《机器学习》(周志华)一书从三个角度给出了学习器的结合带来的三个好处:
从统计上来说,由于假设空间很大,可能有多个假设能在训练集达到同等最优性能(但对于测试集表现不同),若使用单个学习器可能因误选使泛化性能不佳,因此多个学习器可减少这一风险
从计算性能(最优化)来看。学习算法可能陷入局部极小,因此泛化性能不好。多学习器可降低风险
从表示的方面看,某些学习任务的真实假设可能不在当前学习算法考虑的假设空间,多个学习器则扩大来假设空间。
另外自己再添加一点:Boosting 类算法能够利用之前的基础学习器的结果,给予错误分类样本更大的权重,或者是利用残差学习。降低了模型的偏差,因此效果更好。
voting & averaging
顾名思义,最基本的融合方式 ,回归用 averaging,分类用 voting。也是很多后面的融合方式的基础
bagging
- 一种集成学习算法,基于bootstrap sampling 自助采样法,重复性有放回的随机采用部分样本进行训练最后再将结果 voting 或者 averaging 。
- 它是并行式算法,因为不同基学习器是独立
- 训练一个bagging集成学习器时间复杂度与基学习器同阶(n倍,n为基学习器个数)。
- bagging可以用于二分类/多分类/回归
- 每个基学习器的未用作训练样本可用来做包外估计,评价泛化性能。
- bagging 的原理是降低 方差。
- 两个步骤 1. 抽样训练 2 融合
典型算法:随机森林:进一步在决策树训练时加入随机属性选择。因此随机森林即有样本随机性(来自bagging的boostrap sampling)又有特征随机性。
boosting
- 一类将弱学习器提升为强学习器的算法,Boosting的思想是一种迭代的方法,每一次训练的时候都更加关心分类错误的样例,给这些分类错误的样例增加更大的权重,下一次迭代的目标就是能够更容易辨别出上一轮分类错误的样例。
- 串行。每个学习器要依赖前面训练的学习器
- 代表作: AdaBoost 、提升树、GBDT、XGBoost
- 关注于降低 偏差
- 对离群点、噪声点鲁棒性不好,因为分类错误的样例增加更大的权重
- 一般 boost 包含三要素(这里主要指加法模型与前向分布算法的boost模型,例如提升树。Adaboost也可以理解为加法模型与前向分布算法的boost模型。来自知乎用户 wps):

- 基分类器的正确率应该大于 50%
AdaBoost
用于分类!每一轮的学习器根据上一轮学习起的结果来调整样本权重(误分类样本权重越大),并根据这个学习起的效果赋予这个学习器权重。最终结果是所有学习器的加权叠加。
- AdaBoost 步骤:(0)假设样本具有均匀权值分布(1)循环迭代多次 : 使用当前加权分布学习基本分类器、计算分类器在数据集上误差率、计算分类器的系数(以供后面融合)、更新样本分布权重(2)融合多次训练的弱分类器(叠加,按照之前计算的分类器系数)
- AdaBoost 特性:一是训练的错误率上界,随着迭代次数的增加,会逐渐下降;二不容易过拟合。 三:用于二分类不用于回归(用于多分类需要改进,例如以打标签的思想)。四:每次使用全部样本,但是权重不同。五:串行计算 六:对离群点、噪声数据的鲁棒性不好。
- AdaBoost的加权分布体现在两点:对样本加权,误分类样本权重更高、对基学习器加权,性能越好的权重更大。
- AdaBoost 也可以等价为 以指数函数为损失函数的加法模型(即基分类器加权线性叠加)f(x)=∑m=1Mβmb(x;γm),并用前向分布算法来最小化损失函数 minβ,γ∑Ni=1L(yi,βb(ii;γ))。
提升树Boosting Tree:
其基函数为决策树,对分类问题相当于限定基本分类器为分类树,我们使用指数损失函数,此时正是AdaBoost算法的特殊情况,即相当于将AdaBoost算法中的基分类器使用分类树即可。
对回归则是每个模型(回归树)去拟合前者的残差。
损失函数:
(1)回归问题:使用平方误差损失 L(Y,f(X))=(Y–f(X))2
(2)分类问题:使用指数损失函数 L(Y,f(X))=exp(−Yf(X))
梯度提升 gradient boosting:
对于梯度提升树其学习流程与提升树类似只是不再使用残差作为新的训练数据而是使用损失函数的梯度作为新的新的训练数据的y值,具体的来说就是使用损失函数对f(x)求梯度然后带入fm-1(x)计算:
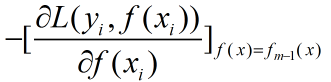
GDBT与提升树之间的关系:
提升树模型每一次的提升都是靠上次的预测结果与训练数据的label值差值作为新的训练数据进行重新训练,GDBT则是将残差计算替换成了损失函数的梯度方向,将上一次的预测结果带入梯度中求出本轮的训练数据,这两种模型就是在生成新的训练数据时采用了不同的方法,那么在这个背后有啥区别?使用残差有啥不好?
李航老师《统计学习方法》中提到了在使用平方误差损失函数和指数损失函数时,提升树的残差求解比较简单,但是在使用一般的损失误差函数时,残差求解起来不是那么容易,所以就是用损失函数的负梯度在当前模型的值作为回归问题中的残差(均方误差)或者残差的近似值