

int uniquePaths(int m, int n){
int i,j;
int dp[m][n];
memset(dp,0,sizeof(dp));
for(i=0;i<m;i++)
{
for(j=0;j<n;j++)
{
if(i==0&&j>0)//边界条件
{
dp[i][j]=dp[i][j-1];
}
else if(i>0&&j==0)//边界条件
{
dp[i][j]=dp[i-1][j];
}
else if(i==0&&j==0)
{
dp[i][j]=1; //边界条件
}
else{
dp[i][j]=dp[i-1][j]+dp[i][j-1]; //状态方程
}
}
}
return dp[m-1][n-1];
}
这一题算是自己第一次看懂点了动态规划的方法,写一些自己的见解,如有错误还请指正。
动态规划问题:
1、确定状态转移方程
首先需要确定状态方程由题可知,用一个二维数组dp[i][j]表示走到(i,j)点的路径个数。由体可知,其结果是dp[i-1][j]和dp[i][j-1]的和。即:dp[i][j]=dp[i-1][j]+dp[i][j-1];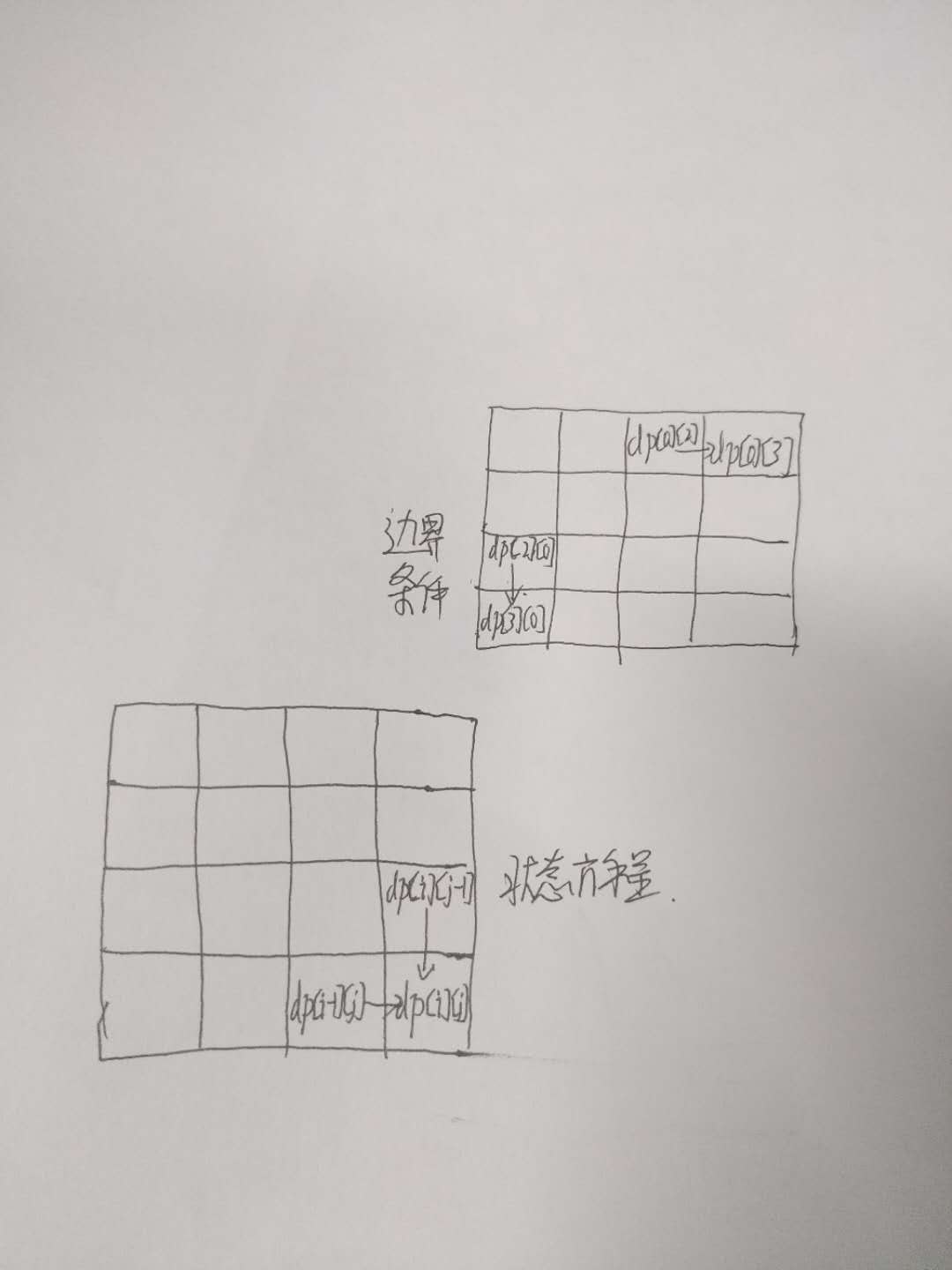
2、确定边界条件
从题中可知,dp[0][0]=1,即从第一个点出发到第一个点有1条路径。对于第一行的元素,由于路径行走只能向右或向下,因此dp[0][j]=dp[0][j-1]=1.同样的对于第一列的元素。dp[i][0]=dp[i-1][0]=1。
大佬的思路。
