Educational Codeforces Round 37
E. Connected Components?
题意:给出的是补图,求原图连通块个数及每个连通块的大小。
tags:原题。。
1】每次选取一个未分配的点,从这个点 bfs。但因为原图太大,我们只能在补图的基础上对原图 bfs。
假设当前点是 u ,如果补图上有边 u -> v ,就把点 v 标记。之后在所有未分配的点中,找没有被标记的点,加入连通块。 注意还要把点 v 的标记取消,因为之后可能还有点会搜到 v 。
2】因为每次要在未分配的点中跑一遍,所以我们要加个链表优化。已经分配的点就从链表中删除。
因为每个点和每条边都只会走一次,复杂度是 O(n+m) 。

// Edu 37 E #include<bits/stdc++.h> using namespace std; #pragma comment(linker, "/STACK:102400000,102400000") #define rep(i,a,b) for (int i=a; i<=b; ++i) #define per(i,b,a) for (int i=b; i>=a; --i) #define mes(a,b) memset(a,b,sizeof(a)) #define INF 0x3f3f3f3f #define MP make_pair #define PB push_back #define fi first #define se second typedef long long ll; const int N = 200005; int n, m, pre[N], nex[N], cnt, ans[N]; bool vis1[N], mark[N]; queue< int > q; vector< int > G[N]; void Delete(int u) { nex[pre[u]] = nex[u]; pre[nex[u]] = pre[u]; ++ans[cnt], mark[u]=true; } void bfs(int u) { ++cnt; q.push(u); Delete(u); while(!q.empty()) { u = q.front(); q.pop(); for(auto to : G[u]) if(!mark[to]) vis1[to]=true; for(int i=nex[0]; i; i=nex[i]) if(!vis1[i]) q.push(i), Delete(i); for(auto to : G[u]) if(!mark[to]) vis1[to]=false; } } int main() { scanf("%d%d", &n, &m); rep(i,1,n) pre[i]=i-1, nex[i]=i+1; pre[1]=0, nex[n]=0, nex[0]=1; int u, v; rep(i,1,m) { scanf("%d%d", &u, &v); G[u].PB(v); G[v].PB(u); } u = 0; while(nex[u]) { mark[nex[u]] = true; bfs(nex[u]); u = 0; } sort(ans+1, ans+1+cnt); printf("%d ", cnt); rep(i,1,cnt) printf("%d ", ans[i]); return 0; }
F. SUM and REPLACE
题意:定义 D(n) 为正整数 n 的正因子个数。两种操作:
- REPLACE l r — for every
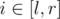 replace ai with D(ai);
replace ai with D(ai); - SUM l r — calculate
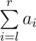 .
.
tags:一眼线段树,区间更新,区间求和。。一开始想 lazy 标记写,结果发现每次必须更新下去,lazy 没有用。。
其实就是一个老套路,D(n) 下降速度很快,如果 n<=2 ,D(n) = n 。所以我们只要记录一下区间最大值,如果 max <= 2 ,就跳出。

// Edu37 F #include<bits/stdc++.h> using namespace std; #pragma comment(linker, "/STACK:102400000,102400000") #define rep(i,a,b) for (int i=a; i<=b; ++i) #define per(i,b,a) for (int i=b; i>=a; --i) #define mes(a,b) memset(a,b,sizeof(a)) #define INF 0x3f3f3f3f #define MP make_pair #define PB push_back #define fi first #define se second #define mid (L+R>>1) typedef long long ll; const int N = 1000005, M = 300005; int n, m, cnt[N]; ll sum[N<<2], mx[N<<2]; void pushup(int ro) { sum[ro] = sum[ro<<1]+sum[ro<<1|1]; mx[ro] = max(mx[ro<<1], mx[ro<<1|1]); } void build(int ro, int L, int R) { if(L==R) { scanf("%lld", &mx[ro]); sum[ro]=mx[ro]; return ; } build(ro<<1, L, mid); build(ro<<1|1, mid+1, R); pushup(ro); } void update(int ro, int L, int R, int l, int r) { if(mx[ro]<=2) return ; if(l<=L && R<=r && L==R) { sum[ro]=mx[ro]=cnt[sum[ro]]; return ; } if(l<=mid) update(ro<<1, L, mid, l, r); if(mid<r) update(ro<<1|1, mid+1, R, l, r); pushup(ro); } ll query(int ro, int L, int R, int l, int r) { if(l<=L && R<=r) return sum[ro]; ll ans = 0; if(l<=mid) ans += query(ro<<1, L, mid, l, r); if(mid<r) ans += query(ro<<1|1, mid+1, R, l, r); return ans; } int main() { rep(i,1,N-1) for(int j=i; j<N; j+=i) ++cnt[j]; scanf("%d%d", &n, &m); build(1, 1, n); int t, l, r; while(m--) { scanf("%d%d%d", &t, &l, &r); if(t==1) update(1, 1, n, l, r); else printf("%lld ", query(1, 1, n, l, r)); } return 0; }
