一、动态规划
动态规划,无非就是利用历史记录,来避免我们的重复计算。而这些历史记录,我们得需要一些变量来保存,一般是用一维数组或者二维数组来保存。下面我们先来讲下做动态规划题很重要的三个步骤,
如果你听不懂,也没关系,下面会有很多例题讲解,估计你就懂了。之所以不配合例题来讲这些步骤,也是为了怕你们脑袋乱了
第一步骤:定义数组元素的含义,上面说了,我们会用一个数组,来保存历史数组,假设用一维数组 dp[] 吧。这个时候有一个非常非常重要的点,就是规定你这个数组元素的含义,例如你的 dp[i] 是代表什么意思?
第二步骤:找出数组元素之间的关系式,我觉得动态规划,还是有一点类似于我们高中学习时的归纳法的,当我们要计算 dp[n] 时,是可以利用 dp[n-1],dp[n-2].....dp[1],来推出 dp[n] 的,也就是可以利用历史数据来推出新的元素值,所以我们要找出数组元素之间的关系式,例如 dp[n] = dp[n-1] + dp[n-2],这个就是他们的关系式了。而这一步,也是最难的一步,后面我会讲几种类型的题来说。
学过动态规划的可能都经常听到最优子结构,把大的问题拆分成小的问题,说时候,最开始的时候,我是对最优子结构一梦懵逼的。估计你们也听多了,所以这一次,我将换一种形式来讲,不再是各种子问题,各种最优子结构。所以大佬可别喷我再乱讲,因为我说了,这是我自己平时做题的套路。
第三步骤:找出初始值。学过数学归纳法的都知道,虽然我们知道了数组元素之间的关系式,例如 dp[n] = dp[n-1] + dp[n-2],我们可以通过 dp[n-1] 和 dp[n-2] 来计算 dp[n],但是,我们得知道初始值啊,例如一直推下去的话,会由 dp[3] = dp[2] + dp[1]。而 dp[2] 和 dp[1] 是不能再分解的了,所以我们必须要能够直接获得 dp[2] 和 dp[1] 的值
案例一、简单的一维 DP
问题描述:一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
(1)、定义数组元素的含义
按我上面的步骤说的,首先我们来定义 dp[i] 的含义,我们的问题是要求青蛙跳上 n 级的台阶总共由多少种跳法,那我们就定义 dp[i] 的含义为:跳上一个 i 级的台阶总共有 dp[i] 种跳法。这样,如果我们能够算出 dp[n],不就是我们要求的答案吗?所以第一步定义完成。
(2)、找出数组元素间的关系式
我们的目的是要求 dp[n],动态规划的题,如你们经常听说的那样,就是把一个规模比较大的问题分成几个规模比较小的问题,然后由小的问题推导出大的问题。也就是说,dp[n] 的规模为 n,比它规模小的是 n-1, n-2, n-3.... 也就是说,dp[n] 一定会和 dp[n-1], dp[n-2]....存在某种关系的。我们要找出他们的关系。
那么问题来了,怎么找?
这个怎么找,是最核心最难的一个,我们必须回到问题本身来了,来寻找他们的关系式,dp[n] 究竟会等于什么呢?
对于这道题,由于情况可以选择跳一级,也可以选择跳两级,所以青蛙到达第 n 级的台阶有两种方式
一种是从第 n-1 级跳上来
一种是从第 n-2 级跳上来
由于我们是要算所有可能的跳法的,所以有 dp[n] = dp[n-1] + dp[n-2]。
(3)、找出初始条件
当 n = 1 时,dp[1] = dp[0] + dp[-1],而我们是数组是不允许下标为负数的,所以对于 dp[1],我们必须要直接给出它的数值,相当于初始值,显然,dp[1] = 1。一样,dp[0] = 0.(因为 0 个台阶,那肯定是 0 种跳法了)。于是得出初始值:
dp[0] = 0. dp[1] = 1. 即 n <= 1 时,dp[n] = n.
三个步骤都做出来了,那么我们就来写代码吧,代码会详细注释滴。
int f( int n ){
if(n <= 1)
return n;
// 先创建一个数组来保存历史数据
int[] dp = new int[n+1];
// 给出初始值
dp[0] = 0;
dp[1] = 1;
// 通过关系式来计算出 dp[n]
for(int i = 2; i <= n; i++){
dp[i] = dp[i-1] + dp[-2];
}
// 把最终结果返回
return dp[n];
}
(4)、再说初始化
大家先想以下,你觉得,上面的代码有没有问题?
答是有问题的,还是错的,错在对初始值的寻找不够严谨,这也是我故意这样弄的,意在告诉你们,关于初始值的严谨性。例如对于上面的题,当 n = 2 时,dp[2] = dp[1] + dp[0] = 1。这显然是错误的,你可以模拟一下,应该是 dp[2] = 2。
也就是说,在寻找初始值的时候,一定要注意不要找漏了,dp[2] 也算是一个初始值,不能通过公式计算得出。有人可能会说,我想不到怎么办?这个很好办,多做几道题就可以了。
下面我再列举三道不同的例题,并且,再在未来的文章中,我也会持续按照这个步骤,给大家找几道有难度且类型不同的题。下面这几道例题,不会讲的特性详细哈。实际上 ,上面的一维数组是可以把空间优化成更小的,不过我们现在先不讲优化的事,下面的题也是,不讲优化版本。
二、状态压缩
状态压缩动态规划,就是我们俗称的状压DP,是利用计算机二进制的性质来描述状态的一种DP方式
在求解背包问题时,我们的状态通常定义为n件物品分别放与不放。 最容易想到的是开个n维数组,但是这样控件浪费且难以实现,我们仔细观察就会发现,每件物品有放与不放两种选择;假设我们有5件物品的时候,用1和0代表放和不放。 如果这5件物品都不放的话,那就是00000; 如果这5件物品都放的话,那就是11111;看到这,我们知道可以用二进制表示所有物品的放与不放的情况;如果这些二进制用十进制表示的话就只有一个维度了。而且这一个维度能表示所有物品放与不放的情况;
这个过程就叫做状态压缩;在状态难以表示并且只有决策情况的时候可以用状态压缩。状压其实是一种很暴力的算法,因为他需要遍历每个状态,所以将会出现2^n的情况数量 ,但是求解的规模n一般不会很大。有了状态,我们就需要对状态进行操作或访问
可是问题来了:我们没法对一个十进制下的信息访问其内部存储的二进制信息,怎么办呢?别忘了,操作系统是二进制的,编译器中同样存在一种运算符:位运算 能帮你解决这个问题。
.判断一个数字x二进制下第i位是不是等于1。
方法:if(((1<<(i−1))&x)>0)if(((1<<(i−1))&x)>0)
将1左移i-1位,相当于制造了一个只有第i位上是1,其他位上都是0的二进制数。然后与x做与运算,如果结果>0,说明x第i位上是1,反之则是0。
2.将一个数字x二进制下第i位更改成1。
方法:x=x|(1<<(i−1))x=x|(1<<(i−1))
证明方法与1类似,此处不再重复证明。
3.把一个数字二进制下最靠右的第一个1去掉。
方法:x=x&(x−1)

UVA1099

题目:给定x*y大小的巧克力,要求只能横着切和纵着切,而且必须一次切到底,即每次切割能把一块巧克力切成两块矩形巧克力 ,问是否能经过若干次操作,把巧克力切成n块,每块面积分别为a1,a2……an;
思路:每次切一刀(可以横着或者竖着)可以把一切巧克力切成两块小的矩形巧克力,我们可以定义状态:dp[x] [y] [s]为给定长宽为xy的巧克力,能否切出面积集合s。用2进制来表示面积集合,假设切为4块,每块为6,3,2,1,则用1111表示该集合,集合从1-1111一共 2的n+1次方-1,为15个集合。因为s的总面积总是和x*y相等的,不同的话肯定切不了,可以用sum[s]保存每个集合的面积,则y=sum[s]/x,可以规定x为巧克力较短的边,可以把状态dp[x] [y] [s]改为dp[x] [s]。
题目要求dp[x] [s],我们可以跟x平行切
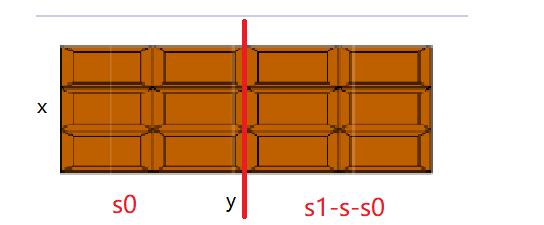
把巧克力切成两块,只要切成的两小块,可以满足切成子集,那么整个大块就也能切,则状态转移为求dp[min(x,sum[s0]/x)] [s0]&&dp[min(x,sum[s1]/x)] [s1]
同时也可以把最短边x切断,
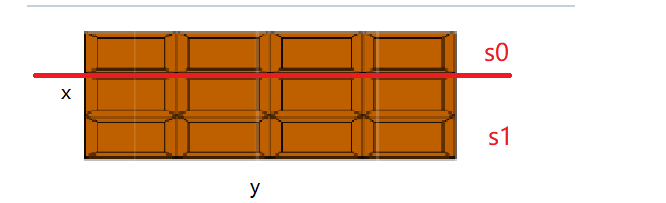
此时状态转移为dp[min(y,sum[s0]/y)] [s0]&&dp[min(y,sum[s1]/y)] [s1]
只要两种切法满足其中一个就可以。转移方程找到了题目就很容易了。
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <stdio.h>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
using namespace std;
const int MAXN = 16;
int n, x, y;
int a[MAXN];
int sum[1 << MAXN];
int dp[101][1 << MAXN]; // 1 为可以 0为不可以 -1为未确定
//计算集合中有几个元素
int bitcount(int a)
{
int rt = 0;
while (a)
{
//依次取最后一位&1,算是否有元素
if (a & 1) rt++;
a >>= 1;
}
return rt;
}
//求短边x下能否切出集合S
int dfs(int x, int s)
{
if (dp[x][s] != -1)return dp[x][s]; //若dp中已经计算过,则直接返回结果
if (bitcount(s) == 1)return dp[x][s] = 1; //集合中只有一个元素,则不需要再切
int y = sum[s] / x; //计算另一边
for (int s0 = (s - 1) & s; s0; s0 = (s0 - 1) & s) //分别给切成的两块不同的集合
{
int s1 = s ^ s0;
if (sum[s0] % x == 0 && dfs(min(x, sum[s0] / x), s0) && dfs(min(x, sum[s1] / x), s1))
return dp[x][s] = 1;
if (sum[s0] % y == 0 && dfs(min(y, sum[s0] / y), s0) && dfs(min(y, sum[s1] / y), s1))
return dp[x][s] = 1;
}
return dp[x][s] = 0;
}
int main()
{
int cs = 1;
while (scanf("%d", &n) != EOF)
{
if (n == 0)break;
scanf("%d%d", &x, &y);
int ct = 0;
for (int i = 0; i < n; i++)
{
scanf("%d", &a[i]);
ct += a[i];
}
if (ct != x * y || ct % x != 0)
{
printf("Case %d: No
", cs++); continue;
}
//all表示原始的集合
//如果n=3 1<<3-1=111
//如果n=4 1<<4-1=1111
int ALL = (1 << n) - 1;
//计算每个集合的面积
// 1236
//1 2 3 6 =>1111 sum[15]=12
//1 =>1000 sum[8]=1
//23 =>0110 sum[6]=6
for (int s = 0; s <= ALL; s++)
{
sum[s] = 0;
for (int i = 0; i < n; i++)
{
if (s & (1 << i))
{
sum[s] += a[i];
}
}
}
memset(dp, -1, sizeof dp);
if (dfs(min(x, y), ALL) == 1)
{
printf("Case %d: Yes
", cs++);
}
else {
printf("Case %d: No
", cs++);
}
}
return 0;
}