编译原理之语法分析-自下而上分析(一)

　　从名字很容易看出来，自下而上分析法对应的就是自上而下分析法，这里我首先简单区分一下这两种分析方法的区别。

　　自上而下分析法是多个推导的过程，而自下而上分析法是多个归约的过程。那么归约和推导又是什么呢？下面通过一个简单的例子说明。

　　　　例如有一个文法G（S） :  ①S -> aAcB ，②B->b，假如有一个输入符号串为aAcb。说明：G(S)中的S说明S是开始符号。

　　　　推导(从开始符号开始):第一步：S->aAcB，第二步：B->b。

　　　　经过两步之后我们就能推到出输入符号串aAcb。而第一步中我们从S推出aAcB的过程就是推到的过程，同理第二步中B推出b也是推到的过程。

　　　　归约(从输入符号串开始):第一步：aAcb中的b归约为B，第二步：aAcB归约为S。

　　　　经过两步之后我们将输入符号串aAcb中的b根据②中的规则替换(归约)为B,这时输入符号串从aAcb变为aAcB，然后再根据规则①将aAcB归约为S。

　　　　通过这个例子我们可以总结一句话：推导的过程就是从某个产生式的左部(S)推导出右部(aAcb)的过程。归约的过程是从某个产生式的右部(aAcb)归约(替换)为左部(S)的过程。

　　　　多个推导的过程能够组成自上而下分析即从开始符号到输入符号串的过程，多个归约的过程能够组成自下而上分析即从输入符号串到开始符号的过程。

　　(一)什么是自下而上分析法

　　　　自下而上分析法定义：从输入串开始，逐步进行归约，直至文法的开始符号。

　　　　在自下而上分析法中使用的方法(移进-归约法)：使用一个符号栈，把输入符号逐一移进栈，当栈顶形成某个产生式右部时，则将栈顶的这一部分替换(归约)成该产生式的左部符号。(下图就是一个移进-归约的例子)。

1. 1. 符号栈方式展示移-进归约法
      

　　　　

 　　　　从图中可以发现移进-归约法就是将输入符号串(从左到右)依次读入，每读入一个字符就和所有产生式的右部对比，查看是否能归约为产生式左部。(即图中符号栈最后三个状态)，读入b时和产生式②对比可归约为B，此时符号栈变为aAcB，又和产生式①对比可归约为S。

　　　　　　2.分析树方式展示移-进归约法

　　　　　　　　

　　　　从分析树中，从根节点到叶子节点就是自上而下分析法，从叶子节点逆推到根节点就是自下而上分析法。

　　　  （二）自下而上分析法之短语、直接短语、句柄

　　　　上边我们简单了解了一下什么时自上而下分析法，下边我们在说明如何进行归约前先搞清楚几个定义(短语、直接短语、句柄)。 直接上图给出这三个比较标准的定义。

 　　　　

 　　　 下边通过分析树中的文法对这三个定义进行分析（以下为个人见解）。

　　　  给出文法(如下图)求句型aAbcde的短语、直接短语、句柄。(画出从S推导出aAbcde的分析树)

           

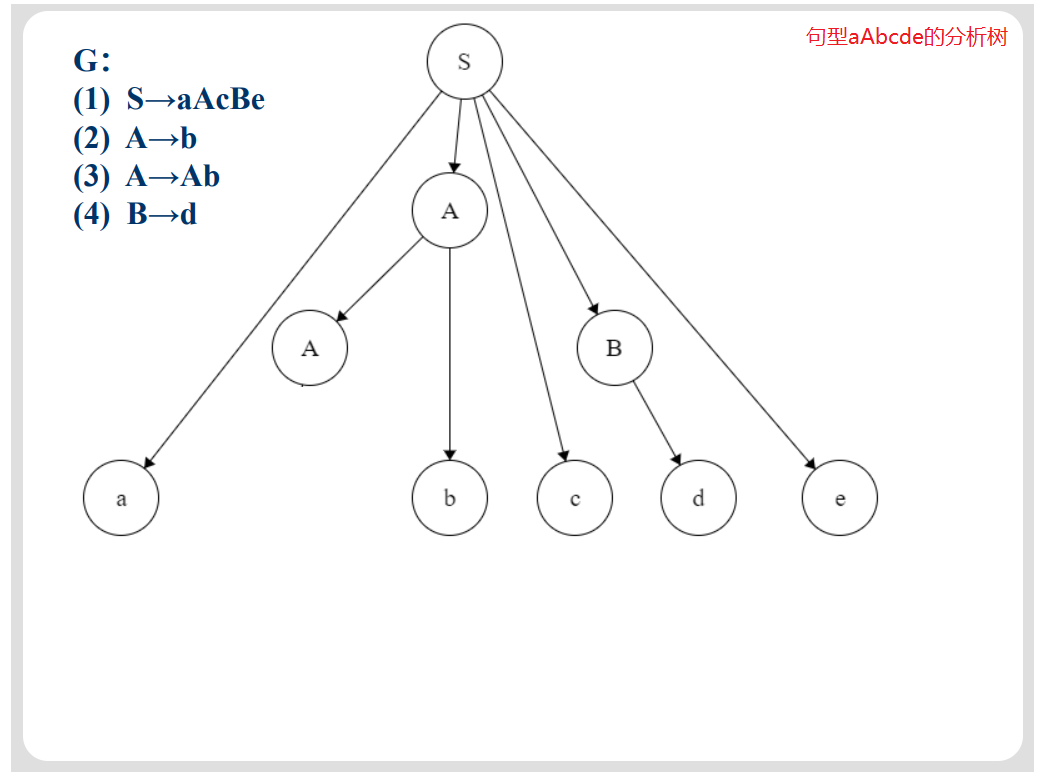
　　　  短语：在分析树中，所有父节点的最终叶子节点组成的集合。

　　　　　　  例如：根节点S，它直接指向的节点为aAcBe,但是A和B还有子节点，因此A和B就不是根节点S的最终叶子节点。应该将A->Ab，然后B->d。最终得出aAbcde是关于S的短语。

　　　　　　　　　  父节点A，它直接指向的节点为Ab,而A和b均为叶子节点，因此Ab就是关于A的短语。

　　　　　　　　　  父节点B，它直接指向的节点为d，而d为叶子节点，因此d是关于B的短语。

　　　  直接短语：只需要一步转换的短语称为直接短语。

　　　　　　  例如：父节点 A，A->Ab可一步推导出，因此Ab属于直接短语。

　　　　　　　　　  父节点B，B->d可一步推导出，因此d属于直接短语。

　　　　　　　　　  根节点S，因为S->aAbcde不能一步推导出来，还需要将A->Ab,B->b,因此aAbcde就不属于直接短语。

　　　  句柄：分析树中最左侧的直接短语。如上图中直接短语Ab位于最左侧，而直接短语d在Ab的右边，所以Ab是句柄。

　　　  注意：具有二义性文法的句柄可能不唯一。例如：文法G(E):  E-> E+E | E*E | (E) | i ,给出句型E+E*E的句柄。

　　　　(1)E -> E+E -> E+E*E> 句柄为E*E

　　　　(2)E -> E*E -> E+E*E  句柄为E+E

　　　 （三）规范归约

　　　　规范归约定义：将句柄替换成相应产生式左部符号而得到的，则该序列是一个规范归约。最左归约的过程就是不断将句柄转换成产生式左部(每归约一次句型的句柄就变化一次)。

　　　　

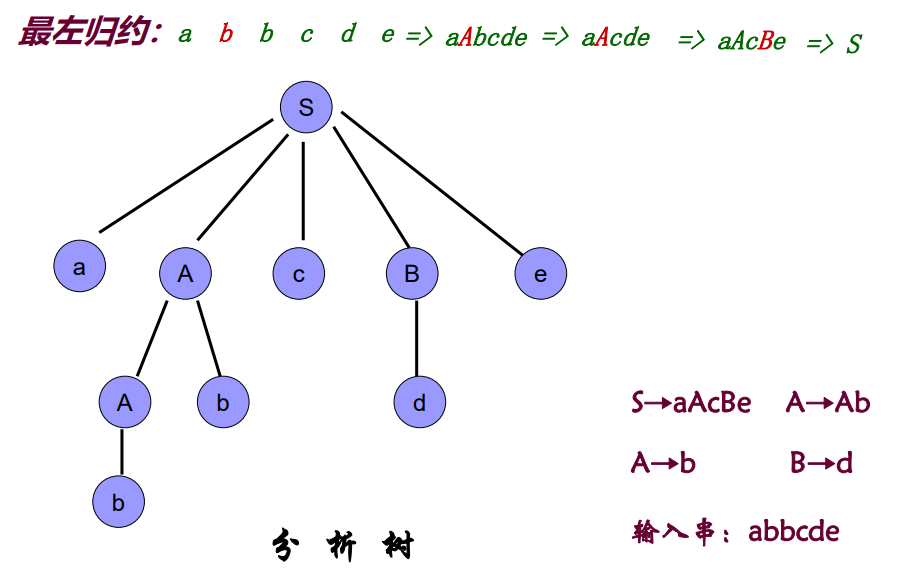
 　　　　例如上图中规范规约的过程：

　　　　①句柄为b，根据A->b,将句柄b(左侧的b)归约为A，此时句柄变为Ab。

　　　　②句柄为Ab，根据A->Ab,将句柄Ab归约为A，此时句柄为d。

　　　　③句柄为d，根据B->d，将句柄d归约为B，此时句柄为aAcBe。

　　　　④句柄为aAcBe，根据S->aAcBe，将句柄aAcBe归约为S，最左推导过程结束。
　　　　其实最左推导的过程就是“剪枝"的过程，①将b节点剪去，②将Ab节点剪去，③将d节点剪去，④将aAcBe剪去，最终只剩下S节点。

　　　　规范归约的基本问题：

　　　　1、如何找出或确定可归约串——句柄？

　　　　2、对找出的可归约串——句柄替换为哪一非终结符号？

　　　　基于上述两个问题，实现移进-归约分析的一个方便途径是用一个栈和一个输入缓冲区，用#表示栈底和输入的结束。

　　　　

　　　　对于栈和输入缓冲区的使用可尝试推导下图中的例子，由于例子较为复杂，篇幅有限这里不做详细详解。

　　　　

 　　　　

　　　　对于语法分析的操作(即上图中的动作)共有四种状态：

　　　　1、移进：下一输入符号移进栈顶，指针（读头）后移。

　　　　2、归约：检查栈顶若干符号能否进行归约，若能，就以产生式左部代替该符号串，同时输出产生式编号。

　　　　3、接受：移进-归约的结局是站内只剩下栈底符号和文法开始符号，(指针)读头也指向语句的结束符。

　　　　4、出错：发现了一个语法错误，调出出错处理程序。(可归约串一定处于栈顶位置，而不可能出现在栈顶的下方，因为一旦出现可归约串就会及时将其归约掉，不会出现栈顶有归约串而继续读入符号的情况)。

 　　　 

　　　　 以上均为个人学习总结，如有错误或异议欢迎提出（自下而上分析法未完待续......）。