Problem Description
 Background
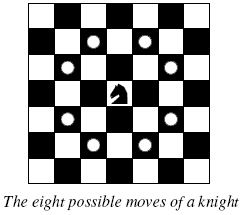
Background The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?
Problem
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.
Input
The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .
Output
The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number.
If no such path exist, you should output impossible on a single line.
If no such path exist, you should output impossible on a single line.
Sample Input
3
1 1
2 3
4 3
Sample Output
Scenario #1:
A1
Scenario #2:
impossible
Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4
**************************************************************************************************************************
深搜dfs(),经典体现,
***************************************************************************************************************************

1 #include<iostream> 2 #include<string> 3 #include<cstring> 4 #include<cstdio> 5 #include<algorithm> 6 #include<cmath> 7 using namespace std; 8 int d[8][2]={-2, -1, -2, 1, -1, -2, -1, 2, 1, -2, 1, 2, 2, -1, 2, 1}; 9 int s[29][29]; 10 char p[100]; 11 int m,n,cas; 12 int dfs(int x,int y,int mark) 13 { 14 if(mark==n*m) return 1; 15 for(int i=0;i<8;i++) 16 { 17 int dx=x+d[i][0]; 18 int dy=y+d[i][1]; 19 if(dx<m&&dx>=0&&dy<n&&dy>=0&&s[dy][dx]==0) 20 { 21 s[dy][dx]=1; 22 p[(mark<<1)]='A'+dx; 23 p[(mark<<1)+1]='1'+dy; 24 if(dfs(dx,dy,mark+1))//dfs精华 25 return 1; 26 s[dy][dx]=0; 27 } 28 } 29 return 0; 30 } 31 int main() 32 { 33 scanf("%d",&cas); 34 int k; 35 for(k=1;k<=cas;k++) 36 { 37 scanf("%d%d",&n,&m); 38 memset(s,0,sizeof(s)); 39 memset(p,0,sizeof(p)); 40 s[0][0]=1; 41 p[0]='A'; 42 p[1]='1'; 43 if(dfs(0,0,1)) 44 { 45 printf("Scenario #%d: ",k); 46 for(int it=0;it<strlen(p);it++) 47 printf("%c",p[it]); 48 printf(" "); 49 50 } 51 else 52 { 53 printf("Scenario #%d: impossible ",k); 54 } 55 56 } 57 }
