P值就是当原假设为真时,比所得到的样本观察结果更极端的结果出现的概率。
以下延续白话系列,解释一下,“什么是P值,什么是极端”,算是郑文的一个长长的注脚。
回到上次的硬币试验,那是一次二项试验,每次试验投100次,记下出现正面的次数,比如,如果
每次出现的正面数都是50,你就有把握认为这是一枚均匀的硬币;
正面数等于45或者等于55,你就有一点点的怀疑它是均匀的;
正面数等于30或者等于70,比较怀疑;
正面数等于10或者等于90,非常怀疑。
如上,正面数和反面数的差异越大,你就越有把握认为硬币不是均匀的(拒绝原假设)。重复一下P值的定义,“P值就是当原假设为真时,比所得到的样本观察结果更极端的结果出现的概率”,把这个定义套入上述硬币试验的场景中,比如你观察到“正面数是10或者90,正反面次数差异是80”:
如果原假设为真(硬币是均匀的),P值就是你投100次,所得的正反面数差异大于80的概率。
如果这个P值很大,表明,每次投100次均匀的硬币,经常有正反面差异大于80的情形出现。如果这个P值很小,表明,每次投100次均匀的硬币,你很难看到正反面的差异会超过80。
以前说过,10-90是A博士的接受区域。如果一枚硬币投出的正反面次数,差异大于80,——这真是一个“极端”的情形,连保守的A博士看了都摇摇头,不能接受原假设,只好认为原假设不对,硬币是有偏的。这里的逻辑是:
在假定原假设为真的情况下,出现所看到的偏差(正反面差异为80),是这么地不可能(P值很小),以至于我们不再继续相信原假设。
参考资料:
1. 维恩堡《数理统计初级教程》(常学将等译,太原:山西人民出版社,1986,Statistics: An Intuitive Approach By George H. Weinberg and John Abraham Schumaker)
2. Statistics I: Course Notes, 2008 SAS Institute Inc. Cary, NC, USA链接:https://www.zhihu.com/question/23149768/answer/23758600
来源:知乎
著作权归作者所有,转载请联系作者获得授权。
P.S. 1 在我的故事里,显著性水平被称为α,“检验的势”被称为“检验力”,power..
P.S. 2 要彻底理解这三个概念,故事真的不够,建议在有了更多了解之后,看这篇文章《Scientific method: Statistical errors : Nature News & Comment》,或者果壳的翻译版《统计学里“P”的故事:蚊子、皇帝的新衣和不育的风流才子》
故事1
公司A全国的某个岗位X有1000人应聘,这1000人当中,有400是真的符合公司要求的,有600个是能力不达标来碰运气的。这间公司对自己的测试题很有信心(觉得只有5%的人能碰运气通过),没有面试,只是让所有应聘者参加这个测试,只要测试通过就录取入职,根据一年后的表现决定留任、升职还是裁员。最后350人通过测试,入职
但是实际上呢,其实5%浑水摸鱼的人因为种种原因通过了测试,20%真正有能力的人又因为其他种种原因没有通过测试
这些人工作一年后,根据他们的表现,公司发现,其中320人是真的符合公司要求的,30人是碰运气给碰进来的。也就是如下图的情况
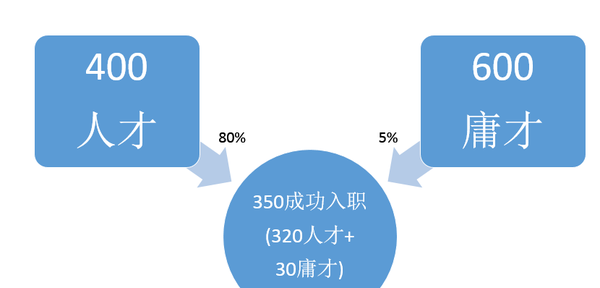
有30个(8.57%>5%)浑水摸鱼的,看来这测试不太行啊..
故事2
公司B全国的某个岗位Y有1000人应聘,这1000人当中,有800是真的符合公司要求的,有200个是能力不达标来碰运气的。这间公司也对自己的测试题很有信心(觉得只有5%的人能碰运气通过),没有面试,只是让所有应聘者参加测试,只要测试通过就录取入职,根据一年后的表现决定留任、升职还是裁员。最后650人通过测试,入职
但是实际上呢,其实5%浑水摸鱼的人因为种种原因通过了测试,20%真正有能力的人又因为其他种种原因没有通过测试
这些人工作一年后,根据他们的表现,公司发现,其中640人是真的符合公司要求的,10人是碰运气给碰进来的,也就是如下图的情况
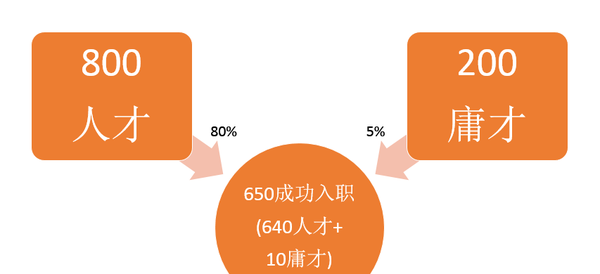
650人里只有10人(1.54%<5%)是浑水摸鱼的,这个测试还不错~
为什么要说这两个坑爹的故事?(哪有公司这么招人的= =)因为这和研究者在进行“通过样本推断总体”一类的研究时的情况类似,不过两家公司代表的可能是不同的研究领域。而用故事最后的比例对比5%来判断故事中的测试是否“有用”,是很容易犯的一个错误
所谓显著性水平α,就是你允许最多有多大比例庸才(H0)通过你的测试——你允许最多有多大比例“H0”被你误以为是H1。这是预先设置好的,在研究前就存在的。为了防止浑水摸鱼的人靠运气入职公司,你的测验不能太简单
所谓检验力power,就是你的测试能够让多大比例人才(H1)通过——你有多大能力发现"H1是H1"。检验力分两种,一种是事前检验力,即在正式进行研究前,你预先设定一个检验力标准,为了获得这么大的检验力(以防人才没有被你招进来),你需要对研究进行一些设计(公司需要设计一份“好”的测试,例如不要太难);另一种是回溯性检验力,即在研究进行之后,根据结果计算自己在研究中实际拥有的检验力。故事里的两个其实都是回溯性检验力
如何权衡上面两者,就看所在领域,及研究者自身了(公司的偏好、决策,以及对于损失人才和浪费资源在庸才两种不同类型的风险承担能力)
而p值,我的理解则是实际上你让庸才之中的多大比例庸才(H0)招了进来,而不是入职者当中的庸才比例。故事里两个p值都是.05,但是入职者当中的庸才比例却不是.05。这是最容易混淆的两点。放到研究里,假设p=.030,意思是说你的研究有3%的可能是在“H0”这个库里面被发现而错误地归入H1;而不是指3%的可能在“包含H0和H1的所有现象”这个库里被发现。后一个比例的大小,相当于故事里入职庸才在所有入职人士中的比例,这个比例取决于在应聘者(你想要检验的假设的总体)当中,有多少是人才(H1),有多少是庸才(H0)
链接:https://www.zhihu.com/question/23149768/answer/23751377
来源:知乎
著作权归作者所有,转载请联系作者获得授权。
前半句话大家理解起来都没问题,重点在理解后半句——出现现状或更差的情况。
举个例子:
假如我有特别的打电话技巧,我告诉楼主接我电话的人都是女生。
楼主不信,于是他要做试验来检验。
他默默的写下原假设和备择假设:
原假设(没有确凿证据一般不推翻的假设):这个人没有特别的打电话技巧,也就是他打电话是男是女接听的概率都是1/2。
备择假设:他真的有特别的打电话技巧。
好了然后我们做实验:我在楼主面前打了20个电话,这20个电话里有18个是娇滴滴的萌妹子回复的。
那这个实验的p值怎么算呢?
在假设原假设(H0)正确时:所以现在我们都假设接我电话的人的性别是随机的,也就是接听我电话的人是男是女的概率分别为1/2。
出现现状或更差的情况:对楼主来说,20个里有18个萌妹子已经是很奇怪的了。如果有19个?甚至20个都是岂不是更奇怪么?所以,出现现状或更差的情况代表着:接我电话的妹子等于或超过18个。
这下p值就清楚了吧:
楼主看了一眼这么多0,觉得还是吹的可能性还是很小的,于是就拒绝了原假设,接受了我“真的有特别的打电话技巧的”备择假设。
可是呢!!!!!!
千万不要以为你这就理解了出现现状或更差的情况哦!
更多时候,我们会遇到这种情况:
我们检验硬币的均匀性:
原假设(没有确凿证据一般不推翻的假设):硬币均匀,正反出现概率各为1/2。
备择假设:硬币不均匀。
如果这次试验我们抛了20次硬币,18次出现正面,出现现状或更差的情况是什么呢?
答案是:出现18次、19次、20次正面和0次、1次、2次正面。(不是出现18、19、20次正面哦!)
我可没说这个硬币正面出现概率多,所以这个时候出现18次正面和出现18次反面(2次正面)或更差的情况(19正、19反、20正和20反)一样是更坏的情况。
这也是为什么当前排名第一的 @李锦霞的答案是错误的原因。他的答案应该是1/1048576*2
当然,如果你以后继续学习概率论的知识的话,有可能碰到比单侧和双侧更难的情况。当然我就不让你犯迷糊了。
最后回到另一个问题:为什么我不对楼主的命题进行分析呢?
因为楼主的命题要求:H0:他是合格的射手(p=1)
这下....只要出现任意一次没射中,p就 小于等于 1-至少全中=1-1*1*1*1*1……=0
看到了吗?一次没中,H0就一定拒绝了。同理,在检验很多东西的时候,你不能说绝对如何如何。
因为数理统计告诉你:小概率发生不正常;而概率论告诉你:一切皆有可能。
很重要的一点是:对于该样本,在假设原假设(H0)正确时,出现现状或更差的情况的概率。
这个例子也很不好,如果真是假设p=1的情况,也根本不能这么用,因为这影响了停止规则。
详见:http://arxiv.org/pdf/1311.0081.pdf
其实 p-value 真的没有你们想象的那么厉害,它会被样本影响,会被停止规则影响,会被很多乱七八糟的事情影响。
其实这个事情理解起来非常简单,我们知道p-value 它是一个随机变量。
那么作为一个随机变量,它是有分布的,那么在原假设的情况下,它的分布是什么呢?
p-value在原假设成立的情况下,它是服从均匀分布(uniform)的。
p-value本身是从type-I error,也就是我们俗称的alpha 来的,而正因为alpha 是服从uniform 的distribution,我们才会说它是在假设原假设(H0)正确时,出现现状或更差的情况的概率。
那如果有停止规则了呢?
这时alpha的distribution 可就变了,例如在原假设p=1的情况中,按照@姚岑卓的说,alpha其实为0,因为在原假设成立的情况下,是不会有type-1 error的,那么也就是没有p-value的说法。
说完停止规则,我们来说说样本的影响,样本的影响更具有现实应用意义。
由于在没有互联网的时候,数据采集很难,我们总是把样本当作样本总体,因为数据本身就很少,迭代也并不快,所以这么做也没有什么关系。但是随着互联网的发展,这么做已经不是很合适了。
举个现实中的例子。
一个互联网网站,要做一个a/b testing,比如说就是检验一个工具的加入会不会增加用户对某个按钮的点击量。那么这个网站在今天收集了5000组用户数据,一组没有新工具,一组有新工具,发现p-value <0.05。
那么这能说明这个工具有效果么?
其实是不行的,原因是在原假设成立的情况下,p-value遵从均匀分布,出现一次p-value<0.05又有什么不可能,你第二天再做一次出现p>0.95都有可能的。
所以experimental design 是怎么做的呢?我们日均有大量的数据,我们不停的做5000个样本的t-test,看p-value是否遵从均匀分布,如果不遵从,我们才可以说这个工具有效果。
这不是我瞎说的哦,Dow Jones就是这么做的。只不过他们为了区别机器人的影响,做了很多假的样本,也就是a/a testing。在原假设成立的情况下(不引入工具的很多个样本相互比较),如果p-value 不服从均匀分布,那这里面就有机器人在作祟。
这就是为什么我要强调p-value要针对样本。在题例中,射飞镖射10000次,你做t-test,p-value<0.05,那是说针对这10000次射飞镖,在假设原假设(H0)正确时,出现现状或更差的情况的概率小于0.05。你只是感觉10000次都这样了,那对于之后的几次应该都小于0.05,但这只是感觉。但你也可以每次射100支,一共做100次,每次都取个p-value,看p-value的distribution,发现并不是uniform的distribution,来说明原假设不成立。前者样本大,但对于总体说明小,后者样本虽小,但对于总体确实更有把握。
不得不提的P值
一、P值的由来
R·A·Fisher(1890-1962)作为一代假设检验理论的创立者,在假设检验中首先提出P值的概念。他认为假设检验是一种程序,研究人员依照这一程序可以对某一总体参数形成一种判断。也就是说,他认为假设检验是数据分析的一种形式,是人们在研究中加入的主观信息。(当时这一观点遭到了Neyman-Pearson的反对,他们认为假设检验是一种方法,决策者在不确定的条件下进行运作,利用这一方法可以在两种可能中作出明确的选择,而同时又要控制错误发生的概率。这两种方法进行长期且痛苦的论战。虽然Fisher的这一观点同样也遭到了现代统计学家的反对,但是他对现代假设检验的发展作出了巨大的贡献。)Fisher的具体做法是:
- 假定某一参数的取值。
- 选择一个检验统计量(例如z 统计量或Z 统计量) ,该统计量的分布在假定的参数取值为真时应该是完全已知的。
- 从研究总体中抽取一个随机样本4计算检验统计量的值5计算概率P值或者说观测的显著水平,即在假设为真时的前提下,检验统计量大于或等于实际观测值的概率。
- 如果P<0.01,说明是较强的判定结果,拒绝假定的参数取值。
- 如果0.01<P值<0.05,说明较弱的判定结果,拒接假定的参数取值。
- 如果P值>0.05,说明结果更倾向于接受假定的参数取值。
可是,那个年代,由于硬件的问题,计算P值并非易事,人们就采用了统计量检验方法,也就是我们最初学的t值和t临界值比较的方法。统计检验法是在检验之前确定显著性水平αα,也就是说事先确定了拒绝域。但是,如果选中相同的αα,所有检验结论的可靠性都一样,无法给出观测数据与原假设之间之间不一致程度的精确度量。只要统计量落在拒绝域,假设的结果都是一样,即结果显著。但实际上,统计量落在拒绝域不同的地方,实际上的显著性有较大的差异。
因此,随着计算机的发展,P值的计算不再是个难题,使得P值变成最常用的统计指标之一。

三、P值的意义
P值就是当原假设为真时所得到的样本观察结果或更极端结果出现的概率。如果P值很小,说明这种情况的发生的概率很小,而如果出现了,根据小概率原理,我们就有理由拒绝原假设,P值越小,我们拒绝原假设的理由越充分。
总之,P值越小,表明结果越显著。但是检验的结果究竟是“显著的”、“中度显著的”还是“高度显著的”需要我们自己根据P值的大小和实际问题来解决。