我们利用势能分析来对splay旋转的复杂度进行简单证明,具体操作暂时不证明
设旋转的复杂度为(k),定义
(size(x):)以x为根的子树大小
(phi(x)=klog_2(size(x)))
(Phi(T)=sum_{phi(x)})
(Phi)为势函数
对于不平衡的树,(Phi)会大,平衡的树(Phi)会小
我们需要计算(DeltaPhi),也就是旋转操作导致的势能变化,需要分情况讨论,用(phi'(x))表示操作完之后的(phi(x))
然后考虑(log)函数的凸性
[egin{aligned}logx_1+logx_2&leq 2logfrac{x_1+x_2}{2}\&leq2log(x_1+x_2)-2\&leq 2log(x_1+x_2+a)-2(ageq 0)end{aligned}
]
于是(logx_1+logx_2-2log(x_1+x_2+a)leq-2(ageq0))
假设(x,p,g)是操作完影响到的点
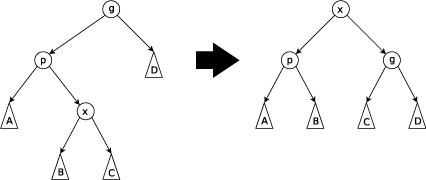
因为zig和zag是一样的,所以我们只考虑zig
对于zig
[egin{aligned}DeltaPhi&=phi'(p)-phi(p)+phi'(x)-phi(x)\&=phi'(p)-phi(x)\&leq phi'(x)-phi(x)end{aligned}
]

对于zig-zig
[egin{aligned}DeltaPhi&=phi'(g)-phi(g)+phi'(x)-phi(x)+phi'(p)-phi(p)\&=phi'(g)+phi'(p)-phi(p)-phi(x)\&leq phi'(x)+phi'(g)-2phi(x)\&leq3phi'(x)-3phi(x)+(phi(x)+phi'(g)-2phi'(x))\&leq3(phi'(x)-phi(x))-2kend{aligned}
]
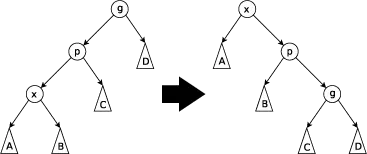
对于zig-zag
[egin{aligned}DeltaPhi&=phi'(g)-phi(g)+phi'(x)-phi(x)+phi'(p)-phi(p)\&=phi'(g)+phi'(p)-phi(p)-phi(x)\&leq phi'(x)+phi'(g)-2phi(x)\&leq2phi'(x)-2phi(x)+(phi'(p)+phi'(g)-2phi'(x))\&leq2(phi'(x)-phi(x))-2kend{aligned}
]
于是我们算出对于双旋
[egin{aligned}D'&=D+DeltaPhi\&leq2k+3k(phi'(x)-phi(x))-2k\&=3k(phi'(x)-phi(x))end{aligned}
]
那么splay到根的均摊代价为(3k(phi(rt)-phi(x))=O(logn)),zig只有一次操作,所以只会使均摊代价增加(k)
于是我们就证得一次splay时间复杂度为(O(logn))