Part 0:前置知识
为了更好地阅读这篇文章,你需要自己百度:
- 树形结构
- 二叉树
- 完全二叉树和满二叉树
- 数组
Part 1:啥是堆
堆是一个完全二叉树,那首先我们来画一个完全二叉树(每个圆圈的数字是他在数组里边的下表):

容易看出堆有一个容易看出的特性(前提是你对树结构的根与叶很敏感,不敏感就记下来):父节点为他的两个子节点的和的二分之一向下取整,也就是:
堆也有分类,一般分为大根堆和小根堆。
我希望你看了这俩图后,你能区分大根堆和小根堆(这个时候圆圈里的数字是数据):
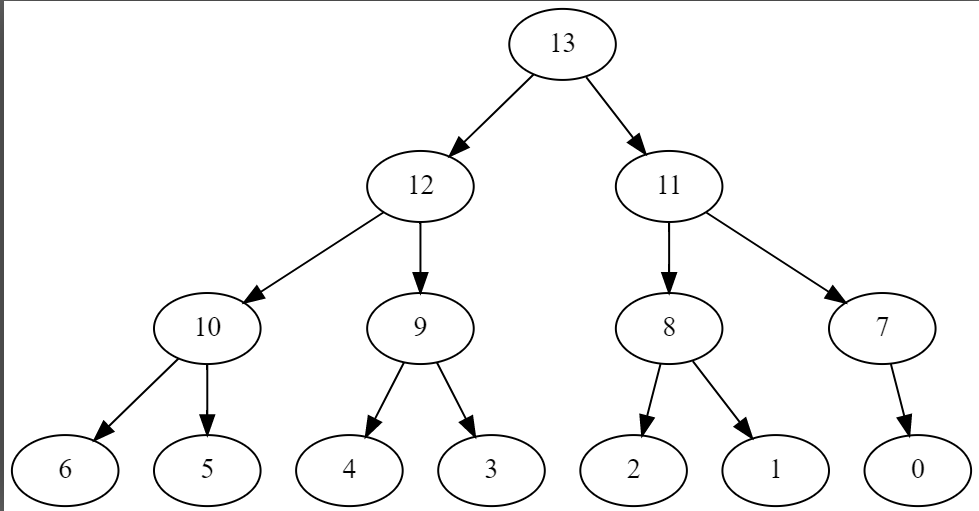
这是大根堆,接下来的是小根堆:
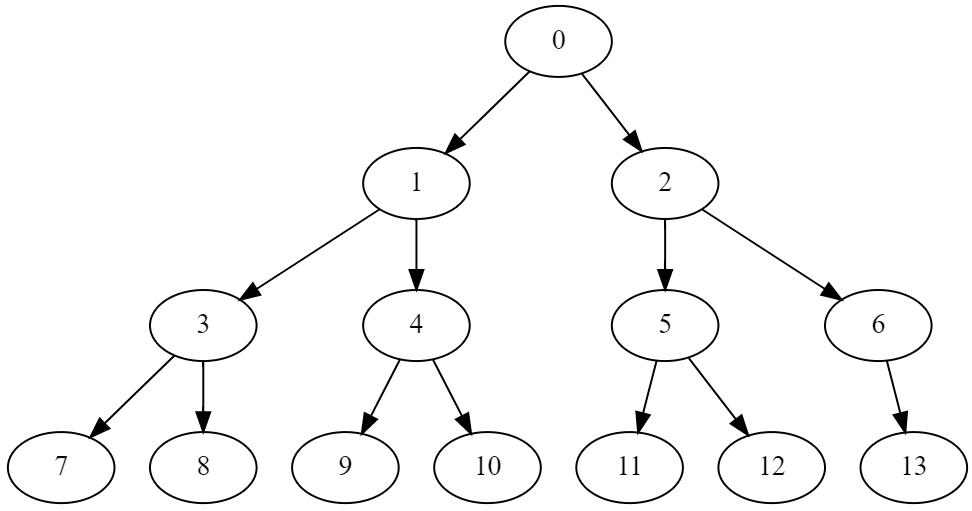
这里笔者给出记忆方法:上大下小大根堆,上小下大小根堆
Part 2:堆的基本操作
堆的基本操作有一下几个:
- 上浮(上调节点) shift_up
- 下沉(下调节点) shift_down
- 插入(插入节点) push
- 弹出(弹出节点)pop
- 取顶(得到最顶端的节点) top
- 堆排序(排序)heap_sort
我们用比较好理解的小根堆来讲一讲前五个操作,第六个堆排序我们单独拿一节来说。
上浮
我希望你记住了小根堆的特性:上小下大。
假设,这个时候我们有这么一个堆:
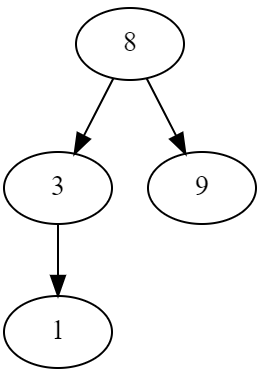
但显然,这个不是个小根堆,我们想要把他变成小根堆,我们需要:
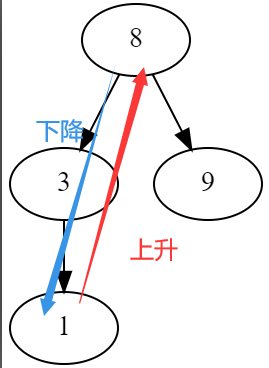
于是他会变成这个样子:
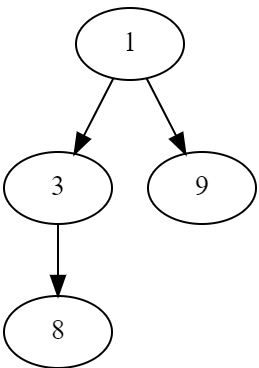
这个操作我们把他成为:上浮。
上浮的操作本质就是swap,一直当前节点与他的父节点的大小,然后选择是否交换。
//这里的heap数组是存放堆的数组
//请注意:不是所有的堆一开始就是小根堆和大根堆
//在进行几次上浮和下沉后,才能保证他是一个大根堆或者小根堆
void Shift_up(int i){
while(i/2 >= 1){ //一直比较到最顶端
if(heap[i] < heap[i/2]){ //int的特性:int/int = floor(double/double)
swap(heap[i],heap[i/2]);
i /= 2; //这个时候相当于指向i的一个指针要向上走,走到他的父节点
}
else break;
}
下沉
上浮固然是个好方法,但有时候不让你用上浮,你也可以用下沉。
还是拿这个图举例子:
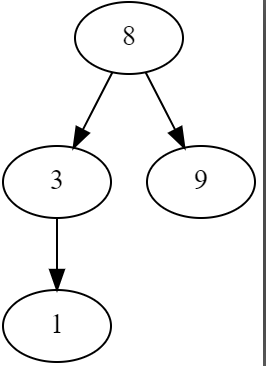
我们可以看到,8要向下下沉,那他该往哪里下沉?3还是9?显然是3。为什么?因为3<9!
那么我们就有这个代码:
void Shift_down(int i ,int n){//n表示当前有n个节点
while(i*2 <= n){
int t = i * 2 ;
if(t+1 <= n && heap[T+1] < heap[T]) T++;
if(heap[i] < heap[T]){
swap(heap[ i ],heap[T] );
i = T;
}
else break;
}
插入
我们把一个元素插入到根的末尾,然后让他上浮就好了:
void Push(x){
n++; //n是表示当前有多少个元素
heap[n] = x;
Shift_up(n);
}
弹出
让根节点元素和尾节点进行交换,然后让现在的根元素下沉就可以了。
void Pop(x){
swap(heap[1],heap[n]);
n--;
Shift_down( 1 );
}
取顶
这个你不会请滚回百度百科吧:
int top(){
return heap[1];
}
堆排序
堆排序真的在排序吗?不是,他的本质是不断的在上浮和下调,每次让最小的一定能跑到最上面,取顶,POP,QED。
void Heap_sort(int arr[]){
k=0;
while(size > 0){
k++;
arr[k] = top();
pop();
}
}
复杂度(O(N log N)),还不错,不过空间的话……
Part 3:优先级队列
优先级队列其实是队列的一个变体,在小学的时候,你也许会做过这么一种题:
有(n)个小朋友排队打饭,他们所需要的时间分别为(n_i),当前一个小朋友打饭的时候,后面的小朋友就要等。怎么排序才能让等待时间之和最短。
(以下是待更新部分)