补充一点性质
[sum_{d|n}varphi(d) = n
]
证明:
对于 (n = 1) ,不难验证满足题意
对于 (n = p^a) ,
[sum_{d|n}varphi(d) = 1 + sum_{i = 1}^avarphi(p^i) \=p^a = n
]
对于 (n = p_1^{a_1}...p_k^{a_k})
[sum_{d|n}varphi(d) = sum_{i=0}^{a_1}varphi(p_1^i)sum_{i=0}^{a_2}varphi(p_2^i)...sum_{i=0}^{a_k}varphi(p_k^i)\=p_1^{a_1}...p_k^{a_k} = n
]
- 若
i % p == 0则 (varphi(i*p) = varphi(i) * p) , (p) 是质数
D. Easy Math
题意:
给定 (m,n) 求
[sum_{i=1}^mmu(i * n)
]
解:
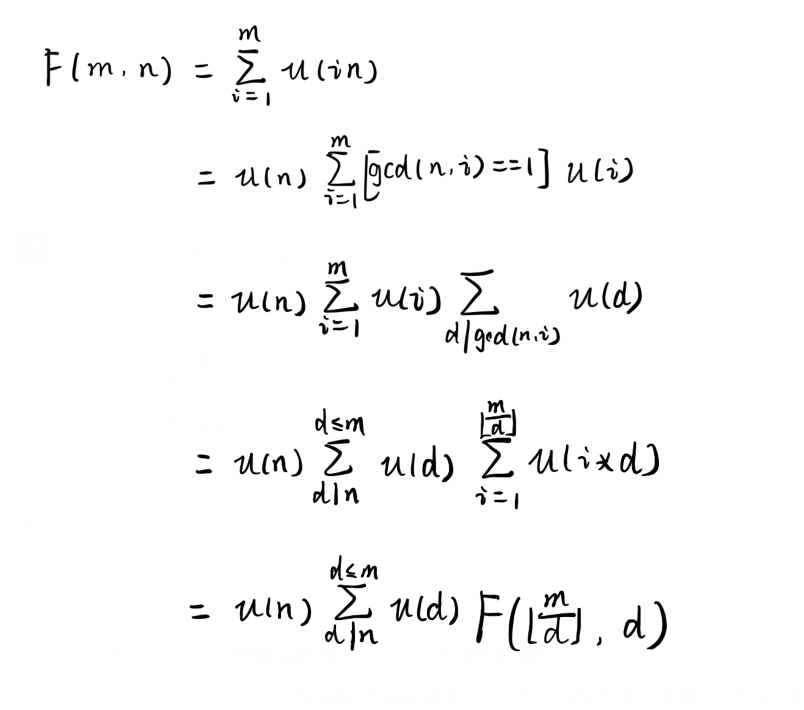
这样就可以进行递归了,但是我不会算复杂度...
还注意到一个地方,线筛的判断 i % prime[j] == 0 的地方要注意函数的取值
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
typedef long long ll;
ll prime[N], cnt, vis[N], mu[N], sum[N];
void init() {
mu[1] = 1;
for (int i = 2; i < N; i++) {
if (!vis[i]) {
prime[++cnt] = i;
mu[i] = -1;
}
for (int j = 1; j <= cnt and prime[j] * i < N; j++) {
vis[prime[j] * i] = 1;
mu[prime[j] * i] = -mu[i];
if (i % prime[j] == 0) {
//**这一行不能去掉**
mu[i * prime[j]] = 0;
break;
}
}
}
for (int i = 1; i < N; i++) sum[i] = sum[i - 1] + mu[i];
}
ll n, m;
unordered_map<ll, ll> M;
ll djs(ll n) {
if (n < N) return sum[n];
if (M.count(n)) return M[n];
ll ans = 1;
for (ll l = 2, r; l <= n; l = r + 1) {
r = n / (n / l);
ans -= (r - l + 1) * djs(n / l);
}
return M[n] = ans;
}
ll cal(ll n) {
int ans = 1;
if (n < N) return mu[n];
for (ll i = 2; i * i <= n;i++) {
if (n % i == 0) {
if (n % (i * i) == 0)
return 0;
ans *= -1;
n /= i;
}
}
if (n > 1)
ans *= -1;
return ans;
}
ll solve(ll m, ll n) {
if (n == 1) return djs(m);
ll v = cal(n);
if (v == 0) return 0;
ll ans = 0;
ll t = m < sqrt(n) ? m : sqrt(n);
for (ll d = 1; d <= t; d++) {
if (n % d == 0) {
ans += cal(d) * solve(m / d, d);
if (n / d <= m)
ans += cal(n / d) * solve(m / (n / d), n / d);
}
}
return v * ans;
}
int main() {
init();
scanf("%lld%lld", &m, &n);
printf("%lld
", solve(m, n));
}