ABC 187 F. Close Group

题意

给一个无向图， (N) 个顶点 (M) 条边， 问删除若干条边之后最少组成多少个连通分量，使得每个联通分量都是完全图。

(1 le N le 18) , (0 le M le dfrac {N(N-1)} 2)

思路

比赛的时候一直在想搜索，每次找出一个最大的完全子图，然后删掉，看删多少次。

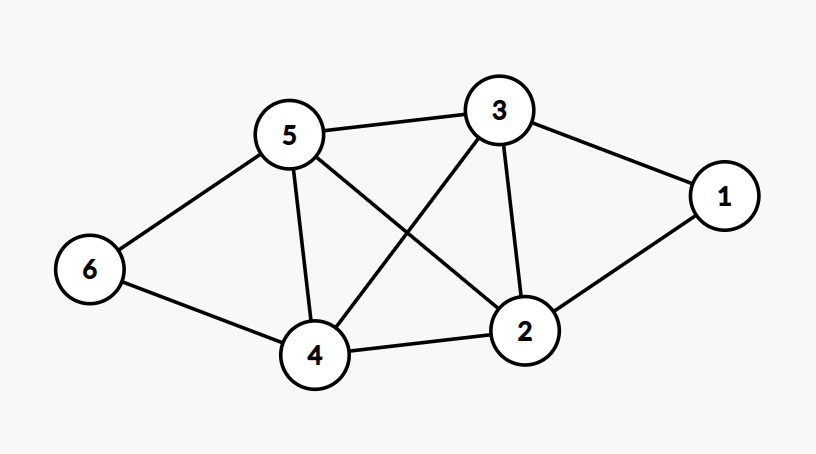
其实这样的想法是错误的，比如给出一个这样的图

实际上用两个联通分量 {4,5,6} 和 {1,2,3} 就可以了，如果找最大的就会找到 {2,3,4,5} {1} {6}

这样三个联通分量

解法

用 (O(n^22^n)) 复杂度预处理出所有完全子图， 然后枚举所有状态的子集转移即可

对于一个集合 (S) ,枚举它的所有子集 ：

for (int i = (S - 1) & S;i ;i = (i - 1) & S)

对于所有情况的所有子集，考虑有 (k) 个二进制位的数 (a) 这样的数有 (C_n^k) 个，子集有 (2^k) 个

所以所有的子集

[S = sum_{i = 0}^nC_n^i2^i = 3^n ]

所以这一步的复杂度是 (O(3^n))

总的复杂度是 (O(n^22^n + 3^n))

ps:

枚举 n 个 bit 中有 k 个 1 的枚举

#include<bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10;
typedef long long ll;

void print(int x,int n){
    for(int i = n - 1;i >= 0;i--){
        printf("%d", (x >> i) & 1);
    }puts("");
}
void EnumK(int k, int n)/*求出总共n个状态中，有k个状态为1的所有情况*/
{
    int x, y;
    for (int i = (1 << k) - 1;i < (1 << n);i = ((i & ~y) / x >> 1) | y) {
        print(i, n);
        x = i & -i, y = i + x;
    }
}

int main(){
    int k, n;
    while(cin >> k >> n){
        EnumK(k, n);
    }
}

#include<bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10;
typedef long long ll;
int g[20][20], f[1 << 18], n, m, x, y;
int main(){
    scanf("%d%d", &n, &m);
    while (m--) { 
        scanf("%d%d", &x, &y); 
        x--, y--; 
        g[x][y] = g[y][x] = 1;
    }
    memset(f, 0x3f, sizeof f);
    
    for(int i = 0;i < (1 << n);i++){
        bool ok = true;
        for(int j = 0;j < n;j++){
            if (!((i >> j) & 1))continue;
            for(int k = j + 1;k < n;k++){
                if (!((i >> k) & 1)) continue;
                if(!g[j][k]){
                    ok = false;
                    break;
                }
            }if (not ok)break;
        }
        if (ok)f[i] = 1;
    }
    
    for(int i = 0;i < (1 << n);i++){
        for(int j = (i - 1) & i;j ;j = (j - 1) & i){
            f[i] = min(f[i], f[j] + f[i ^ j]);
        }
    }
    printf("%d
", f[(1 << n) - 1]);
}