对于见得多了的东西,我往往就习以为常了,慢慢的就默认了它的存在,而不去思考内在的一些道理。总体最小二乘是一种推广最小二乘方法,本文的主要内容参考张贤达的《矩阵分析与应用》。
1. 最小二乘法
最小二乘法,大家都很熟悉,用在解决一超定方程。最小“二”乘的“二”体现在准则上——令误差的平方和最小,等价于
最小二乘解为(非奇异)
可以从多个角度来理解最小二乘方法,譬如从几何方面考虑,利用正交性原理导出。
Steven M.Kay 的《统计信号处理—估计理论》中是这样介绍最小二乘估计的:最小二乘估计特点在于对观察数据没有任何概率假设,只需要假设一个信号模型,因此它不是最佳的,如果没有对数据的概率结构做出假设,其统计性能也是无法评判的。(实际上LSE可能是MVU,说不是最佳有些不妥)
当然,我们希望能够分析最小二乘解的特性,即使不能对其进行全面的评判,至少需要了解其应用范围和特点。
2. 稳定性分析
一个好的估计往往具有无偏和最小方差的特性(或是渐进无偏的,譬如最大似然估计)。Gauss-Markov定理告诉我们,对于数据向量具有加性噪声或者扰动的超定方程
,如果误差向量满足以下条件,此时最小二乘解是无偏且具有最小方差的。
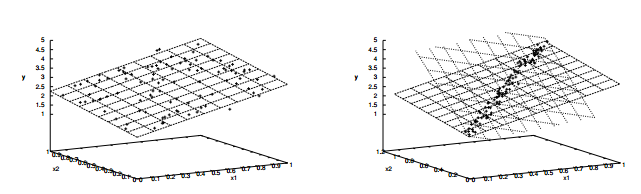
定理证明可见张贤达《矩阵分析与应用》p406页。这一结论表明,最小二乘解是一个很好的估计,那么问题出现在哪呢?我们注意到,采用最小均方误差准则的线性回归(Linear regression)和最小二乘解具有相同的形式。《Machine Learning plus Intelligent Optimization》书中有这样一幅图显示了线性回归中存在的稳定性问题。
左图表示一个好的数据集合能够确定一个稳定的平面。右图中,不恰当的取样点使得微小的扰动会导致大的结果的偏差。 然而往往数据集的分布是不可控的。
稳定性指数据小的扰动只会导致小的结果偏差。一个良态问题(well-posed problem)是稳定的,然而实际上的问题往往是病态(ill-posed)。为此,在线性回归以及其他多种解决问题方案中采用了正则化方法。广为应用的方法是Tichonov regularization,思想在于利解的先验知识使解稳定,即假设解是光滑的。关于正则化问题,可以参考Simon Haykin的《神经网络原理》,此处不做讨论。对于稳定性分析,或者说数值稳定性,《矩阵分析与应用》p342进行了详细的讨论。
(矩阵)数值稳定性
研究矩阵,其中
或
发生扰动时,解向量如何发生变化?讨论得到以下结果
由此可见,影响解向量变化的重要参数是,我们将其记为条件数,记作
这就是矩阵的条件数的定义,由上式易知,条件数刻画了误差经过矩阵后扩大为解向量误差的程度。当系数矩阵一个很小扰动只会引起解向量很小变化的时候,我们将矩阵称为是“良态”的,反之称为是“病态”的。
正定矩阵的Cholesky分解这篇文章中提到了矩阵的“良态”和特征值之间的关系,此处我并没有进行太多思考,有兴趣的话可以去看看特征值扩散度相关知识。wiki百科上给出的例子表明,如果采用2-范数,条件数可以记为
其中代表的是矩阵的奇异值。
最小二乘法中对于超定方程实际求解的是,条件数表示为
也就是说,误差对方程解的影响和
的条件数的平方成反比,这显然是我们不愿意看到的。采用正则化方法实际求解的是
,由上可知条件数下降了(从2-范数来看,分子分母同时加上了
)。
3.总体最小二乘
如果说模型是完全正确的,我们根本不需要考虑算法的稳定性(当然,由于计算机计算时会有截位,所以这是不可能的)。道理很简单,没有扰动,为何需要分析稳定性呢?这充分说明了,最小二乘没有考虑到扰动的存在,因此其稳定性较差是情有可原的。
可以对矩阵有扰动情况下,最小二乘的性能进行分析,矩阵的扰动矩阵非零情况下,
一般有偏。且可以证明(p407)
如果为零均值,方差为
的独立同分布噪声,
为零均值,方差为
的独立同分布噪声。此时最小二乘解方差相对于矩阵无扰动下增加倍数等于
我们知道其根源在于没有考虑矩阵的扰动,在这一情况下,为了克服最小二乘的缺点,引入了总体最小二乘方法。
总体最小二乘思想在于分别使用扰动向量和扰动矩阵去修正和
中的扰动。也就是说,总体最小二乘解决以下问题
其中为扰动矩阵,
,此处范数采用Frobenius范数。
利用增广矩阵的奇异值分解可以求得总体最小二乘解。(只讨论超定方程情况)其中分为两种情况:只有一个最小的奇异值时有一组解,最小奇异值多重或者后面若干个非常接近时求解某一意义下的最小二乘解。即
应该是非满秩矩阵(由于噪声存在,一般都是满秩的),因此对应最小特征值的特征向量就是总体最小二乘解,多个相同最小二乘解时特征向量有多个,因此加上其他约束求解。具体方法本文不做论述。
4.TLS解释和分析
真正吸引人的不是TLS的解法,而是它到底为何能够(在一定条件下)弥补LS的缺点?(虽然从其推导过程中感觉是有效的)即使有效,那么原因是什么呢?
张贤达书p414页神奇的推导出了这么一个结果(不可逆情况下求伪逆,此时有其他诸如最小范数的约束)
第一眼看到这个结果的时候,我想:怎么可能?正则化中的加法很有道理,这里的减法不是会让情况更差吗?但是这里的解释很有道理
总体最小二乘可以解释为一种具有噪声消除的最小二乘方法,先从协方差矩阵中减去噪声影响项,然后再对矩阵求逆求解,得到最小二乘解。
那么问题出在哪呢?我们注意到正则化中的是任意选取的,或者说不是“任意”,也是和矩阵
没有多大关系的。然而此处的
实际上是矩阵
的奇异值中的最小的那个,由于TLS采用了完全不同的思路,出现相异的结果也就不足为奇了。
我们再对TLS进行详细的分析,实际上,所以
至少应该有一个特征值为零的。由于噪声的存在,这一要求往往是达不到的。假设噪声是高斯白且独立同分布,那么噪声的自相关矩阵是对角阵,也就相当于在所有特征值上加上了一个固定的常数,这个常数就是噪声的方差。一般而言
是实数,其特征值都是正数,所以我们可以认为最小的特征值(多个最小则都取)实际上就是噪声的方差。这些特征值对应的特征函数构成的线性空间被称为噪声子空间。总体最小二乘就是去除了噪声的最小二乘,从这一点上看,TLS对矩阵
的扰动有抑制作用,即TLS的更加接近无扰动子空间。
对于扰动敏感度分析,可参考《矩阵分析与应用》p416。
5.总结
接触这一方法的时间不长,如有错误,还请大家指正。本文只对其进行了理论上的分析,就我接触而言,在谱分析中总体最小二乘应用广泛,不知在其他应用上是否能够取得好的效果。就线性回归而言,一般情况下正则化方法应该会有更好的效果,总体最小二乘还是有太多的假设了。不知这一结论是否正确,还请大家指明或仿真分析。
但毋庸置疑的是,总体最小二乘在很多地方都取得了很好的效果,或许还能够得到更广泛的应用。同时,最重要的是在这一过程中我深刻的体会到了对越熟悉的东西要越了解,而不是麻木。
算法对扰动的敏感度要低,我们对算法的敏感度要高才好。