程序说明 V0.0 2015/1/24 | LDPC译码算法代码概述 |
概述 |
本文介绍了包括LDPC_Simulation.m, ldpcdecoderbp1.m,ldpcdecoderminsum.m, ldpcdecoderbp2.m,ldpcdecoderminsum2.m在内的MATLAB代码的编写思路,基本原理和功能,具体代码可见文后。本文暂不涉及LDPC校验矩阵的构造和编码程序,此部分由他人提供。 |

修订历史 | 以下表格展示了本文档的修订过程
|

简介 |
本程序基于MATLAB 2014a 编写,本文档中提到的"MATLAB"均指该特定版本MATLAB。本文提到的LDPC编码均指二进制LDPC编码,多进制暂时不进行讨论。 LDPC(低密度奇偶校验)编码,顾名思义有两个特性:纠错编码采用奇偶校验,该种编码方式具有低密度的特点。在学习LDPC编码之前,必须要对线性分组码的基本概念有详细的了解,包括线性分组码的映射思想、生成矩阵、校验矩阵等。这部分内容可参考《通信原理》等书籍。有限域上的编码可不做了解,这一点我现在也不懂。 低密度的意思是对于校验矩阵H而言,1的个数远小于0的个数。这对于译码算法而言是至关重要的,这表现在两个方面。其一是对于一个大的校验矩阵而言,太多的1会导致计算上的困难;其二是译码算法(此处特指置信传播类算法)中的很多假设实际上是不成立的,在H不满足低密度约束下对其性能会有很大影响。 LDPC的置信传播算法包括以下假设:
关于置信传播的具体原理和假设将在《学习笔记:LDPC编译码基本原理》中做具体阐述,此处不再详细说明。(由于《学习笔记:LDPC编译码基本原理》还未开始撰写,该部分内容可能会有较大变动) |

程序设计 |
程序结构 校验矩阵和编码程序已经给定程序(脚本)按顺序由以下几个部分构成
校验矩阵已知,且命名为H(800,480).mat,采用load('H(800,480).mat')即可载入,校验矩阵为H。随机序列(数据)生成和编码采用ldpcencoder(H)调用函数,返回数据及其编码。本文仅对AWGN信道和译码程序做说明。
AWGN信道 加性高斯白噪声信道,说明信道的仿真只需要加上一个高斯白噪声就可以了。"白"意味着任意两个不同时刻的噪声都是不相关的,"高斯"即服从高斯分布,满足这两个要求很简单,采用randn生成一组序列即可。唯一不确定的就是噪声的方差了。 对于零均值信号而言,方差代表的就是功率。问题就转变成了如何通过EbN0计算噪声的功率?EbN0是一个比值,每比特能量/噪声功率谱密度。如果我们将信号功率归一化,那么噪声功率就是信噪比SNR的倒数。
在本程序中,校验矩阵为480×800(比特速率为码速率的0.4),采样频率等于码速率(带宽为采样频率的一半),因此有 SNR_dB = EbN0_dB((nEbN0)) + 10*log10(2)+10*log10(0.4);
译码程序编写思想(置信传播为例) 译码算法实际上是很简单的,问题在于呢,如何早到那些要乘的数。就是下式中所表现的
对于这个问题,有两个考虑方式: 1. 传播都是在边上的,那么从边入手。 H矩阵中有多少个非零元素,就有多少条边,记为L。对于每一条边而言,用两个个长度也为L的向量保存边所连接的变量节点和校验节点的编号(r_Mark,c_Mark)。 初始化: 变量节点传递的信息是P(X|Y),那么只需要知道边所对应的变量节点(c_Mark(l))就知道了传递的信息。 迭代: 对于每一次的迭代,从第一条边开始。找出边的r=r_Mark(l),之后找到所有的r_Mark = r的边,计算校验节点的信息。 同理计算变量节点传播的信息 判决 ……
问题在于: 找在MATLAB中采用find就可以了,但是复杂度到底是多少呢?每个循环都要find一下实在是太浪费了……
2. 利用H矩阵的天然结构 也就是说实际上我们要取的集合是H对应的每一行或每一列的数。如果我们采用和H矩阵完全相同的方式去构造信息传递的两个矩阵,那么在寻址的过程中将会容易很多。 想法1对应的程序是ldpcdecoderbp1和ldpcdecoderminsum,想法2对应的程序是ldpcdecoderbp2和ldpcdecoderminsum2。实验证明,程序对应的校验矩阵如本代码所附时,采用方式1运行效率高。 |

算法 |
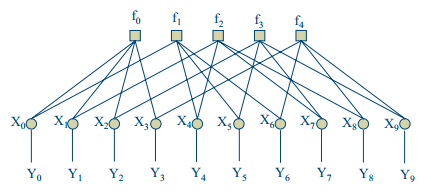
置信传播 以下内容是置信传播算法的编程具体实现方式,按上述思路1编写对应ldpcdecoderbp1 LDPC译码过程可以用Tanner图直观表示,如图 1所示,接收到的序列表示为
图 1 Tanner图
本文不叙述过多原理性问题,仅列出计算步骤,此处假定编码后的星座映射为 1.初始化:(P0,P1 = 1-P0)
2.校验消息处理:(校验节点传递信息rmn0,rmn1 = 1-rmn0) 3.变量消息处理:(k为归一化常数) 4.译码判决:(求0,1后验概率之比值qn0_1,大于1判决为0) 如果满足 最小和算法 以下内容是最小和算法的编程具体实现方式,按上述思路2编写,对应ldpcdecoderminsum2。 对于最小和算法,尤其要注意的是发送端的映射关系。对于置信传播算法而言,如果把关系搞错了,会发现误码率大约是1减正确情况下误码率,这个时候很快就能发现毛病所在;但在最小和中,弄错了的话,误码率会变得怪怪的。 最小和算法本质上和置信传播没有什么区别。正如我们所观察到的,置信传播算法中有两个可以改进的地方:其一是对于概率来说,不是0就是1,没有必要采用两组变量,更好的选项可能是采用比值的形式;其二是算法中采用的乘法取对数之后会变成加法,这样能减少运算量。从这两点出发,提出了对数似然比算法,最小和算法实际上是对数似然比算法的近似。 同置信传播算法的前提假设,但以想法2为例,最小和算法阐述如下。 1.初始化: (按校验矩阵结构对应vl至vnm)
2.校验消息处理:(校验节点传递信息unm) 3.变量消息处理:(变量节点) 4.译码判决:(qn0_1,大于0判决为0) 如果满足 |

改进思路 |
改进的意思是这一程序是对的,但是能够做得更好。译码程序的初步验证过程是将EbN0设置为一个较大的值,在这一情况下迭代次数应该是1。很显然这里的四个译码函数都完成了这一个测试,但是否真正无误还有待更进一步的考验。 做得更好的"好"往往是必须有一个标准的,如果我们将程序计算复杂度和空间复杂度降低、且易于FPGA实现作为"好"的标准,那么可以从以下几个方面改进
|

参考 |
《LDPC码基础与应用》 贺鹤云 An Introduction to Low-Density Parity Check Codes Daniel J. Costello, Jr. |

代码 | …… |

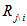 集合中的数据
集合中的数据
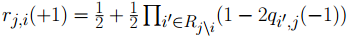
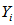 ,校验节点为
,校验节点为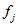 ,我们要求的是
,我们要求的是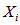 的条件后验概率。
的条件后验概率。
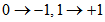 。
。
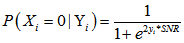
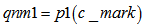
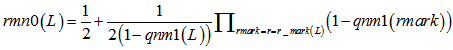
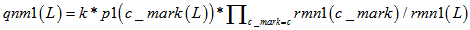
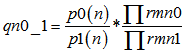
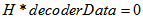 或达到最大迭代次数,返回译码后结果,退出循环;否者回到步骤2。
或达到最大迭代次数,返回译码后结果,退出循环;否者回到步骤2。
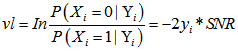
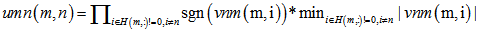

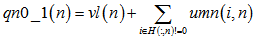
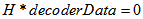 或达到最大迭代次数,返回译码后结果,退出循环;否者回到步骤2。
或达到最大迭代次数,返回译码后结果,退出循环;否者回到步骤2。