栈——C语言模拟
一、定义
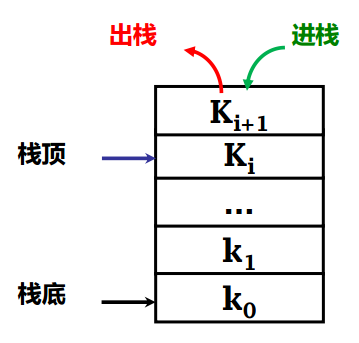
根据wiki百科,栈(stack),是一种特殊的串列形式的数据结构,是线性表的一种,一种_限制访问端口_的线性表。
栈的特殊之处在于只能在链接串列的一端,即栈顶(top)进行操作,在栈顶进行存入数据(push),取出(pop).
推入:将数据放入栈的顶端,top+1.
弹出:将顶端数据资料输出,top-1.
也就是所谓的先进后出(LIFO,Last In First Out).
栈的存在价值
虽然说,栈实现的功能用数组和链表也可以实现,不过你不得不分神到考虑数组的下标增减、链表的指针指向等问题。
引用原作者的例子,就像我们明明有两只脚可以走路,算上游泳,理论上可以去到全球任何一个地方,那么为什么我们还要有汽车、火车、飞机一样。在向未来的发展过程中,我们需要考虑的更多的是在在抵达目的地之后的发展,这个抵达的过程已经成了我们继续发展的拖累。这时,优化移动方式就成了必然,让我们得以关注结果之后。
所以说,栈的引入简化了程序设计的问题,划分了不同关注层次,让人更聚焦于问题本身。比如C++,JAVA等的标准库都封装了栈的结构。
栈分为顺序栈和链式栈
两者的差别在哪里呢?为什么要特别用两种方法模拟呢?
时间复杂度上,两者都没有任何其他的操作,均为O(1);
而空间复杂度上,顺序栈只存储了数据和表头标记;而链式栈对每个数据都建立了一个节点,存储数据之外还存储了指向下一个节点的指针,空间较顺序栈多了一倍。
所以顺序栈优点,空间占用小,存取定位还是比较方便的,在使用小空间的;而链式栈可以
以下是栈的抽象数据类型的定义:
ADT Stack{
数据对象:D={ai|ai in ElemSet,i = 1,2,...,n, n >= 0}
数据关系:R1={<a(i-1),ai>|a(i-1),ai in D, i = 2,..,n}
约定an端为栈顶,ai端为栈底.
基本操作:
InitStack(&S)
操作结果:构造一个空栈S
Destroy(&S)
初始条件:栈S已存在。
操作结果:栈S被销毁。
ClearStack(&S)
初始条件:栈S已存在。
操作结果:将S清为空栈。
StackEmpty(S)
初始条件:栈S已存在。
操作结果:若栈S为空栈,则返回TRUE,否则FALSE。
StackLength(S)
初始条件:栈S已存在。
操作结果:返回S的元素个数,即栈的长度。
GetTop(S,&e)
初始条件:栈S已存在且非空。
操作结果:用e返回S的栈顶元素。
Push(&S,e)
初始条件:栈S已存在。
操作结果:插入元素e为新的栈顶指针。
Pop(&S,&e)
初始条件:栈S已存在且非空。
操作结果:删除S的栈顶元素,并用e返回其值。
StackTraverse(S,visit())
初始条件:栈S已存在且非空。
操作结果:从栈底到栈顶依次对S的每个数据元素调用函数visit()。一旦visit()失败,则操作失效。
}ADT Stack
二、顺序栈
定义:
typedef struct{
SElemType *base;
SElemType *top;
int stacksize;
}SqStack;
接下来是顺序栈的模块说明
#define STACK_INIT_SIZE 100 //存储空间初始分配量
#define STACKINCREMENT 10 //存储空间分配增量
#define ERROR 0
#define OK 1
#define OVERFLOW -1
typedef struct{
SElemType *base; //在栈构造之前和压栈之后,base的值为NULL
SElemType *top; //栈顶指针,指向栈顶的下一个位置
int stacksize; //当前已分配的存储空间,以元素为单位
}SqStack;
//------基本操作的函数原型说明------
Status InitStack(SqStack &S);
//构造一个空栈S
Status DestroyStack(SqStack &S);
//销毁栈S,S不再存在
Status ClearStack(SqStack &S);
//把S置为空栈
Status StackEmpty(SqStack S);
//若栈S为空栈,则返回TRUE,否则返回FALSE
int StackLength(SqStack S);
//返回S的元素个数,即栈的长度
Status GetTop(SqStack S,SElemType &e);
//若栈不空,则用e返回S的栈顶元素,并返回OK;否则返回ERROR
Status Push(SqStack &S,SElemType e);
//插入元素e为新的栈顶元素
Status Pop(SqStack &S,SElemType &e);
//若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR
Status StackTraverse(SqStack S,Stack (*visit()));
//从栈底到栈顶一次对栈中每个元素调用函数visit().一旦visit()失败,则操作失败
/***************基本操作的算法描述**********/
Status InitStack(SqStack &S){
//构造一个空栈
S.base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));
if(!S.base) exit(OVERFLOW);
S.top = S.base;
S.stacksize = STACK_INIT_SIZE;
return OK;
}//InitStack
Status GetTop(SqStack S, SElemType &e){
//若站不空,则用e返回S的栈顶元素,并返回OK;否则返回ERROR
if(S.top == S.base) return ERROR;
e = *(S.top-1);
return OK;
}//GetTop
Status Push(SqStack &S,SElemType e){
//插入元素e为新的栈顶元素
if(S.top-S.base >= S.stacksize){
//栈满,追加存储空间
S.base=(SElemType *)realloc(S.base,(S.stacksize+STACKINCREMENT)*sizeof(SElemType));
if(!S.base) exit(OVERFLOW);//存储分配失败
S.top=S.base+S.stacksize;
S.stacksize+=STACKINCREMENT;
}
*S.top++ = e;
return OK;
}//push_back
Status Pop(SqStack &S,SElemType &e){
//若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK,否则返回ERROR
if(S.top == S.base) return ERROR;
e = * --S.top;
return OK;
}//pop
顺序栈是为栈预先分配一个大小固定且较合适的空间,最常见的做法是Stack结构中含一个数组。
struct stack{
int data[10];
int top;
};
以下是数组实现的各函数代码
#include <stdio.h>
#include <stdlib.h>
#define STACK_POP_ERR 42
#define stack struct Stack;
struct Stack{
int val[10];
int top; //栈顶
};
/* 检查栈是否为空 */
int empty(stack *stk) {
return stk->top == 0;
}
/* 推入资料 */
void push(stack *stk, int x){
stk->top=stk->top+1;
stk->val[stk->top]=x;
}
/* 弹出并返回资料 */
int pop(stack *stk) {
if(empty(stk))
return STACK_POP_ERR; // 不能弹出
else{
stk->top=stk->top-1;
return stk->val[stk->top+1];//这里使用了复用技术
}
}
int main(){
// 宣告并初始化空间
stack stk;
stk.top=0;
// 推入四个
push(&stk, 3);
push(&stk, 4);
push(&stk, 1);
push(&stk, 9);
// 弹出三个
printf("%d ", pop(&stk));
printf("%d ", pop(&stk));
printf("%d ", pop(&stk));
return 0;
}
三、链式栈
链式栈是定义一个结构体,去掉表头(表头是指一个空节点只带有一个指向存储栈顶数据的空间的指针,即首节点就开始存储数据)
链式栈这里我用二进制转八进制的程序来说明
#include <stdio.h>
#include <stdlib.h>
#define ERROR 0
#define OK 1
typedef struct node{
int data;
struct node* nextPtr;
}Stack,*LinkStack;
int StackDel(LinkStack &s){
if (NULL == s) return ERROR;//判断栈是否出现了意外的空的状态
LinkStack temp = s;//定义一个存储即将被释放的空间的指针
s = s->nextPtr;//
free(temp);
return OK;
}
int pop(LinkStack &s){
int e;
if (NULL == s)
return ERROR;
e = s->data;//存储从栈中取出的值
StackDel(s);//删除已取出的栈的空间
return e;
}
int push(LinkStack &s, int e){
LinkStack p = (LinkStack)calloc(1, sizeof(Stack));//动态分配空间并初始化
if (!p){
printf("Error calloc_push");
return ERROR;
}
p->data = e;
p->nextPtr = s;//将新数据链接到链表头部
s = p;
return OK;
}
void transform(LinkStack &s){
int e, temp = 0, pow = 1;
while (NULL != s){//直到栈空
e = pop(s);
temp += e*pow;//进行二进制转十进制的计算
pow *= 2;//进行位权的累乘
}
printf("The octonary answer is:(");
printf("%o", temp);//输出八进制结果
printf(")8
");
}
void input(LinkStack &s){
char ch;
printf("Please input the binary string:");
while (scanf("%c", &ch) && ch != '#'){
push(s, ch - '0');//将字符型二进制数以整型输入
}
return;
}
int main(){
//freopen("input.txt","r",stdin);
//freopen("output.txt","w",stdout);
LinkStack s = NULL;//栈的头结点指针
input(s);
transform(s);
return 0;
}
四、栈的应用
1.表达式求值
2.由递归到非递归
3.深度优先搜索(bfs)
参考资料:
[1].kelinlin.为什么要使用栈这种数据结构.
[2]Wikipedia Definition.
[3]《数据结构》,严蔚敏