在机器学习中,我们通常会根据输入 (x) 来预测输出 (y),预测值和真实值之间会有一定的误差,我们在训练的过程中会使用优化器(optimizer)来最小化这个误差,梯度下降法(Gradient Descent)就是一种常用的优化器。
什么是梯度
梯度是一个向量,具有大小和方向。想象我们在爬山,从我所在的位置出发可以从很多方向上山,而最陡的那个方向就是梯度方向。
对函数 (f(x_1, x_2, ..., x_n)) 来讲,对于函数上的每一个点 (P(x_1,x_2,...,x_n)),我们都可以定义一个向量 ({frac{partial{f}}{partial{x_1}}, frac{partial{f}}{partial{x_2}}, ...,frac{partial{f}}{partial{x_n}} }),这个向量被称为函数 (f) 在点 (P) 的梯度(gradient),记为 (
abla{f(x_1, x_2, ...,x_n)}) 。函数(f)在(P)点沿着梯度方向最陡,也就是变化速率最快。比如对于二元函数 (f(x, y))来讲,我们先将函数的偏导数写成一个向量 ({frac{partial{f}}{partial x},frac{partial{f}}{partial y}}),则在点 ((x_0, y_0))处的梯度为 ({frac{partial{f}}{partial{x_0}},frac{partial{f}}{partial{y_0}}})。
梯度方向是函数上升最快的方向,沿着梯度方向可以最快地找到函数的最大值,而我们要求误差的最小值,所以在梯度下降中我们要沿着梯度相反的方向。
梯度下降步骤
假设我们要求函数 (f(x_1, x_2))的最小值,起始点为 (x^{(1)} = (x_1^{(1)}, x_2^{(1)})),则在 (x^{(1)}) 点处的梯度为 ( abla(f(x^{(1)})) = (frac{partial{f}}{partial{x_1^{(1)}}},frac{partial{f}}{partial{x_2^{(1)}}})),我们可以进行第一次梯度下降来更新x:
其中,(alpha) 被称为步长。这样我们就得到了下一个点(x^{(2)}), 重复上面的步骤,直到函数收敛,此时可认为函数取得了最小值。在实际应用中,我们可以设置一个精度 (epsilon), 当函数在某一点的梯度的模小于 (epsilon) 时,就可以终止迭代。
一个例子
使用梯度下降求函数 (f(x, y) = x^2+y^2) 的最小值。
首先求得函数的梯度:
def get_gradient(x, y):
return 2*x, 2*y
然后迭代:
def gradient_descent():
x, y = 5, 5 #起始位置
alpha = 0.01
epsilon = 0.3
grad = get_gradient(x, y)
while x**2+y**2 > epsilon**2:
x -= alpha*grad[0] # 沿梯度方向下降
y -= alpha*grad[1]
print("({},{})取值为{}".format(x, y, x**2+y**2) )
最后的结果:
(0.20000000000000104,0.20000000000000104)取值为0.08000000000000083
真实最小值在(0,0)点取得,最小值为0,两者非常接近(上面的epsilon设置的比较大,当epsilon很小时,最后的结果会非常接近0)。
梯度下降分类
以线性回归为例,假设训练集为 (T={(x_1, y_1), (x_2, y_2),..., (x_N,y_N)}),其中(x_i∈mathbb{R}^n),是一个向量,(y_i∈mathbb{R})。我们通过学习得到了一个模型 (f_M(x,w) = Sigma_{j=0}^M w_ix^i),可以根据输入值 (x) 来预测 (y) ,预测值和真实值之间会有一定的误差,我们用均方误差(Mean Squared Error, MSE)来表示:
(L(w))被称为损失函数(loss function),加 1/2 的目的是为了计算方便, (w)是一个参数向量。
根据梯度下降时使用数据量的不同,梯度下降可以分为3类:批量梯度下降(Batch Gradient Descent,BGD)、随机梯度下降(Stochastic Gradient Descent, SGD)和小批量梯度下降(Mini-Batch Gradient Descent, MBGD)。
批量梯度下降(SGD)
批量梯度下降每次都使用训练集中的所有样本来更新参数,也就是
更新方法为
当样本数据集很大时,批量梯度下降的速度就会非常慢。
优点:可以得到全局最优解
缺点:训练时间长
随机梯度下降(SGD)
每次梯度下降过程都使用全部的样本数据可能会造成训练过慢,随机梯度下降(SGD)每次只从样本中选择1组数据进行梯度下降,这样经过足够多的迭代次数,SGD也可以发挥作用,但过程会非常杂乱。“随机”的含义是每次从全部数据中中随机抽取一个样本。这样损失函数就变为:
参数更新方法同上:
优点:训练速度快
缺点:准确度下降,得到的可能只是局部最优解
小批量梯度下降(MBGD)
小批量梯度下降是 BGD 和 SGD 之间的折中,MBGD 通常包含 10-1000 个随机选择的样本。MBGD降低了了SGD训练过程的杂乱程度,同时也保证了速度。
在线性回归中使用梯度下降
这一部分将介绍一个使用梯度下降来进行线性回归的例子。
数据如下:
import numpy as np
import matplotlib.pyplot as plt
% matplotlib inline
N = 10 # 数据量
x = np.random.uniform(0, 5, N).reshape(N,1)
y = 2*x + np.random.uniform(0,2,N).reshape(N,1)
plt.scatter(x, y)
我们在(0,5)之间随机生成了10组数据,如下:
我们将对这十组数据进行线性回归。
从图像上我们可以看到 x 和 y 满足线性关系,所以我们将模型定义为 (f(x, w) = wx = w_1x+w_2),然后使用均方误差来定义损失函数:
对应代码如下:
def loss_function(omega, x, y):
diff = np.dot(x, omega) - y
loss = 1/(2*N)*(np.dot(np.transpose(diff), diff))
return loss
因为要计算(f(x, w) = wx = w_1x+w_2),为了表示方便,我们将 (x = (x_1, x_2, ..., x_N)^T)扩充为 (x=((x_1,x_2,...,x_n), (1,1,...,1))^T),对应下面的代码:
ones = np.ones((N, 1))
x = np.hstack((x, ones))
对(w)求导可得:
写成向量的形式:
对应下面的代码:
def loss_gradient(omega, x, y):
diff = np.dot(x, omega) - y
gradient = (1./N)*(np.dot(np.transpose(x), diff))
return gradient
由于数据量比较少,这里使用批量梯度下降的方法(BGD),代码如下:
def BGD():
alpha = 0.01
omega = np.array([1, 1]).reshape(2, 1) #omega初值
gradient = loss_gradient(omega, x, y)
epsilon = 1e-3
while np.linalg.norm(gradient) > epsilon:
omega = omega - alpha * gradient
gradient = loss_gradient(omega, x, y)
return omega
测试代码:
result = BGD()
print("result={}".format(result))
x1 = np.linspace(0, 5, 10)
y1 = result[0]*x1 + result[1]
plt.scatter(x[:,0], y)
plt.plot(x1, y1)
结果:
result=[[2.15366003]
[0.69151409]]
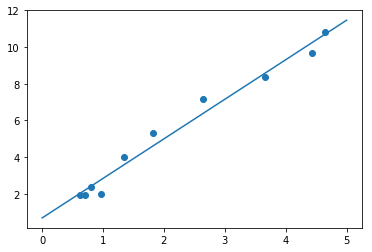
可以看到,我们使用梯度下降成功用一条直线拟合了这些数据。
完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
% matplotlib inline
N = 10 # 数据量
x = np.random.uniform(0, 5, N).reshape(N,1)
y = 2*x + np.random.uniform(0,2,N).reshape(N,1)
plt.scatter(x, y)
ones = np.ones((N, 1))
x = np.hstack((x, ones))
def loss_function(omega, x, y):
diff = np.dot(x, omega) - y
loss = (1./2*N)*(np.dot(np.transpose(diff), diff))
return loss
def loss_gradient(omega, x, y):
diff = np.dot(x, omega) - y
gradient = (1./N)*(np.dot(np.transpose(x), diff))
return gradient
def BGD():
alpha = 0.01
omega = np.array([1, 1]).reshape(2, 1) #omega初值
gradient = loss_gradient(omega, x, y)
epsilon = 1e-3
while np.linalg.norm(gradient) > epsilon:
omega = omega - alpha * gradient
gradient = loss_gradient(omega, x, y)
return omega
result = BGD()
print("result={}".format(result))
x1 = np.linspace(0, 5, 10)
y1 = result[0]*x1 + result[1]
plt.scatter(x[:,0], y)
plt.plot(x1, y1)
总结
梯度下降法是一种常用的优化器,梯度可以理解为多元函数偏导数组成的向量(一元函数就是导数),沿着梯度方向函数增加最快,在梯度下降中要沿着梯度相反的方向。根据训练周期使用的数据量的不同,梯度下降可以分为批量梯度下降(BGD)、随机梯度下降(SGD)和小批量梯度下降(MBGD)。