嵊州D2T3
玛利亚∙多斯普拉泽雷斯
公墓一共有 n 个墓地,通过 n − 1 条通道相连。
每次,推销员可以在选择一个墓地推销给玛利亚。
但是,考虑很多的玛利亚会尽量否决这个提议。
她会选择一个墓地,否决掉它和与它相连的墓地。
但为了礼仪,玛利亚不会选择推销员推销的或者已经被否决的墓地。
同样,为了礼仪,推销员也不会推销已经被否决的墓地。
如果某个被推销的墓地没有被否决,那么销售员就胜利了。
否则玛利亚就胜利了。
除此之外,玛利亚可以在任意时间以洪水为借口删除一些通道,每次删除的通道数量也是任意的,不过删除的通道总数不能超过 K。
两个墓地相连意味着这两个墓地由一条通道直接连接。
请判断双方都在最优策略下,谁能获胜。
Input
第一行两个整数 n, K,表示墓地数和允许删除的通道数量。
接下来 n−1 行,每行两个整数 ui , vi,表示 ui 号墓地与 vi 号墓地之间有一条通道。
Output
输出一行。
如果推销员胜利,输出’salesman’,否则输出’Maria’(不包括引号)。
Examples
| cemetery.in | cemetery.out |
| 2 1 1 2 | Maria |
Notes
对于所有数据,满足 0 ≤ K < n ≤ 5000。
Subtask1[10pts]
n ≤ 3
Subtask2[25pts]
n ≤ 6
Subtask3[30pts]
K = 0
Subtask4[35pts]
无特殊限制
Solve!
自言自语
我看完Solution后,想很煞笔的说句:
我怎么没听过“博弈”呀?
原来,是我蒻爆了。。。
题目解析
A:salesman B:Maria
给出一棵树
每次 A 可以选择一个点染 A
B 可以选择一个点把它和与它相邻的点染 B
B 可以在任何时候去掉一些边,
但总数不超过一个定值k
染过的点不能选择,但是染色标记可以覆盖
若最后所有点都染 B 色,B 赢,否则 A 赢
解题思路
这种题目可以按照Subtask一个一个想
Subtask1[10pts]
n ≤ 3
几个分类讨论就好啦
Subtask2[25pts]
n ≤ 6
首先可以发现边不管什么时候去掉 都是一样的
所以可以先枚举去边的情况,再进行搜索
Subtask3[30pts]
K = 0
可以发现,当且仅当 n = 2,赢
Subtask4[35pts]
无特殊限制
若原树不存在完美匹配,A 一定赢
A 每次操作可以强迫 B 和他一起染掉一个匹配
最后肯定会剩下孤立点,A 再选这个点就是 A 色了
若存在,A 可以第一步强迫 B 破坏掉完美匹配的性质,依然 A 赢
结论 2:若 K = 0 , N ≥ 3,A 赢
但是我还是想知道:
完美匹配又是什么呢?
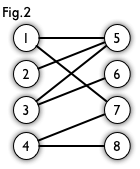
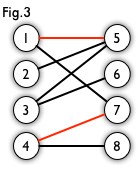
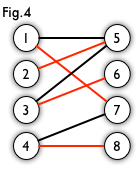
在图论中,一个「匹配」(matching)是一个边的集合,其中任意两条边都没有公共顶点。
例如,图 3、图 4 中红色的边就是图 2 的匹配。
A 每次操作可以强迫 B 和他一起染掉一个匹配
最后肯定会剩下孤立点,A 再选这个点就是 A 色了

(图片来源:http://www.renfei.org/blog/bipartite-matching.html)
举例来说:
如下图所示,如果在某一对男孩和女孩之间存在相连的边,就意味着他们彼此喜欢。
是否可能让所有男孩和女孩两两配对,使得每对儿都互相喜欢呢?

图论中,这就是完美匹配问题。
如果换一个说法:最多有多少互相喜欢的男孩/女孩可以配对儿?
这就是最大匹配问题。
就是说,你要把一堆的点的连线中,删去一些,最后要求:每个点有且仅有一个出边。
所以他们要两两双向思嘛~呵呵呵o(* ̄︶ ̄*)o
但是,怎么求他们能不能两两配对嘛……
我瞄了一眼题解
Std代码不对应,请忽略!

#include <cstdio> #include <algorithm> #include <vector> #define FOR(i, l, r) for(int i = l; i <= r; ++i) #define mp(x, y) make_pair(x, y) using namespace std; typedef long long ll; const int N = 200010; const ll inf = 1e15; struct edge{int u, v, lim;} e[N]; bool operator < (edge a, edge b) {return a.lim < b.lim;} vector<pair<int, ll> > ans; int n, m, Q, x; int fa[N], a[N], og[N]; ll up[N]; int find(int x) {return x == fa[x] ? x : fa[x] = find(fa[x]);} int main() { freopen("poisoning.in" , "r" , stdin); freopen("poisoning.out" , "w", stdout); scanf("%d%d%d", &n, &m, &Q); FOR(i, 1, n) { scanf("%d", a + i); ans.push_back(mp(0, a[i])); } FOR(i, 1, m) scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].lim); FOR(i, 1, n) fa[i] = i, up[i] = a[i], og[i] = 0; sort(e + 1, e + m + 1); FOR(i, 1, m) { int p = find(e[i].u), q = find(e[i].v); if (p == q) continue; og[q] = min(max((ll)og[p], e[i].lim - up[p]), max((ll)og[q], e[i].lim - up[q])); up[q] += up[p]; fa[p] = q; ans.push_back(mp(og[q], up[q])); } sort(ans.begin(), ans.end()); for(int i = 1; i < ans.size(); ++i) ans[i].second = max(ans[i].second, ans[i - 1].second); while (Q--) { scanf("%d", &x); printf("%d ", (--upper_bound(ans.begin(), ans.end(), make_pair(x, inf))) -> second + x); } return 0; }
???
又用了STL?
看来std是个高手呀!
for循环都懒得写了,哼╭(╯^╰)╮
回到本源
若原树存在完美匹配
如果 B 能通过切边,把所有匹配都分割开来,B 赢,
否则 A 赢 充分性显然 A 选一个点,B 选与他匹配的一个点就好了
必要性: 如果不能完全分隔开,必然留下一个连通块,K = 0 , n > 2
由结论 2,A 赢
所以,贪心看下树有没有完美匹配就好了
时间复杂度 O(n)
5000 是用来吓唬人的?!?!?!
OK!
