中国剩余定理(CRT)
怎么说
我听了三遍才懂emmm
再次感谢wjh dalao倾情讲解加手写演绎

这样一个同余方程组,要求一个x
使x满足以上所有条件,其中m1——mk互素
将m1到mk累乘
构造M = m1 * m2 * ... * mk
因为m互素,所以M为m的lcm
这样易得
M / mi ≡ 0 (mod mj) (i != j)
利用exgcd求出M / mi的逆元,使得
M / mi * ti ≡ 1 (mod mi)
(不会exgcd指路这里——>同余方程,exgcd
(不会逆元指路这里——>乘法逆元
我们知道在mod m意义下,两边同乘不干扰
所以将上式两边同乘ai
ai * M / mi * ti ≡ ai (mod mi)
我们发现,这个式子的右边是原方程组的右边
那么左边就自然是x的值了
而x需要满足所有的同余方程
那么
![]()
特别的 (x % M + M) % M是最小整数解
两道模版题
放一段crt的核心代码
ll quickmul(ll n,ll k){ ll ans = 0; while(k > 0){ if(k & 1) ans = (ans + n) % M; n = (n + n) % M; k >>= 1; } return ans % M; }//猜数字中需要用到快速乘 void exgcd(ll a,ll b,ll &x,ll &y){ if(b == 0){ x = 1; y = 0; return ; } exgcd(b,a % b,x,y); ll tmp = x; x = y; y = tmp - a / b * y; }//exgcd int main() { int k; M = 1; scanf("%d",&k); for(int i = 1; i <= k; i++) scanf("%lld",&a[i]); for(int i = 1; i <= k; i++) { scanf("%lld",&m[i]); M *= m[i]; } ll ans = 0; for(int i = 1; i <= k; i++) a[i] = (a[i] % m[i] + m[i]) % m[I];//先将a处理一下 for(int i = 1; i <= k; i++){ ll x,y; exgcd(M / m[i],m[i],x,y);//求出ti,即为x x = (x % m[i] + m[i]) % m[i]; ans = (ans + quickmul(quickmul(M / m[i],x),a[i])) % M; //多膜 } printf("%lld",(ans % M + M) % M);//多膜 return 0; }
扩展中国剩余定理(EXCRT)
看了一篇博客就看懂了
但是做题的话
想起来会比较难
写一下博客加深印象emmm
首先还是一个同余方程组
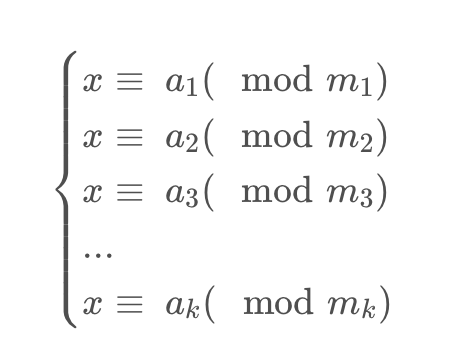
不过这次m1——mk啥关系没有【滑稽
我们从只有两组方程开始考虑
可以得到:
x = a1 + k1 ∗ m1
x = a2 + k2 ∗ m2
所以
a1 + k1 ∗ m1 = a2 + k2 ∗ m2
k2∗m2−k1∗m1=a1−a2
有没有一点眼熟?
是不是很像
a * x + b * y = c
这样我们设
c = a1 - a2
这样我们需要c是gcd(m1,m2)的倍数才能求出解
如果不是倍数无解
如果是的话,就可以用exgcd求出 k2 * m2 + k1 * m1 = gcd(m1,m2)中的k1的值
c为gcd(m1,m2)的倍数
则 k1 = k1 * c / gcd(m1,m2)
题解说最好 k1 % 一下 m2怕爆long long
这样我们可以反推出来x
x = a1 - k1 * m1
可以得到通解是:x = x + k * lcm(m1,m2)
将这个方程转化一下,可以得到新的同余方程
x = x0 (mod lcm(m1,m2) )
于是我们把两个方程变成了一个
以此类推
最终可以得到结果
这是一道版子题
但是它保证数据都有解
看一下代码
#include<cstdio> #define sev en using namespace std; #define ll long long #define N 100010 ll a[N],m[N],M; ll ans; ll quickmul(ll a,ll k,ll z){ ll res = 0; while(k){ if(k & 1) res = (res + a) % z; a = (a + a) % z; k >>= 1; } return res; }//快速乘了一下 ll exgcd(ll a,ll b,ll &x,ll &y){ if(b == 0){ x = 1; y = 0; return a; } ll as = exgcd(b,a % b,x,y); ll tmp = x; x = y; y = tmp - a / b * y; return as; }//exgcd int main(){ int n; scanf("%d",&n); for(int i = 1;i <= n;i++) scanf("%lld%lld",&m[i],&a[i]);//这里的输入我给反过来了 ans = a[1],M = m[1];//首先把第一组同余方程的值赋上 for(int i = 2;i <= n;i++){ ll x,y; ll s = (a[i] - ans % m[i] + m[i]) % m[i];//这里相当于a1 - a2 = c ll gcd = exgcd(M,m[i],x,y);//求gcd x = quickmul(x,s / gcd,m[i]);//x为k1,k1 * c / gcd ans += x * M;//ans加上求出的值 M *= m[i] / gcd;//把两个同余方程的模数合并 ans = (ans % M + M) % M;//最小整数解 } printf("%lld",(ans % M + M) % M); return 0; }
需要注意的是,如果不保证数据一定有解
就把excrt的部分写在外面
返回ans再输出
中途判断 s 是否是 gcd 的倍数
不是的话直接返回-1或看题目要求
然后就没有然后啦
写完了感觉还不错emmmm(自我欣赏一下www
理解的海星,jio的最近效率蛮高的2333