题目如下:
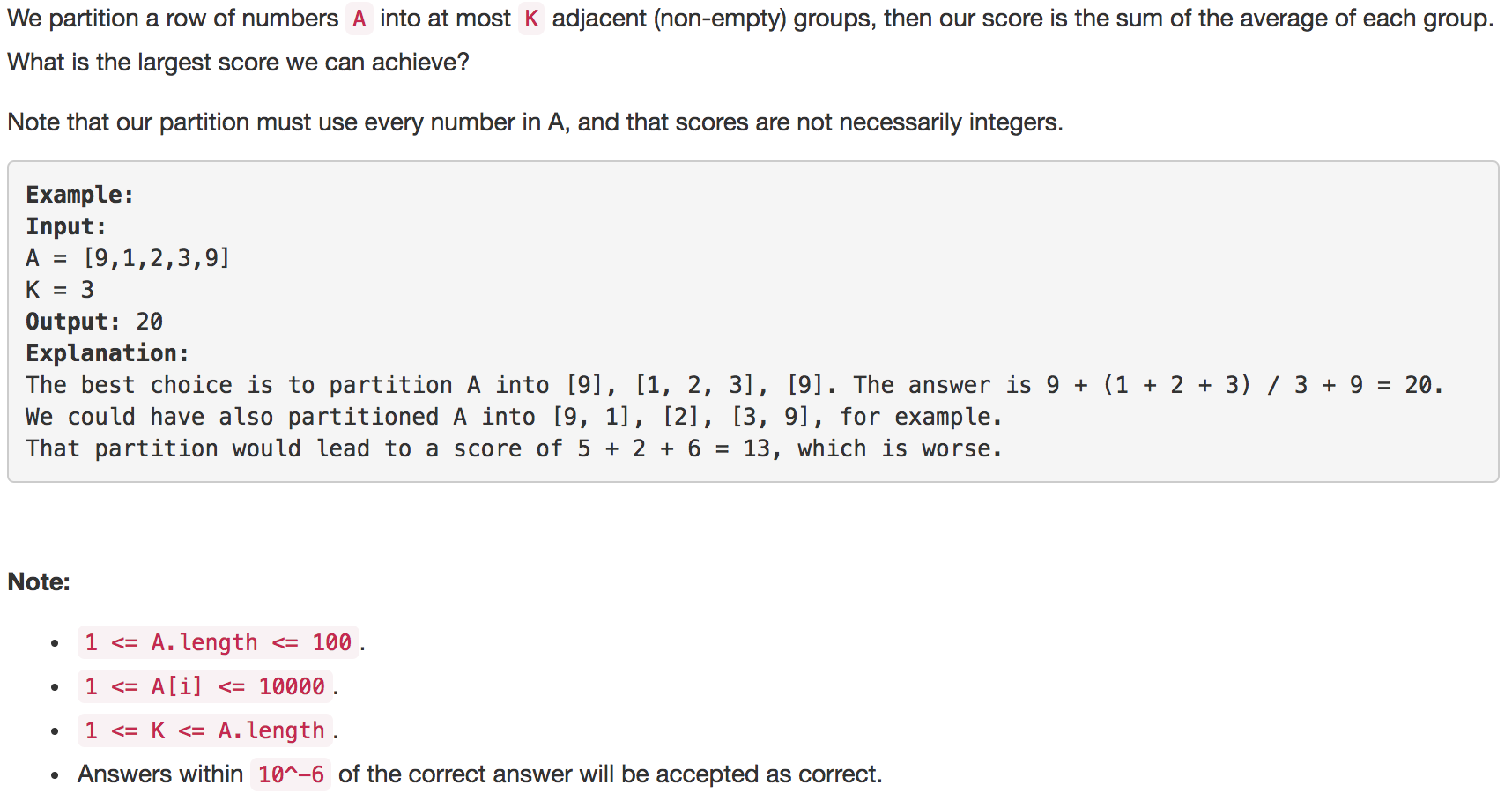
解题思路:求最值的题目优先考虑是否可以用动态规划。记dp[i][j]表示在数组A的第j个元素后面加上第i+1 (i从0开始计数)个分隔符后可以得到的最大平均值,那么可以得到递归关系式: dp[i][j] = max(dp[i][j],dp[i-1][k]+float(sum(A[k+1:j+1]))/float(j-k)) 。
代码如下:
class Solution(object): def largestSumOfAverages(self, A, K): """ :type A: List[int] :type K: int :rtype: float """ tl = [0] * len(A) dp = [] for i in range(K): dp.append(tl[:]) count = 0 for i in range(len(dp)): for j in range(len(dp[i])-K+i+1): count += A[j] if i == 0: dp[i][j] = float(count)/float(j+1) continue for k in range(j): #print k,j,sum(A[k:j]) dp[i][j] = max(dp[i][j],dp[i-1][k]+float(sum(A[k+1:j+1]))/float(j-k)) return dp[-1][-1]