题目如下:
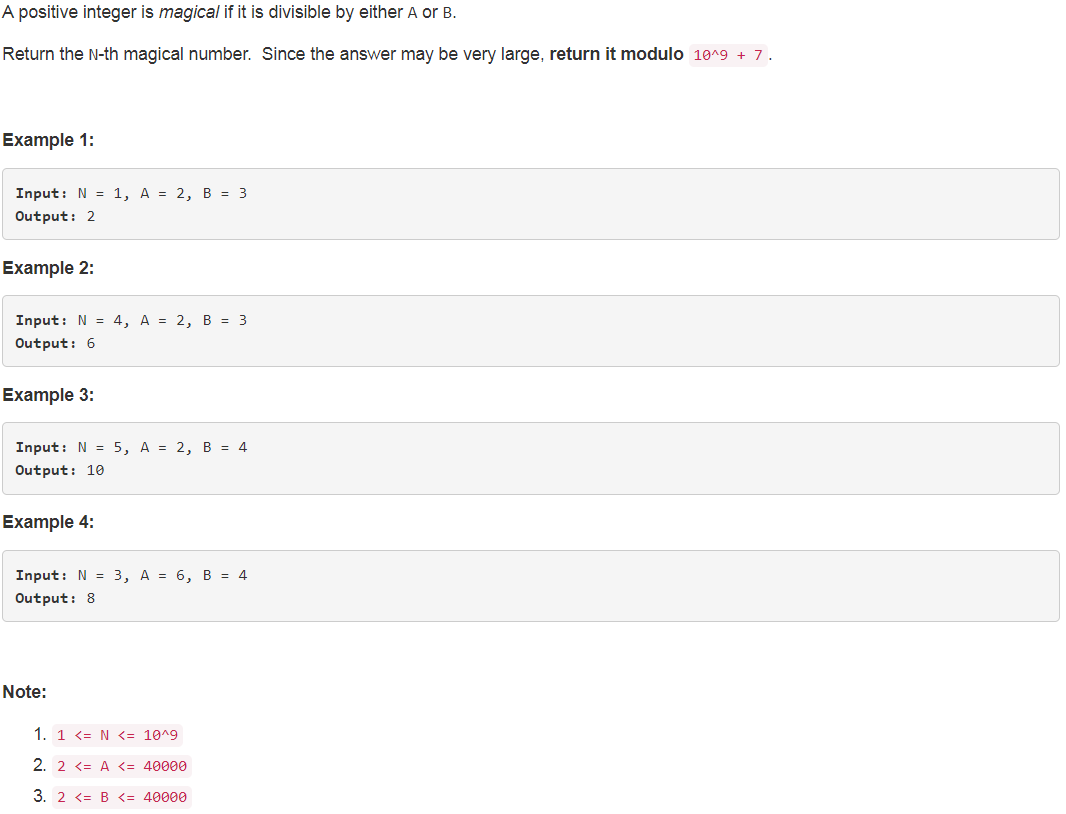
解题思路:本题求的是第N个Magical Number,我们可以很轻松的知道这个数的取值范围 [min(A,B), N*max(A,B)]。对于知道上下界求具体数字的题目,可以考虑用二分查找。这样题目就从找出第N个Magical Number变成判断一个数是否是第N个Magical Number。假设n是其中一个Magical Number,显然n满足 n % A == 0 或者 n % B == 0。对于A来说,从A到n之间有n/A个Magical Number,而对B来说是n/B个Magical Number。但是n却并不是第(n/A + n/B)个Magical Number,因为这两者之间会有满足A * i == B * j数字出现,这样会造成重复,这样的数字有多少个呢?和A与B的最小公倍数有关,有n/LCM(A,B)个。
代码如下:
def gcd(m,n): if not n: return m else: return gcd(n, m%n) def lcm(m, n): if m*n == 0: return 0 return int(m*n/gcd(m, n)) class Solution(object): def getMagical(self,N,LCM,v1,v2): low = 0 high = N flag = False while low <= high: mid = (low + high) / 2 count = mid + (mid * v1) / v2 - (mid * v1) / LCM if count == N: flag = True break elif count < N: low = mid + 1 else: high = mid - 1 return flag,mid * v1 def nthMagicalNumber(self, N, A, B): LCM = lcm(A, B) minv, maxv = min(A, B), max(A, B) flag,res = self.getMagical(N,LCM,minv,maxv) if flag: return res % (pow(10,9) + 7) #flag = False表示第n个magical number不是minv的倍数,用maxv再找一遍 return self.getMagical(N, LCM, maxv, minv)[1] % (pow(10,9) + 7)