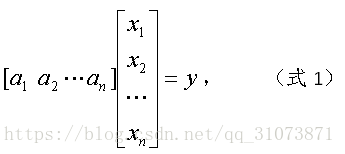https://blog.csdn.net/qq_31073871/article/details/81067301
已知变量X和Y为线性关系(这里XY均为nx1的列向量),为了得知X和Y到底具有怎样的线性关系(也即求解X的系数),如果这是一个工程问题,我们解决这一问题的方法就是对X和Y进行采样,获得很多组样本,然后就能求解出系数了,按照线代的理论,系数矩阵为nxn方阵,且秩为n时,方程具有唯一解,如果采样点过多,也即方程的数目多于未知数的数目,则方程组无解,这时只能求出一个近似解,以不同的目的获得的近似解是不同的,如果为了使方程左右两边的误差的平方和最小,而获得的近似解,就是最小二乘解(所谓“二乘”,就是“平方”的意思,最小二乘就是最小平方和)。这个问题的证明在研究生的矩阵分析引论数学课上学过,现在也忘光了,只记得结论表达式了。
例子:假设变量y是n个变量xi的线性组合,求系数。
设方程为AX=y,也即
为了计算出系数a1、a2、···an的值,我们至少需要n次X、Y的采样值,形如:

这样就能求解出系数a1、a2、···an的值了,如果采样样本不止n个,而是多于n个,也不要紧,虽然会会造成方程组无解,但是可以求出最小二乘解。
把方程组写成矩阵形式为:
XA=Y (式2)
至此,就求出了所有的系数ai
-----------------------------------------------------后记---------------------------------------------------------------------
又翻了电子版课本,把最小二乘的证明过程也贴上来:
证明过程在《矩阵分析引论》第30页。证明过程需要用到子空间的概念,这一概念的定义在第6页。


最后简单整理一下证明过程:

————————————————
版权声明:本文为CSDN博主「qq_610642」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_31073871/article/details/81067301
参考1:https://blog.csdn.net/lsh_2013/article/details/46697625