NOI题库 1768最大子矩阵 题解

NOI题库 1768最大子矩阵  题解

 

 

总时间限制: 1000ms 内存限制: 65536kB

 

描述

 

已知矩阵的大小定义为矩阵中所有元素的和。给定一个矩阵，你的任务是找到最大的非空(大小至少是1 * 1)子矩阵。

比如，如下4 * 4的矩阵

 

0 -2 -7 0

9 2 -6 2

-4 1 -4 1

-1 8 0 -2

 

的最大子矩阵是

 

9 2

-4 1

-1 8

 

这个子矩阵的大小是15。

 

输入

 

输入是一个N * N的矩阵。输入的第一行给出N (0 < N <= 100)。再后面的若干行中，依次（首先从左到右给出第一行的N个整数，再从左到右给出第二行的N个整数……）给出矩阵中的N2个整数，整数之间由空白字符分隔（空格或者空行）。已知矩阵中整数的范围都在[-127, 127]。

 

输出

 

输出最大子矩阵的大小。

 

样例输入

4

0 -2 -7 0

9 2 -6 2

-4 1 -4 1

-1 8 0 -2

 

样例输出

15

 

 

———————————————————————————————————————

 

 

分析

最初看到这道题时，我完全不知道怎么DP，只能想到暴力算法，这道题的最暴力想法就是枚举，但是这个想法的时间复杂度达到O(N^4),当数据较大时无法承受，经大神指点得知，可以使用动态规划解决这个问题。那么，怎么用动态规划呢？

最初学DP时，有一个求最大子段和的问题，可以通过DP解决，最大子矩阵只是最大子段和在二维中的扩展，为了能继续使用这种方法，我们需要将这个矩阵降维处理，降维操作如下图：

 

这是样例中4*4的矩阵，红色框中是进行降维操作的矩阵

 

 

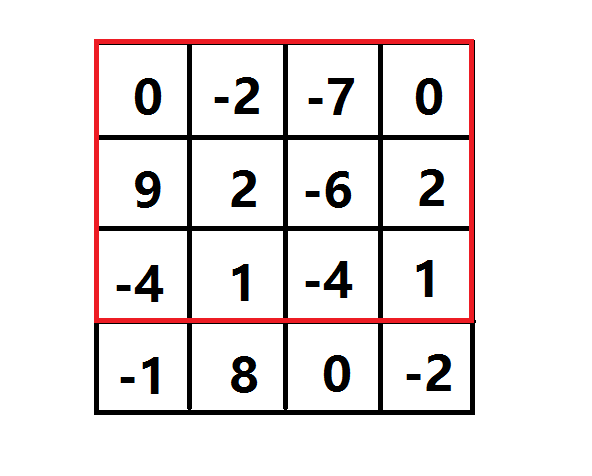
 降维的操作很简单，只需要将同一列的加和，就能得到目标序列，我们可以使用前缀和思想来优化这个操作。

 

通过这个操作可以将二维矩阵降维，随后就可以用区间DP的方法解决这个最大子矩阵的问题。

 

代码如下：

 

#include "cstdio"
#include "cstring"
#include "algorithm"
#include "cmath"
using namespace std ;

int gmax( int a , int b)//求最大值
{
    return a > b ? a : b ;
}

int best[110], temp[110];

int tmp[110][110], pr[110][110];

void Init ( int n )
{
    for( int i = 1 ; i <= n ; ++i )pr[1][i] = tmp[1][i] ;//pr[]数组用前缀和思想
    for(int i = 2 ; i <= n ; ++i )
        for (int j = 1 ; j <= n ; ++j )
            pr[i][j] = pr[i - 1][j] + tmp[i][j] ;//计算前缀和
    return ;
}

int solve ( int *a , int N)
{

    memset ( best , 0 , sizeof(best));//best数组表示以i为结尾的最大子序列和
    int ans = -2147483647 ;
    for ( int i = 1 ; i <= N ; ++i)
    {
        if ( best[i - 1] + a[i] > a[i])
        {
            best[i] = best[i - 1] + a[i] ;//DP方程
        }
        else
        {
            best[i] = a[i] ;//DP方程
        }
    }
    for ( int i = 1 ; i <= N ; ++i )ans = gmax( ans , best[i]);//求出best数组中的最大值，即最大子序列和
    return ans ;
}

int main ( )
{
    int ans = -2147483647 , n;
    scanf("%d", &n);
    for(int i = 1 ; i <= n ; ++i )
    {
        for (int j = 1 ; j <= n ; ++j )
        {
            scanf("%d", &tmp[i][j]);
        }
    }
    Init ( n );//预处理
    for ( int i = 1 ; i <= n ; ++i)
    {
        for ( int j = i ; j <= n ; ++j )
        {
            memset( temp , 0 , sizeof(temp));
            for ( int k = 1 ; k <= n ; ++k )
            {
                temp[k] = pr[j][k] - pr[i - 1][k];//temp数组是降维后的数组
            }
            ans = gmax(solve ( temp , n) , ans );//求出最大值
        }
    }
    printf("%d
", ans);
    return 0 ;
}

——————————————————————————————————————

（完）