八大排序算法的时间、空间复杂度和稳定性
❀八大排序算法对应的文章:
《八大排序算法之直接插入排序(教你用生活的想象,读懂插入算法) 》
《八大排序算法~快速排序 》
《八大排序算法~堆排序 》
一,各个算法的情况与分析:
时间复杂度~一般咱就考虑平均情况就行,除非要求对时间特别苛刻才考最差情况~八大算法里就那个希尔排序跟快排时间复杂度最坏跟平均不同
1、直接插入排序 的时间和空间效率:
✪ 时间复杂度:O(n2),空间复杂度:O(1); ~因为在空间上没有利用什么辅助空间~稳定
2、希尔排序 的时间跟空间效率:
✪ 时间复杂度:大约O(n1.3),空间复杂度:O(1); ~因为在空间上没有利用什么辅助空间~不稳定
不稳定的原因~假设有两个相同的数字在两个不同的子序列里边,如果每个子序列把小数扔前大数扔后,可能导致两个位置发生先后改变。
✿ 希尔排序注意点:不宜在链式结构上进行实现~因为分割的间隔d的值导致每个子序列的元素之间出现间隔,使用数组有下标可以快速找到哈!
3、冒泡排序 的时间跟空间效率:
✪ 时间复杂度:O(n2),空间复杂度:O(1); ~因为在空间上没有利用什么辅助空间~稳定
4、快速排序 的时间跟空间效率:
✪ 时间复杂度:O(nlog2n),空间复杂度:O(log2n); ~ ~不稳定
■为什么时间是O(nlog2n)呢? ---递归算法耗费时间:O(log2n)
---其余数跟中心点进行比较耗费时间: O(n)
■为什么空间是O(log2n)呢?----快速排序不是原地排序---递归需要用到栈,而栈的长度取决于调用的深度,平均情况是 O(log2n),最差情况是O(n)。
不稳定的原因~假设有两个相同的数字,取第一个数为中心点,当比较后会出现low=high的那个位置,导致第一个数放到low=high位置上导致两个数前后顺序发生改变。
5、简单(直接)选择排序 的时间跟空间效率:
✪ 时间复杂度:O(n2),空间复杂度:O(1); ~因为在空间上没有利用什么辅助空间~不稳定。
不稳定的原因~直接选择排序~擂台法【找小,从小到大排序】,假设有两个相同的数字,当第一个数比擂台上的数还小,则替换掉擂台上的数,然后在第二个数的后边又出现了其他比擂台的数替换掉擂台上的数,导致两个数前后顺序发生改变。
6、堆排序 的时间跟空间效率:
✪ 时间复杂度:O(nlog2n),空间复杂度:O(1); ~~因为在空间上没有利用什么辅助空间~不稳定
■为什么时间是O(nlog2n)呢? ---递归算法耗费时间:O(log2n)
---最后一个元素放到根结点后,其余元素位置需要遍历调整: O(n)。
不稳定的原因~调成成大根堆(或小根堆)时数据的调整导致相同的两个数据先后位置发生改变。
✿ 堆排序注意点:不适合待排记录个数较少的情况,对于n较大的文件还是很有效的。
7、归并排序 的时间跟空间效率:
✪ 时间复杂度:O(nlog2n),空间复杂度:O(n); ~~稳定
■为什么时间是O(nlog2n)呢? ---递归算法耗费时间:O(log2n)趟
---所有元素都需要进行归并,每一趟都要合并n个元素: O(n)
8,基数排序(也叫桶排序)的时间跟空间效率:
✪ 时间复杂度:O(k*(n + m)),空间复杂度:O(n+m); ~稳定
●为什么时间是O(k*(n + m))呢?
■ k 是关键字的位数的个数,例如待排数据中的最大一个数有三位数(个十百),则k=3;
■ n 是要分配n个数,m是要收集的m个数(m就是桶数,从桶中收集数据);
●为什么空间是O(n + m)呢?
■ 辅助空间是有m个桶,每个桶的深度是n;
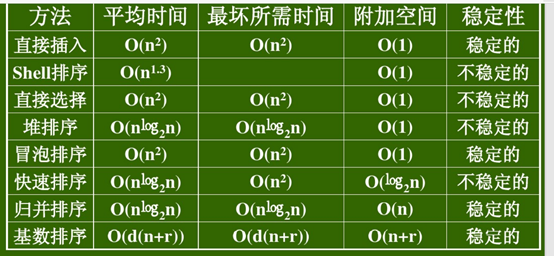
二,总结八大算法的时间、空间效率、稳定性:
引自:《数据结构c语言版严蔚敏PPT.pdf ~
https://wenku.baidu.com/view/9e73cb8b69dc5022aaea00c1.html》
三,使用建议:
3-1,按时间性能考虑(平均时间性能):
■ 时间复杂度O(nlog2n):快排、堆排、归并~特点都用到了递归~快排最优
■ 时间复杂度O(n):桶排
■ 时间复杂度O(n2):冒泡、直接选择、直接插入~特点外层循环进行趟数,内循环比较个数~直接插入最优
✿ 注意:当待排记录序列按关键字顺序有序时,直接插入和冒泡排序都能到到的时间复杂度为O(n);而此时对快排是最不好的情况,导致其时间复杂度退化为O(n2);
3-2,按空间性能(辅助空间)考虑:
■ 空间复杂度O(1):冒泡、简单选择、直接插入、希尔、堆排~特点是就地排序
■ 空间复杂度O(log2n):快排~因为栈所需辅助空间
■ 空间复杂度O(n):归并、桶排
3-3,按稳定性考虑(稳定性~两个相同的数据因排序导致原先的先后顺序发生改变):
■ 八大排序不稳定算法: 希尔、直接选择、快排、堆排
■ 其中最不稳定算法:快排、堆排