Problem 5 素数筛法+并查集

$des$

给定一个长度为 $n$ 的正整数序列 ${a_i }$。
将 ${1,2,...,n}$ 划分成两个非空集合 $S、T$，使得 $gcd(prod_{i in S} a_i,
prod_{i in T} a_i) = 1$
求划分方案数，对 $10^9 + 7$ 取模。

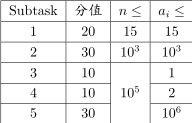
$sol$

对于两个数 $a, b$ 必须处于同一个集合，当其含有相同因子。
这样的话，将含有相同因子的数用并查集维护。
最后统计所有的 $n$ 个数被分成了 $x$ 个集合
答案就是 $2 ^ n - 2$，$1$ 需要特判

#include <bits/stdc++.h>

using namespace std;

#define gc getchar()
inline int read() {
    int x = 0; char c = gc;
    while(c < '0' || c > '9') c = gc;
    while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = gc;
    return x;
}

#define Rep(i, a, b) for(int i = a; i <= b; i ++)
#define LL long long

const int N = 1e5 + 10, To = 1e6;

bool Check[To + 10];
int tot, prime[To];

int fa[To + 10];
int n;
int A[N];
bool Use[To];

void Get() {
    Rep(i, 2, To) {
        if(!Check[i]) prime[++ tot] = i;
        Rep(j, 1, tot) {
            if(prime[j] * i > To) break;
            Check[i * prime[j]] = 1;
            if(i % prime[j] == 0) break;
        }
    }
}

int Get(int x) {
    return fa[x] == x ? x : fa[x] = Get(fa[x]);
}

const int Mod = 1e9 + 7;

LL Ksm(LL a, LL b) {
    LL ret = 1;
    while(b) {
        if(b & 1) ret = ret * a % Mod;
        a = a * a % Mod;
        b >>= 1;
    }
    return ret;
}

int vis[To];

int main() {
    Get();
    for(int T = read(); T; T --) {
        n = read();
        int js = 0;
        memset(Use, 0, sizeof Use);
        int Max = 0;
        Rep(i, 1, n) A[i] = read(), Use[A[i]] = 1, Max = max(Max, A[i]), js += (A[i] == 1);
        Rep(i, 1, To) fa[i] = i;
        Rep(i, 1, tot) {
            if(prime[i] > Max) break;
            for(int j = 1; j * prime[i] <= Max; j ++) {
                int num = j * prime[i];
                if(Use[num]) {
                    int fa1 = Get(num), fa2 = Get(prime[i]);
                    if(fa1 != fa2) fa[fa1] = fa2;
                }
            }
        }
        LL up = 0;
        Rep(i, 1, n) {
            int f = Get(A[i]);
            if(vis[f] != T) vis[f] = T, up ++;
        }
        if(js > 1) up += (js - 1);
        LL ans = Ksm(2, up);
        ans -= 2;
        if(ans < 0) ans += Mod;
        cout << ans << "
";
    }
    
    return 0;
}