C# CAD 凹凸点识别最大轮廓

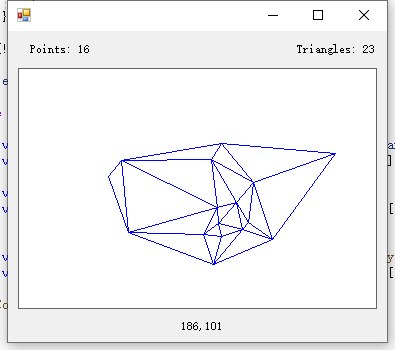
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace Beaver.Unfold.Core
{
    /// <summary>
    /// 最大凹凸面
    /// </summary>
    public class Csharp_Delauney
    {
        // ---------------------------------------------------------------
        // ---------------------------------------------------------------
        // ---------------------------------------------------------------
        //Points (Vertices)
        public struct dVertex
        {
            public double x;
            public double y;
            public double z;
        }

        //Created Triangles, vv# are the vertex pointers
        public struct dTriangle
        {
            public int vv0;
            public int vv1;
            public int vv2;
        }

        //Set these as applicable
        public int MaxVertices = 1500;
        public int MaxTriangles = 3000;
        public dVertex[] Vertex;
        public dTriangle[] Triangle;
        public int HowMany = 0;

        int tPoints; //Variable for total number of points (vertices)

        public Csharp_Delauney()
        {
            // ------------------------------------------------------------------------------------
            //Our points
            Vertex = new dVertex[MaxVertices];
            //Our Created Triangles
            Triangle = new dTriangle[MaxTriangles];
            //Initiate total points to 1, using base 0 causes problems in the functions
            tPoints = 1;

            // ------------------------------------------------------------------------------------
            //
            // TODO: Add any constructor code after InitializeComponent call
            //
        }

        public int Triangulate(ref int nvert)
        {
            // Takes as input NVERT vertices in arrays Vertex()
            // Returned is a list of NTRI triangular faces in the array
            // Triangle(). These triangles are arranged in clockwise order.
            bool[] Complete = new bool[MaxTriangles];
            int[,] Edges = new int[3, MaxTriangles * 3];

            int Nedge;

            // For Super Triangle
            double xmin;
            double xmax;
            double ymin;
            double ymax;
            double xmid;
            double ymid;
            double dx;
            double dy;
            double dmax;

            // General Variables
            int i;
            int j;
            int k;
            int ntri;
            bool inc;

            double xc;
            xc = 0;
            double yc;
            yc = 0;
            double r;
            r = 0;

            // Find the maximum and minimum vertex bounds.
            // This is to allow calculation of the bounding triangle
            xmin = Vertex[1].x;
            ymin = Vertex[1].y;
            xmax = xmin;
            ymax = ymin;
            for (i = 2; i <= nvert; i++)
            {
                if (Vertex[i].x < xmin)
                {
                    xmin = Vertex[i].x;
                }
                if (Vertex[i].x > xmax)
                {
                    xmax = Vertex[i].x;
                }
                if (Vertex[i].y < ymin)
                {
                    ymin = Vertex[i].y;
                }
                if (Vertex[i].y > ymax)
                {
                    ymax = Vertex[i].y;
                }
            }

            dx = xmax - xmin;
            dy = ymax - ymin;
            if (dx > dy)
            {
                dmax = dx;
            }
            else
            {
                dmax = dy;
            }

            xmid = (xmax + xmin) / 2;
            ymid = (ymax + ymin) / 2;

            // Set up the supertriangle
            // This is a triangle which encompasses all the sample points.
            // The supertriangle coordinates are added to the end of the
            // vertex list. The supertriangle is the first triangle in
            // the triangle list.
            Vertex[nvert + 1].x = (int)(xmid - 2 * dmax);
            Vertex[nvert + 1].y = (int)(ymid - dmax);
            Vertex[nvert + 2].x = (int)xmid;
            Vertex[nvert + 2].y = (int)(ymid + 2 * dmax);
            Vertex[nvert + 3].x = (int)(xmid + 2 * dmax);
            Vertex[nvert + 3].y = (int)(ymid - dmax);
            Triangle[1].vv0 = nvert + 1;
            Triangle[1].vv1 = nvert + 2;
            Triangle[1].vv2 = nvert + 3;
            Complete[1] = false;
            ntri = 1;
            // Include each point one at a time into the existing mesh
            for (i = 1; i <= nvert; i++)
            {

                Nedge = 0;
                // Set up the edge buffer.
                // If the point (Vertex(i).x,Vertex(i).y) lies inside the circumcircle then the
                // three edges of that triangle are added to the edge buffer.
                j = 0;
                do
                {
                    j = j + 1;
                    if (Complete[j] != true)
                    {
                        inc = InCircle(ref Vertex[i].x, ref Vertex[i].y, ref Vertex[Triangle[j].vv0].x, ref Vertex[Triangle[j].vv0].y, ref Vertex[Triangle[j].vv1].x, ref Vertex[Triangle[j].vv1].y, ref Vertex[Triangle[j].vv2].x, ref Vertex[Triangle[j].vv2].y, ref xc, ref yc, ref r);
                        // Include this if points are sorted by X
                        // If (xc + r) < Vertex(i).x Then
                        // complete(j) = True
                        // Else
                        if (inc)
                        {
                            Edges[1, Nedge + 1] = Triangle[j].vv0;
                            Edges[2, Nedge + 1] = Triangle[j].vv1;
                            Edges[1, Nedge + 2] = Triangle[j].vv1;
                            Edges[2, Nedge + 2] = Triangle[j].vv2;
                            Edges[1, Nedge + 3] = Triangle[j].vv2;
                            Edges[2, Nedge + 3] = Triangle[j].vv0;
                            Nedge = Nedge + 3;
                            Triangle[j].vv0 = Triangle[ntri].vv0;
                            Triangle[j].vv1 = Triangle[ntri].vv1;
                            Triangle[j].vv2 = Triangle[ntri].vv2;
                            Complete[j] = Complete[ntri];
                            j = j - 1;
                            ntri = ntri - 1;
                        }
                    }
                } while (j < ntri);

                // Tag multiple edges
                // Note: if all triangles are specified anticlockwise then all
                // interior edges are opposite pointing in direction.
                for (j = 1; j <= Nedge - 1; j++)
                {
                    if (Edges[1, j] != 0 && Edges[2, j] != 0)
                    {
                        for (k = j + 1; k <= Nedge; k++)
                        {
                            if (Edges[1, k] != 0 && Edges[2, k] != 0)
                            {
                                if (Edges[1, j] == Edges[2, k])
                                {
                                    if (Edges[2, j] == Edges[1, k])
                                    {
                                        Edges[1, j] = 0;
                                        Edges[2, j] = 0;
                                        Edges[1, k] = 0;
                                        Edges[2, k] = 0;
                                    }
                                }
                            }
                        }
                    }
                }
                // Form new triangles for the current point
                // Skipping over any tagged edges.
                // All edges are arranged in clockwise order.
                for (j = 1; j <= Nedge; j++)
                {
                    if (Edges[1, j] != 0 && Edges[2, j] != 0)
                    {
                        ntri = ntri + 1;
                        Triangle[ntri].vv0 = Edges[1, j];
                        Triangle[ntri].vv1 = Edges[2, j];
                        Triangle[ntri].vv2 = i;
                        Complete[ntri] = false;
                    }
                }
            }
            // Remove triangles with supertriangle vertices
            // These are triangles which have a vertex number greater than NVERT
            i = 0;
            do
            {
                i = i + 1;
                if (Triangle[i].vv0 > nvert || Triangle[i].vv1 > nvert || Triangle[i].vv2 > nvert)
                {
                    Triangle[i].vv0 = Triangle[ntri].vv0;
                    Triangle[i].vv1 = Triangle[ntri].vv1;
                    Triangle[i].vv2 = Triangle[ntri].vv2;
                    i = i - 1;
                    ntri = ntri - 1;
                }
            } while (i < ntri);

            return ntri;

        }

        private bool InCircle(ref double xp, ref double yp, ref double x1, ref double y1, ref double x2, ref double y2, ref double x3, ref double y3, ref double xc, ref double yc, ref double r)
        {
            //Return TRUE if the point (xp,yp) lies inside the circumcircle
            //made up by points (x1,y1) (x2,y2) (x3,y3)
            //The circumcircle centre is returned in (xc,yc) and the radius r
            //NOTE: A point on the edge is inside the circumcircle
            bool TheResult;

            double eps;
            double m1;
            double m2;
            double mx1;
            double mx2;
            double my1;
            double my2;
            double dx;
            double dy;
            double rsqr;
            double drsqr;

            TheResult = false;
            eps = 0.000001;

            if (System.Math.Abs(y1 - y2) < eps && System.Math.Abs(y2 - y3) < eps)
            {
                //MessageBox.Show("INCIRCUM - F - Points are coincident !!");
                TheResult = false;
                return TheResult;
            }


            if (System.Math.Abs(y2 - y1) < eps)
            {
                m2 = (double)-(x3 - x2) / (y3 - y2);
                mx2 = (double)(x2 + x3) / 2;
                my2 = (double)(y2 + y3) / 2;
                xc = (x2 + x1) / 2;
                yc = m2 * (xc - mx2) + my2;
            }
            else if (System.Math.Abs(y3 - y2) < eps)
            {
                m1 = (double)-(x2 - x1) / (y2 - y1);
                mx1 = (double)(x1 + x2) / 2;
                my1 = (double)(y1 + y2) / 2;
                xc = (x3 + x2) / 2;
                yc = m1 * (xc - mx1) + my1;
            }
            else
            {
                m1 = (double)-(x2 - x1) / (y2 - y1);
                m2 = (double)-(x3 - x2) / (y3 - y2);
                mx1 = (double)(x1 + x2) / 2;
                mx2 = (double)(x2 + x3) / 2;
                my1 = (double)(y1 + y2) / 2;
                my2 = (double)(y2 + y3) / 2;
                xc = (m1 * mx1 - m2 * mx2 + my2 - my1) / (m1 - m2);
                yc = m1 * (xc - mx1) + my1;
            }

            dx = x2 - xc;
            dy = y2 - yc;
            rsqr = dx * dx + dy * dy;
            r = System.Math.Sqrt(rsqr);
            dx = xp - xc;
            dy = yp - yc;
            drsqr = dx * dx + dy * dy;

            if (drsqr <= rsqr)
            {
                TheResult = true;

            }
            return TheResult;

        }

        public dVertex[] AddPoint(double x , double y)
        {
            int i;

            // variable to hold how many triangles are created by the triangulate function
            HowMany = 0;

            // Set Vertex coordinates where you clicked the pic box
            Vertex[tPoints].x = x;
            Vertex[tPoints].y = y;

            // Perform Triangulation Function if there are more than 2 points
            if (tPoints > 2)
            // Clear the Picture Box
            {
                // Returns number of triangles created.
                HowMany = Triangulate(ref tPoints);
            }
            else
            {
                // Draw a circle where you clicked so it does something
                // g.DrawRectangle(myPen, Vertex(tPoints).x, Vertex(tPoints).y, 14, 14)
                //g.DrawEllipse(myPen, Vertex[tPoints].x, Vertex[tPoints].y, 4, 4);
            }



            // Display the total points and total triangles
            //label4.Text = "Points: " + tPoints;
            //label5.Text = "Triangles: " + HowMany;

            // Increment the total number of points
            tPoints = tPoints + 1;

            // Draw the created triangles
            for (i = 1; i <= HowMany; i++)
            {
                //g.DrawLine(myPen, Vertex[Triangle[i].vv0].x, Vertex[Triangle[i].vv0].y, Vertex[Triangle[i].vv1].x, Vertex[Triangle[i].vv1].y);
                //g.DrawLine(myPen, Vertex[Triangle[i].vv1].x, Vertex[Triangle[i].vv1].y, Vertex[Triangle[i].vv2].x, Vertex[Triangle[i].vv2].y);
                //g.DrawLine(myPen, Vertex[Triangle[i].vv0].x, Vertex[Triangle[i].vv0].y, Vertex[Triangle[i].vv2].x, Vertex[Triangle[i].vv2].y);
            }
            return Vertex;

        }

        public dVertex[] GetDVertices()
        {
            return Vertex;
        }
        public dTriangle[] GetDTriangles()
        {
            return Triangle;
        }
    }
}
-----------------------------

调用
Csharp_Delauney csharp_Delauney = new Csharp_Delauney();
                    foreach (var entity in pionts)
                    {
                        if (entity is Point3d)
                        {
                            var piont = (Point3d)entity;
                            var newpiont = new Point3d(piont.X, piont.Y + 1000, piont.Z);
                            csharp_Delauney.AddPoint(newpiont.X, newpiont.Y);
                        }
                    }
                    var dVertices = csharp_Delauney.GetDVertices();
                    var dTriangles = csharp_Delauney.GetDTriangles();
                    var HowMany = csharp_Delauney.HowMany;
                    db.SetCurrentLayer(db.GetLayer("轮廓线"));
                    DBObjectCollection tdBObjectCollectionLine = new DBObjectCollection();//画地形
                    for (var i = 1; i <= HowMany; i++)
                    {
                        //  g.DrawLine(myPen, Vertex[Triangle[i].vv0].x, Vertex[Triangle[i].vv0].y, Vertex[Triangle[i].vv1].x, Vertex[Triangle[i].vv1].y);
                        var ptA1 = new Point3d(dVertices[dTriangles[i].vv0].x, dVertices[dTriangles[i].vv0].y, 0);
                        var ptA2 = new Point3d(dVertices[dTriangles[i].vv1].x, dVertices[dTriangles[i].vv1].y, 0);
                        var aLine = ptA1.Line(ptA2);
                        tdBObjectCollectionLine.Add(aLine);
                        // g.DrawLine(myPen, Vertex[Triangle[i].vv1].x, Vertex[Triangle[i].vv1].y, Vertex[Triangle[i].vv2].x, Vertex[Triangle[i].vv2].y);
                        var ptB1 = new Point3d(dVertices[dTriangles[i].vv1].x, dVertices[dTriangles[i].vv1].y, 0);
                        var ptB2 = new Point3d(dVertices[dTriangles[i].vv2].x, dVertices[dTriangles[i].vv2].y, 0);
                        var bLine = ptB1.Line(ptB2);
                        tdBObjectCollectionLine.Add(bLine);
                        // g.DrawLine(myPen, Vertex[Triangle[i].vv0].x, Vertex[Triangle[i].vv0].y, Vertex[Triangle[i].vv2].x, Vertex[Triangle[i].vv2].y);
                        var ptC1 = new Point3d(dVertices[dTriangles[i].vv0].x, dVertices[dTriangles[i].vv0].y, 0);
                        var ptC2 = new Point3d(dVertices[dTriangles[i].vv2].x, dVertices[dTriangles[i].vv2].y, 0);
                        var cLine = ptC1.Line(ptC2);
                        tdBObjectCollectionLine.Add(cLine);
                    }

                    db.AddObjectsToModelSpace(tdBObjectCollectionLine);

代码

https://download.csdn.net/download/bosslizhiyong/21454486