概述
本篇文章主要讲述一下分布式数据库中的排序优化算法,之所以叫做优化算法,是因为每种排序算法分别是针对不同的排序场景量身定制的,较基础的全排序有更好的性能。
sort的使用场景除业务本身显示指定order by之外,它还用于group by、distinct、join、union等算子的辅助实现,比如使用merge group by来实现groupby的时候需要下层额外分配一个sort,这部分是优化器生成逻辑执行计划时添加的,实现时与显式的sort无异。
sort在数据库中作为一个算子来实现,是一个需要物化的算子,物化的概念在这里是指需要将下层算子传递上来的数据缓存下来,而不是像一些其它算子拿到一行数据处理完就可以流水线一般一直向上传递,而它需要拿到所有的下层传递上来的数据才能进行本身的排序处理,排好之后才可以再向上层算子吐数据。如此,对于排序的性能影响较大的主要有两个方面,一个是排序本身,一个是深拷贝的过程。
针对这样的性能问题,考虑不同的业务场景,几种优化算法应运而生。本文主要介绍以下两种排序算法:
- topn-sort
- 分布式的多路归并排序
(配图为堆排,[出处http://www.blogjava.net/todayx-org/archive/2012/01/08/368091.html)]
topn-sort
介绍
一条sql秒懂topn-sort的应用场景:
select * from t1 order by c1 limit 10;
topn的问题通常是指从大数据量中获得前n个满足要求的数据,可以是近似的也可以是精确的,近似的算法OceanBase也是有的,在OceanBase里面叫做topk。 这里主要讲精确的前n个,用于order by + limit 的场景,这是比较常用的,用户往往会关注最xx的事情,比如你想知道偷你能量最多是哪几个人。
实现
topn由n大小的堆实现,下层算子吐出来的数据未达到n行数据时,直接放入heap_array中,这里会做深拷贝,直到拿到了n行数据后,创建n大小的堆,小顶还是大顶根据排序要求来定。之后再拿到数据就会去更新这个堆,根据与堆顶数据的一次比较决定是直接丢掉还是放入堆中,直到更新完所有的数据。
以取前n大的数据为例:
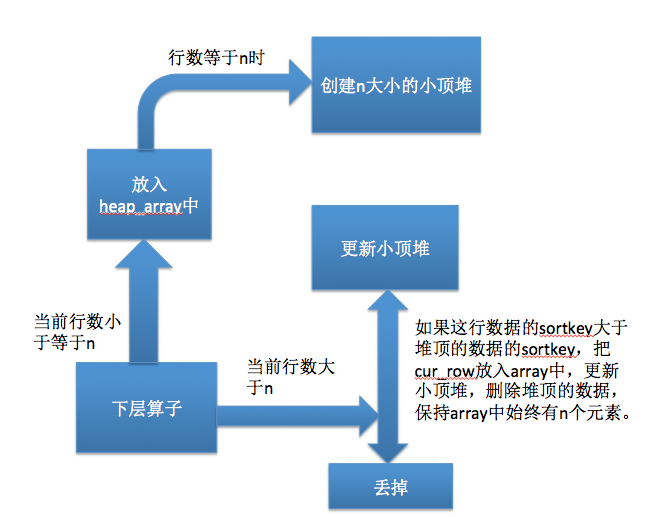
性能提升与不足
- 从算法时间复杂度来看,全排序为NlogN, topn为N1logn, N1最坏等于N。
- topn不需要压缩存,基础全排序使用了压缩存储。数据均匀的情况下,topn只需要部分深拷贝。
分布式的多路归并排序merge-sort
介绍
多路归并排序也被应用于基础排序的外排中,对于数据量比较大内存中放不下的情况,会分成多份放在文件中,向上返回数据时按照多份数据源进行归并。这里的应用场景为分区表的排序,需要每个分区按照键值是有序的,每一个数据源对应一个分区的数据返回。
select * from t1 order by c1;
比如这样的一条简单的sql, t1是分区表,没有merge-sort的情况,需要把每个分区的数据拉上来,做一次全排序。使用merge-sort,如果c1本来就是主键或者存储层走的索引,每个分区原本就是有序的,那么只需要在上层做一次归并排序即可,如果分区无序,可以把order by c1下压到每一个分区去做排序,最后再做一次归并排序,两种情况都会比全排序的性能好。
实现
从中间结果管理器中拉取每一个分区的数据序列化好放在rowstore(可以压缩存储row的一个结构)中,对于每一个分区的数据可以看作一个数据源,每个数据源取一行组成一个k大小的堆,由上层算子驱动,迭代返回堆顶的数据,每返回一行数据,要从对应的数据源中补回一行,重新调整堆。

性能提升
- 需要全排序的情况,分区有序,算法复杂度由NLOGN降到NLOGK, K指分区表的数量;分区无序,由NLOGN到KLOGN/K+NLOGK。上层有limit n时,只需要迭代n次就可以。
- 所有的数据都会在rowstore中存储,所以处理过程中不需要深拷贝,与全排序相比,少了N行深拷贝的时间。
- 没有merge-sort时,做order by的下压是没有意义的,实现merge-sort之后,可以将order by以及limit+order by下压到每个分区去做,某些场景大大减少了数据的拉取和处理。
总结
优化无止境,性能对数据库来讲至关重要,不放过每一个可以优化的性能点,精益求精。路漫漫其修远兮,吾将上下而求索~