hdu_1059(多重背包)

多重背包的讲解：

多重背包问题https://blog.csdn.net/yandaoqiusheng/article/details/84782655

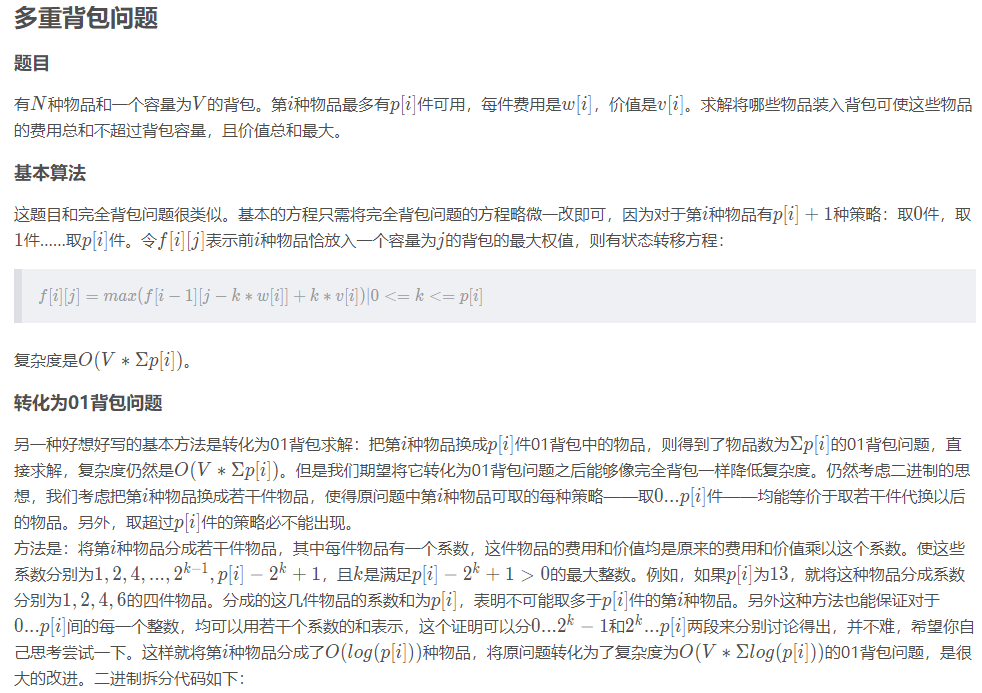
for (int i = 1; i <= n; i++) {
    int num = min(p[i], V / w[i]);
    for (int k = 1; num > 0; k <<= 1) {
        if (k > num) k = num;
        num -= k;
        for (int j = V; j >= w[i] * k; j--)
            f[j] = max(f[j], f[j - w[i] * k] + v[i] * k);
    }
}

本题题解：由于没有空间的限制，只是价值的限制，那么直接考虑用价值作为容量，然后状态定义为在所给物品可以拆分成价值为j的可能性，所有状态除了dp[0] = 0，其他等于-1

状态转移： dp[j] = max(dp[j] , dp[j-k*v[i]]])  k 用上面二分的方法

本题代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int main()
{
    int p[6];
    int cnt = 0;
    while(~scanf("%d%d%d%d%d%d",&p[0],&p[1],&p[2],&p[3],&p[4],&p[5])){
        if(p[0]==0&&p[1]==0&&p[2]==0&&p[3]==0&&p[4]==0&&p[5]==0)
            return 0;
        int V = 0;
        for(int i = 0; i < 6; i++){
            V += p[i]*(i+1);
        }
        if(V%2!=0){
            printf("Collection #%d:
",++cnt);
            printf("Can't be divided.
");
            puts("");
            continue;
        }
        int dp[V/2+1];
        memset(dp,-1,sizeof(dp));
        dp[0] = 0;
        for(int i = 0;i < 6; i++){
            int num = p[i];
            for(int k = 1; num>0 ; k<<=1){
                if(k>num) k = num;
                num -= k;
                for(int j = V/2; j>=k*(i+1); j--){
                    dp[j] = max(dp[j],dp[j-k*(i+1)]);
                }
            }
        }
        /*for(int i = 0; i <= V/2; i++){
            printf("%d ",dp[i]);
        }
        puts("");*/
        if(dp[V/2]==0){
            printf("Collection #%d:
",++cnt);
            printf("Can be divided.
");
            puts("");
        }
        else{
            printf("Collection #%d:
",++cnt);
            printf("Can't be divided.
");
            puts("");
        }
    }
    return 0;
}