最短路径——迪杰斯特拉和弗洛伊德算法

求图的最短路径，是一种常考算法。通常有两种算法：可以参考下面的博客：

https://blog.51cto.com/gelivable/427009

https://blog.csdn.net/zxq2574043697/article/details/9451887

关于迪杰斯特拉算法：

 

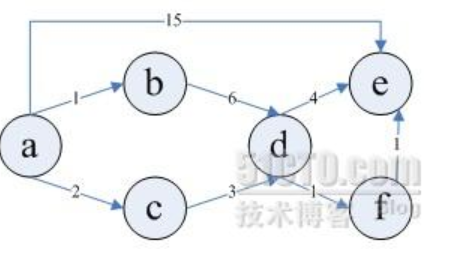
 总结：迪杰斯特拉算法：是求某个点到其他所有点的最短路径，最终得到的是一个距离集合。

2：floyd算法

floyd算法求解的是图中任意两点的最短距离，其得到的是一个距离矩阵：

代码：

#include<iostream>  
#define MAX_VERTEX 100  
#define INFINITE 65535  
using namespace std;
//array   

char vertex_infos[MAX_VERTEX];  
int matrix[MAX_VERTEX][MAX_VERTEX];
int main(){
    for(int i=0;i<MAX_VERTEX;i++){   
        vertex_infos[i]=0;  
        for(int j=0;j<MAX_VERTEX;j++){   
            matrix[i][j]=INFINITE;   
            matrix[i][j]=INFINITE;   
        }
    }  
       
    cout<<"input vertex and side nums:";   
    int num_vertex;   
    int num_side;   
    cin>>num_vertex>>num_side;   
       
    cout<<"input vertex char data:";   
    for(int i=0;i<num_vertex;i++){   
        cin>>vertex_infos[i];   
    }   
       
    for(int i=0;i<num_side;i++){   
        int v1;   
        int v2;   
        int weight;  
        cout<<"input two vertex:";   
        cin>>v1>>v2;   
        cout<<"input weight:";   
        cin>>weight;   
        matrix[v1][v2]=weight;  
        matrix[v2][v1]=weight;  
    }
    cout<<"initial:"<<endl;
        for(int i=0;i<num_vertex;i++){   
        for(int j=0;j<num_vertex;j++){
            cout<<matrix[i][j]<<' ';
        }
        cout<<endl;
    }
    for(int k=1;k<num_vertex;k++){
        for(int i=0;i<num_vertex;i++){
            for(int j=0;j<num_vertex;j++){
                if(i!=j&&matrix[i][k]+matrix[k][j]<matrix[i][j]){
                    matrix[i][j]=matrix[i][k]+matrix[k][j];
                }
            }
        }
    }
    
    cout<<"floyd:"<<endl;
    for(int i=0;i<num_vertex;i++){   
        for(int j=0;j<num_vertex;j++){
            cout<<matrix[i][j]<<' ';
        }
        cout<<endl;
    }  
    system("pause");
    return 0;
}

上图中46-50行就是floyd算法的核心代码部分：matrix[i][j]表示节点i到节点j的最短距离。

关于floyd算法最通俗的两个描述博客：

https://www.cnblogs.com/wangyuliang/p/9216365.html

https://blog.csdn.net/qq_35644234/article/details/60875818?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-3

总结：floyd算法的本质是初始化距离矩阵，然后我们不断去更新这个矩阵。策略是：如果从i到k，再从k到j的距离小于从i到j的距离，那么我们就更新matrix[i][j]=matrix[i][k]+matrix[k][j]。