一、介绍
线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
1、相关性分析
相关性分析是对两个或多个具备相关性元素进行分析,从而衡量两个变量元素之间相关密切程度。
以双变量为例,变量x 和变量y存在三种关系:正线性相关、负线性相关、不是线性相关(可能是曲线相关)
2、衡量相关性程度
为表示两个变量相关性程度,需要引入两个统计量:协方差和相关系数
a、协方差
协方差(Covariance)在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
b、相关系数
简单相关系数又称皮尔逊相关系数或“皮尔逊积矩相关系数”或叫线性相关系数,是指两个定距变量间联系的紧密程度。相关系数可以看作是两个随机变量中得到的样本集向量之间夹角的cos函数。
相关系数是标准化后的协方差,消除了变量变化幅度的影响,表示变量每单位变化的相似程度。

衡量相关性程度最重要的一点是看相关系数:
1、如果相关系数小于0,则为负线性相关,大于0 ,则为正线性相关。
2、相关系数的取值范围为-1之1间,越靠近-1或者1则相关性越强。相关系数在0至0.3或-0.3至0表示相关性较弱,0.3至0.6或-0.6至-0.3表示中等程度相关,0.6至1或-1至-0.6表示变量强相关
3、最佳拟合线
在散点图上绘制一条直线,使得这条直线尽可能多通过数据点,要求出最佳拟合线需要求出回归方程y=a+bx,其中a为截距,b为回归系数,在方程中使得y的实际观察值与每个x相对应的y
的估计值的差距为最小,即通过最小二乘法拟合:
4、评估模型精确度
可以使用决定系数R平方来评估模型精确度
如下图1和图2所示,图2比图1数据集多,点误差平方和比图1大,但这并不能说明图2精确度比图1小:


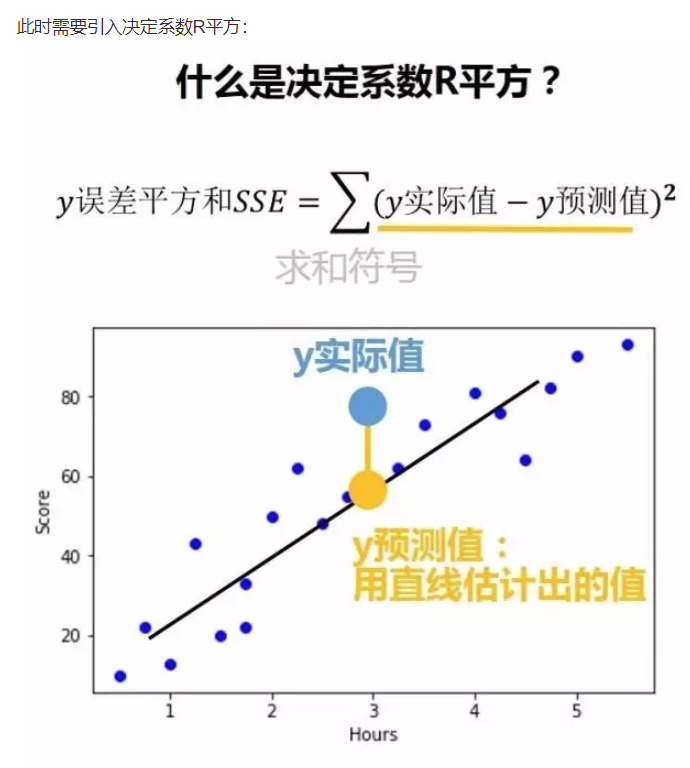


决定系数R平方的两个作用是:
1、描述有多少百分比的y波动可以由回归线来描述(即x的波动变化);
2、决定系数R平方的值越高,回归模型越精确。
二、简单线性回归案例
目的:为了了解学习时间与考试成绩的关系,并通过建立模型,预测考试成绩。
1、首先创建数据集并提取特征和标签:

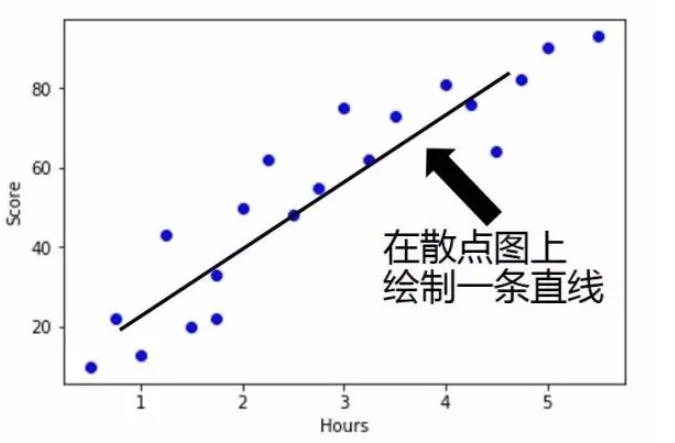
2、通过绘制原始数据的散点图,看看学习时间与考试成绩是否存在线性相关:

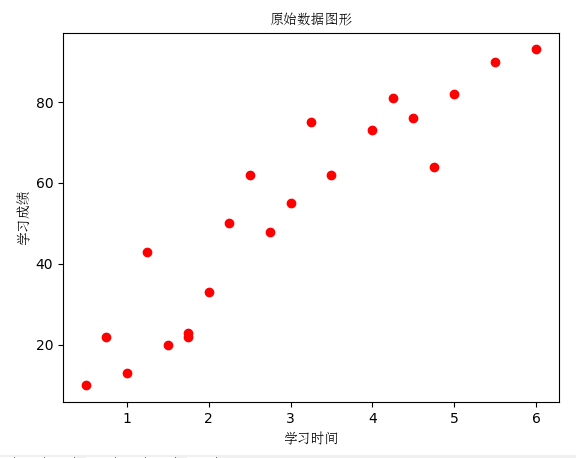
3、通过散点图发现学习时间与考试成绩符合线性回归的模式,为了构建模型先要建立训练数据和测试数据:

4、接着描绘训练数据和测试数据图像:

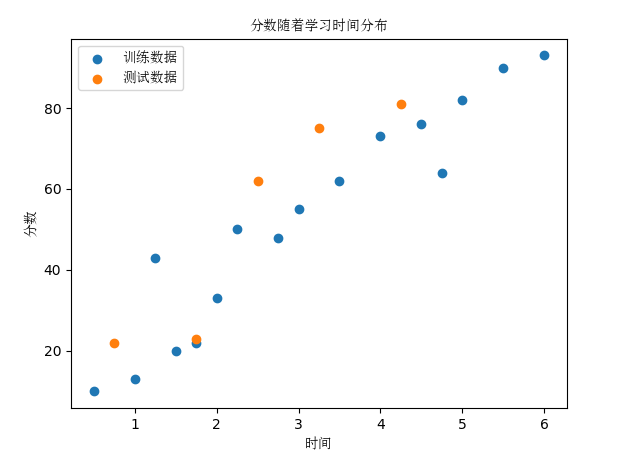
5、构建线性回归模型


6、找出最佳拟合线

7、绘制最佳拟合线的图像


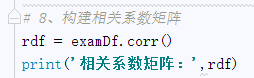
8、构建相关系数矩阵:
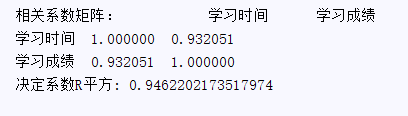
9、求出决定系数R平方:

决定系数R平方: 0.8006634640022074
10、通过测试数据进行评估模型:


结论:通过上面的求出决定系数R平方为0.80066,决定系数R平方接近1,决定系数R平方越大说明学习时间与考试成绩成正线性相关,即学习时间越长,考试成绩越好。
11、全部源码

from sklearn import datasets from sklearn.linear_model import LinearRegression import numpy as np import matplotlib.font_manager as fm # 导入相关模块 from collections import OrderedDict import pandas as pd # 数据集 examDict ={'学习时间':[0.5, 0.75, 1, 1.25,1.5, 1.75,1.75, 2, 2.25, 2.5, 2.75, 3, 3.25, 3.5, 4, 4.25,4.5, 4.75, 5, 5.5,6], '学习成绩':[10, 22, 13, 43, 20, 22, 23, 33, 50, 62, 48, 55,75, 62, 73, 81, 76, 64, 82, 90,93]} examOrderDic = OrderedDict(examDict) examDf = pd.DataFrame(examOrderDic) # print(examDf.head()) # 1、提取特征和标签 exam_X = examDf.loc[:,'学习时间'] exam_Y = examDf.loc[:,'学习成绩'] # ----------------------------------------------------- # 2、建立训练数据和测试数据 import matplotlib.pyplot as plt # 这个主要是为了显示中文 myfont = fm.FontProperties(fname='C:WindowsFontssimsun.ttc') # plt.scatter(exam_X,exam_Y,color='red',label='学习成绩') # plt.title("原始数据图形", fontproperties = myfont) # plt.xlabel('学习时间',fontproperties = myfont) # plt.ylabel('学习成绩',fontproperties = myfont) # plt.show() # ----------------------------------------------------- #3、通过散点图发现学习时间与考试成绩符合线性回归的模式,为了构建模型先要建立训练数据和测试数据 from sklearn.model_selection import train_test_split X_train,X_test,y_train,y_test = train_test_split(exam_X,exam_Y,train_size=0.8) # print('原始数据特征:',exam_X.shape, # '训练数据特征:',X_train.shape, # '测试数据特征:',X_test.shape) # # print('原始数据标签:',exam_Y.shape, # '训练数据标签:',y_train.shape, # '测试数据标签:',y_test.shape) #--------------------------------------------------------- # 4、接着描绘训练数据和测试数据图像: # 散点图 # plt.scatter(X_train,y_train,label='训练数据') # plt.scatter(X_test,y_test,label='测试数据') # plt.legend(loc=2,prop=myfont) # plt.title("分数随着学习时间分布", fontproperties = myfont) # plt.xlabel('时间',fontproperties = myfont) # plt.ylabel('分数',fontproperties = myfont) # # 显示图像 # plt.show() #------------------------------------------------------ # 5、构建线性回归模型 # sklearn要求输入的 特征必须是二维数组的类型,但是因为我们目前只有一个特征, # 所以需要用array.reshape(-1,1)转成二维数组的类型,reshape行的参数是-1,就会根据所给的列数, # 自动按照原始数组的大小形成一个新的的数组 #将训练数据特征转换成二维数组XX行*1列形式 X_train = X_train.values.reshape(-1,1) y_train = y_train.values.reshape(-1,1) #创建线性回归模型 model = LinearRegression() # 训练模型 model.fit(X_train,y_train) # import pickle # # # 保存模型数据 # output_model_file = 'saved_model.pkl' # with open(output_model_file,'wb') as f: # pickle.dump(model,f) # # # # 读取模型数据 # output_model_file = 'saved_model.pkl' # with open(output_model_file,'rb') as f: # model =pickle.load(f) #------------------------------------------------------ # # 6、找出最佳拟合线 # # # 截距 # a = model.intercept_ # # 回归系数 # b= model.coef_ # print('最佳拟合线:截距a=',a,'回归系数b=',b) #------------------------------------------------------ # # 7、绘制最佳拟合线的图像 # # 训练数据散点图 # plt.scatter(X_train,y_train,label='训练数据') # # 训练数据预测值 # y_train_pred = model.predict(X_train) # # 绘制最佳拟合线 # plt.plot(X_train,y_train_pred,color='green',linewidth=3,label='最佳拟合线') # plt.legend(loc=2,prop=myfont) # plt.xlabel('时间',fontproperties = myfont) # plt.ylabel('得分',fontproperties = myfont) # plt.show() #------------------------------------------------------ # 8、构建相关系数矩阵 # rdf = examDf.corr() # print('相关系数矩阵:',rdf) #------------------------------------------------------ # 9、求出决定系数R平方 # X_test = X_test.values.reshape(-1,1) # y_test = y_test.values.reshape(-1,1) # score = model.score(X_test,y_test) # print('决定系数R平方:',score) #------------------------------------------------------ # # 10、通过测试数据进行评估模型 # 绘制最佳拟合线的图像 # 训练数据散点图 plt.scatter(X_train,y_train,color='blue',label='训练数据') # 训练数据预测值 y_train_pred = model.predict(X_train) # 绘制最佳拟合线 plt.plot(X_train,y_train_pred,color='green',linewidth=3,label='最佳拟合线') # 测试数据散点图 plt.scatter(X_test,y_test,color='red',label='测试数据') plt.legend(loc=2,prop=myfont) plt.xlabel('时间',fontproperties = myfont) plt.ylabel('得分',fontproperties = myfont) plt.show() # boston = datasets.load_boston() # # print(boston.target) # print(" ") # sampleRatio = 0.5 # n_samples = len(boston.target) # # print('n_samples='+str(n_samples)) # # print(" ") # sampleBoundary = int(n_samples * sampleRatio) # # print('sampleBoundary='+str(sampleBoundary)) # # print(" ") # shuffleIdx = range(n_samples) # print(shuffleIdx) # # np.random.shuffle(shuffleIdx) # # 训练集的特征和回归值 # train_features = boston.data[shuffleIdx[:sampleBoundary]] # train_targets = boston.target[shuffleIdx[:sampleBoundary]] # # 测试集的特征和回归值 # test_features = boston.data[shuffleIdx[sampleBoundary:]] # test_targets = boston.target[shuffleIdx[sampleBoundary:]] # # # 接下来,获取回归模型,拟合并得到测试集的预测结果: # # lr = LinearRegression() # 需要导入sklearn的linear_model # lr.fit(train_features, train_targets) # 拟合 # y = lr.predict(test_features) # 预测 # # # 最后,把预测结果通过matplotlib画出来: # # plt.plot(y, test_targets, 'rx') # y = ωX # # b-. :直线颜色是蓝色blue,如果显示红色改为:r-.; lw=4:直线的显示粗细 # plt.plot([y.min(), y.max()], [y.min(), y.max()], 'b-.', lw=4) # f(x)=x # plt.ylabel("Predieted Price") # plt.xlabel("Real Price") # plt.show()




