UVa 10382

原题：

n sprinklers are installed in a horizontal strip of grass l meters long and w meters wide. Each sprinkler is installed at the horizontal center line of the strip. For each sprinkler we are given its position as the distance from the left end of the center line and its radius of operation.

What is the minimum number of sprinklers to turn on in order to water the entire strip of grass?

Input

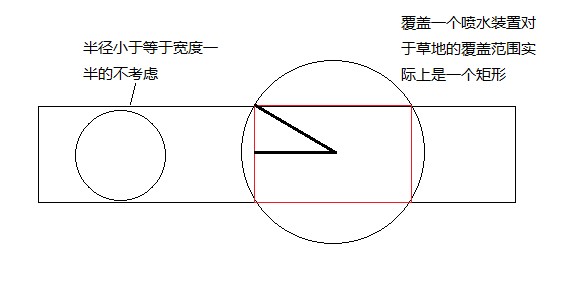
Input consists of a number of cases. The first line for each case contains integer numbers n, l and w with n <= 10000. The next n lines contain two integers giving the position of a sprinkler and its radius of operation. (The picture above illustrates the first case from the sample input.)

Output

For each test case output the minimum number of sprinklers needed to water the entire strip of grass. If it is impossible to water the entire strip output -1.

Sample input

8 20 2

5 3

4 1

1 2

7 2

10 2

13 3

16 2

19 4

3 10 1

3 5

9 3

6 1

3 10 1

5 3

1 1

9 1

 

Sample output

6

2

-1

分析：

这题的关键在于转化

根据这图可以看出，一个喷水装置的有效覆盖范围就是圆中间的那个矩形。所以，在输入的同时，进行预处理，转换成矩形左边的坐标和右边的坐标。 这样，其实就转换成了经典的区间覆盖问题。

代码：

#include<iostream>
#include<cmath>
#include<cstdio>
#include<algorithm>
#define MAXN 10005
using namespace std;
int n, nIndex;
double l, w;


struct Node
{
    double left;
    double right;
    friend bool operator < (const Node&a, const Node&b){
        return a.left < b.left;
    }
}arr[MAXN];

int main(){
    double p, r;
    while (scanf("%d%lf%lf", &n, &l, &w) != EOF){
        nIndex = 0;
        for (int i = 0; i<n; ++i){
            scanf("%lf%lf", &p, &r);
            if (w / 2 >= r)
                continue; //直径小于宽度的不考虑
            double t = sqrt(r*r - w*w / 4.0);
            arr[nIndex].left = p - t;
            arr[nIndex].right = p + t;
            ++nIndex;
        }

        sort(arr, arr + nIndex);
        int cnt = 0;
        double left = 0, right = 0;
        bool flag = false;

        if (arr[0].left <= 0){
            int i = 0;

            while (i < nIndex){

                int j = i;
                while (j<nIndex && left >= arr[j].left){
                    if (arr[j].right > right)
                        right = arr[j].right;
                    ++j;
                }
                if (j == i) break;  // 如果上面的循环体没有执行，说明之后都没有满足的了

                ++cnt;
                left = right;
                i = j;

                if (left >= l){
                    flag = true;
                    break;
                }
            }
        }
        if (flag) printf("%d
", cnt);
        else printf("-1
");
    }
    return 0;
}