聚类分析笔记
部分摘抄自网络
0、聚类分析中距离的定义:
(2) 距离的度量
给定样本 $ x^{(i)} = lbrace x_1^{(i)},x_2^{(i)},,...,x_n^{(i)},
brace 与 x^{(j)} = lbrace x_1^{(j)},x_2^{(j)},,...,x_n^{(j)},
brace ,其中 i,j=1,2,...,m,表示样本数,n表示特征数 $ 。距离的度量方法主要分为以下几种:
(2.1)有序属性距离度量(离散属性 $ lbrace1,2,3
brace $ 或连续属性):
闵可夫斯基距离(Minkowski distance): [ dist_{mk}(x^{(i)},x^{(j)})=(sum_{u=1}^n |x_u^{(i)}-x_u^{(j)}|^p)^{frac{1}{p}} ]
欧氏距离(Euclidean distance),即当 $ p=2 $ 时的闵可夫斯基距离: [ dist_{ed}(x^{(i)},x^{(j)})=||x^{(i)}-x^{(j)}||_2=sqrt{sum_{u=1}^n |x_u^{(i)}-x_u^{(j)}|^2} ]
曼哈顿距离(Manhattan distance),即当 $ p=1 $ 时的闵可夫斯基距离: [ dist_{man}(x^{(i)},x^{(j)})=||x^{(i)}-x^{(j)}||_1=sum_{u=1}^n |x_u^{(i)}-x_u^{(j)}| ]
(2.2)无序属性距离度量(比如{飞机,火车,轮船}):
VDM(Value Difference Metric): [ VDM_p(x_u^{(i)},x_u^{(j)}) = sum_{z=1}^k left|frac{m_{u,x_u^{(i)},z}}{m_{u,x_u^{(i)}}} - frac{m_{u,x_u^{(j)},z}}{m_{u,x_u^{(j)}}}
ight|^p ]
其中 $ m_{u,x_u^{(i)}} $ 表示在属性 $ u $ 上取值为 $ x_u^{(i)} $ 的样本数, $ m_{u,x_u^{(i)},z} $ 表示在第 $ z $ 个样本簇中属性 $ u $ 上取值为 $ x_u^{(i)} $ 的样本数, $ VDM_p(x_u^{(i)},x_u^{(j)}) $ 表示在属性 $ u $ 上两个离散值 $ x_u^{(i)} 与 x_u^{(i)} $ 的 $ VDM $ 距离 。
(2.3)混合属性距离度量,即为有序与无序的结合: [ MinkovDM_p(x^{(i)},x^{(j)}) = left( sum_{u=1}^{n_c} | x_u^{(i)} - x_u^{(j)} | ^p + sum_{u=n_c +1}^n VDM_p (x_u^{(i)},x_u^{(j)})
ight) ^{frac{1}{p}} ]
其中含有 $ n_c $ 个有序属性,与 $ n-n_c $ 个无序属性。
本文数据集为连续属性,因此代码中主要以欧式距离进行距离的度量计算。
1、系统聚类
(1)计算数据集每对元素之间的距离,对应函数为pdistw.
调用格式:Y=pdist(X),Y=pdist(X,’metric’), Y=pdist(X,’distfun’),Y=pdist(X,’minkowski’,p)
说明:X是m*n的矩阵,metric是计算距离的方法选项:
metric=euclidean表示欧式距离(缺省值);
metric=seuclidean表示标准的欧式距离;
metric=mahalanobis表示马氏距离。
distfun是自定义的距离函数,p是minkowski距离计算过程中的幂次,缺省值为2.Y返回大小为m(m-1)/2的距离矩阵,距离排序顺序为(1,2),(1,3),…(m-1,m),Y也称为相似矩阵,可用squareform将其转化为方阵。
(2)对元素进行分类,构成一个系统聚类树,对应函数为linkage.
调用格式:Z=linkage(Y), Z=linkage(Y,’method’)
说明:Y是距离函数,Z是返回系统聚类树,method是采用的算法选项,
如下:method=single表示最短距离(缺省值);
complete表示最长距离;median表示中间距离法;
centroid表示重心法;average表示类平均法;
ward 表示离差平方和法(Ward法)。
(3)确定怎样划分系统聚类树,得到不同的类,对应的函数为cluster.
调用格式:T=cluster(Z,’cutoff’,c),T=cluster(Z,’maxclust’,n)
说明:Z是系统聚类树,为(m-1)*3的矩阵,c是阈值,n是类的最大数目,
maxclust是聚类的选项,cutoff是临界值,决定cluster函数怎样聚类。
例题1 利用系统聚类法对5个变量进行分类。
matlab程序
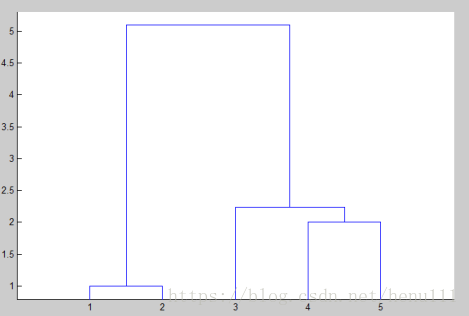
%Matlab运行程序:X=[20,7;18,10;10,5;4,5;4,3];Y=pdist(X);SF=squareform(Y);Z=linkage(Y,’single’);dendrogram(Z);%显示系统聚类树T=cluster(Z,'maxclust',3)例题2
%例2的程序设计:X=[1 1;1 2;6 3;8 2;8 0];Y=pdist(X);SF=squareform(Y);Z=linkage(Y,'single');dendrogram(Z);T=cluster(Z,'maxclust',3)聚类分析案例
根据第三产业国内生产总值的9 项指标,对华东地区6 省1 市进行分类,原始数据如下表:
X=[244.42 412.04 459.63 512.21 160.45 43.51 89.93 48.55 48.63 435.77 724.85 376.04 381.81 210.39 71.82 150.64 23.74 188.28 321.75 665.80 157.94 172.19 147.16 52.44 78.16 10.90 93.50 152.29 258.60 83.42 85.10 75.74 26.75 63.47 5.89 47.02 347.25 332.59 157.32 172.48 115.16 33.80 77.27 8.69 79.01 145.40 143.54 97.40 100.50 43.28 17.71 51.03 5.41 62.03 442.20 665.33 411.89 429.88 115.07 87.45 145.25 21.39 187.77 ]'; Y=pdist(X); SF=squareform(Y); Z=linkage(Y,'average'); dendrogram(Z); T=cluster(Z,'maxclust',5)
2、K均值聚类(Kmeans)
K-means面临的问题以及解决办法:
1.它不能保证找到定位聚类中心的最佳方案,但是它能保证能收敛到某个解决方案(不会无限迭代)。
解决方法:多运行几次K-means,每次初始聚类中心点不同,最后选择方差最小的结果。
2.它无法指出使用多少个类别。在同一个数据集中,例如上图例,选择不同初始类别数获得的最终结果是不同的。
解决方法:首先设类别数为1,然后逐步提高类别数,在每一个类别数都用上述方法,一般情况下,总方差会很快下降,直到到达一个拐点;这意味着再增加一个聚类中心不会显著减少方差,保存此时的聚类数。
MATLAB函数Kmeans(/kmeans)
使用方法:
Idx=Kmeans(X,K)
[Idx,C]=Kmeans(X,K)
[Idx,C,sumD]=Kmeans(X,K)
[Idx,C,sumD,D]=Kmeans(X,K)
[…]=Kmeans(…,’Param1’,Val1,’Param2’,Val2,…)
各输入输出参数介绍:
X: N*P的数据矩阵,N为数据个数,P为单个数据维度
K: 表示将X划分为几类,为整数
Idx: N*1的向量,存储的是每个点的聚类标号
C: K*P的矩阵,存储的是K个聚类质心位置
sumD: 1*K的和向量,存储的是类间所有点与该类质心点距离之和
D: N*K的矩阵,存储的是每个点与所有质心的距离
[…]=Kmeans(…,'Param1',Val1,'Param2',Val2,…)
这其中的参数Param1、Param2等,主要可以设置为如下:
1. ‘Distance’(距离测度)
‘sqEuclidean’ 欧式距离(默认时,采用此距离方式)
‘cityblock’ 绝度误差和,又称:L1
‘cosine’ 针对向量
‘correlation’ 针对有时序关系的值
‘Hamming’ 只针对二进制数据
2. ‘Start’(初始质心位置选择方法)
‘sample’ 从X中随机选取K个质心点
‘uniform’ 根据X的分布范围均匀的随机生成K个质心
‘cluster’ 初始聚类阶段随机选择10%的X的子样本(此方法初始使用’sample’方法)
matrix 提供一K*P的矩阵,作为初始质心位置集合
3. ‘Replicates’(聚类重复次数) 整数
使用案例:
data = [5.0 3.5 1.3 0.3 -1; 5.5 2.6 4.4 1.2 0; 6.7 3.1 5.6 2.4 1; 5.0 3.3 1.4 0.2 -1; 5.9 3.0 5.1 1.8 1; 5.8 2.6 4.0 1.2 0]; [Idx,C,sumD,D]=kmeans(data,3,'dist','sqEuclidean','rep',3)
运行结果:
Idx =
1
3
2
1
2
3
C =
5.0000 3.4000 1.3500 0.2500 -1.0000
6.3000 3.0500 5.3500 2.1000 1.0000
5.6500 2.6000 4.2000 1.2000 0
sumD =
0.0300
0.6300
0.1250
D =
0.0150 25.5350 11.4525
12.0950 3.5550 0.0625
29.6650 0.3150 5.7525
0.0150 24.9650 10.7525
21.4350 0.3150 2.3925
10.2050 4.0850 0.0625
3、聚类效果评价
评价标准:
![clip_image016[6]](https://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104061601542480.png)
假设有M个数据源,C个聚类中心。µc为聚类中心。该公式的意思也就是将每个类中的数据与每个聚类中心做差的平方和,J最小,意味着分割的效果最好。
用matlab自带的工具箱进行聚类效果分析,
data = [0.697 0.460;0.774,0.376;0.634,0.264;0.608,0.318;0.556,0.215;0.403,0.237; 0.481,0.149;0.437,0.211;0.666,0.091;0.243,0.267;0.245,0.057;0.343,0.099; 0.639 0.161;0.657,0.198;0.360,0.370;0.593,0.042;0.719,0.103;0.359,0.188; 0.339,0.241;0.282,0.257;0.748,0.232;0.714,0.346;0.483,0.312;0.478,0.437; 0.525,0.369;0.751,0.489;0.532,0.472;0.473,0.376;0.725,0.445;0.446,0.459;]; rng('default'); % For reproducibility eva = evalclusters(data,'kmeans','CalinskiHarabasz','KList',[1:10]) plot(eva);
类中心个数的评估:
eva= evalclusters(mat,'kmeans','CalinskiHarabasz',...
'klist',[1:6])eva= evalclusters(mat,'linkage','CalinskiHarabasz',...
'klist',[1:6])eva= evalclusters(mat,'gmdistribution','CalinskiHarabasz',...
'klist',[1:6])mat------你自己的要聚类的数据,(n*d)每行是一个样本。
'kmeans'-----这里是聚类算法,kmeans大家都知道。linkage是针对有层次数据的聚类算法,而gmd是高斯混合聚类。
'CalinskiHarabasz'-------是聚类的评价标准,还有另外 三个选项:
'DaviesBouldin''gap''silhouette'
那么,假如你已经用这个算法得到了结果,关键问题就变成了怎么挑选最佳聚类中心数目。
klist-----聚类中心的范围。
挑选聚类中心
同样的数据,不同的评价标准,都是kmeans聚类方式。
‘CalinskiHarabasz(CH)'挑选拐点,所以这张图的聚类中心是20.,为了看不同的同学,我给出代码:
plot(eva.CriterionValues)'DaviesBouldin'最大值点,拐点,所以可以选择20-40之间。